ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Δευ Απρ 05, 2021 12:01 pm
Η απάντηση είναι ΟΧΙ.
Πάρε πίνακα με

χαρακτηριστικό και ελάχιστο.
Αν

τότε

και δεν διαιρεί το χαρακτηριστικό.
Σταύρο, αυτό που ανέβασα ήταν μια προσπάθεια γενίκευσης. Ας δούμε και την παρακάτω περίπτωση:

και για το

ισχύει

. Τότε το χαρακτηριστικό πολυώνυμο του

έχει οπωσδήποτε σαν ρίζες τους

;
Σημείωση: Σε αυτήν την περίπτωση ο βαθμός του πολυωνύμου

είναι
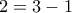
. Μπορούμε να γενικεύσουμε για οποιαδήποτε διάσταση; Δηλαδή
Έστω πίνακας

και ένα πολυώνυμο
![p(x)\in\mathbb{R}[x] p(x)\in\mathbb{R}[x]](/forum/ext/geomar/texintegr/latexrender/pictures/13472a03624bd2dad6cd3bcaa83fc90e.png)
βαθμού

με όλες τις

ρίζες του να είναι διακριτοί πραγματικοί αριθμοί. Αν

, τότε πάντοτε το

διαιρεί το χαρακτηριστικό πολυώνυμο του

;
 και ένα πολυώνυμο
και ένα πολυώνυμο ![p(x)\in\mathbb{R}[x] p(x)\in\mathbb{R}[x]](/forum/ext/geomar/texintegr/latexrender/pictures/13472a03624bd2dad6cd3bcaa83fc90e.png) βαθμού
βαθμού  με όλες τις ρίζες του να είναι απλές και διακριτοί πραγματικοί αριθμοί. Αν
με όλες τις ρίζες του να είναι απλές και διακριτοί πραγματικοί αριθμοί. Αν  , τότε πάντοτε το
, τότε πάντοτε το  διαιρεί το χαρακτηριστικό πολυώνυμο του
διαιρεί το χαρακτηριστικό πολυώνυμο του  ;
; είναι διακριτές, αυτές είναι απλές.
είναι διακριτές, αυτές είναι απλές.




 και για το
και για το  ισχύει
ισχύει  ;
; 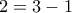 . Μπορούμε να γενικεύσουμε για οποιαδήποτε διάσταση; Δηλαδή
. Μπορούμε να γενικεύσουμε για οποιαδήποτε διάσταση; Δηλαδή με όλες τις
με όλες τις 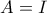 και
και 