Πρόβλημα: Έστω
 ένας δακτύλιος ο οποίος έχει ένα στοιχείο
ένας δακτύλιος ο οποίος έχει ένα στοιχείο  ώστε
ώστε 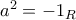 .
.Να αποδειχθεί ότι υπάρχει μοναδικός δακτύλιος ομομορφισμών
![\varphi : \mathbb{Z} [ i ] \longrightarrow R \varphi : \mathbb{Z} [ i ] \longrightarrow R](/forum/ext/geomar/texintegr/latexrender/pictures/6d0a65f16c0596ce4796ddfafc826a5b.png) έτσι ώστε
έτσι ώστε 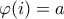 .
.Σημειώνουμε ότι:
![\mathbb{Z} [ i ] \mathbb{Z} [ i ]](/forum/ext/geomar/texintegr/latexrender/pictures/f87010a867148962faa2ab05751ef7f3.png) συμβολίζουμε τον δακτύλιο των ακεραίων του Gauss, όπου
συμβολίζουμε τον δακτύλιο των ακεραίων του Gauss, όπου ![\mathbb{Z} [ i ] = \big \{ a + b i : a , b \in \mathbb{Z} \big \} \mathbb{Z} [ i ] = \big \{ a + b i : a , b \in \mathbb{Z} \big \}](/forum/ext/geomar/texintegr/latexrender/pictures/bb70c5e9e9fd6305651c7f1d1fb0347c.png) με
με 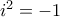 η φανταστική μόναδα
η φανταστική μόναδαή διαφορετικά
είναι ο δακτύλιος πηλίκο
![\mathbb{Z} [ x ] / < x^{2} + 1 > \cong \mathbb{Z} [ i ] \mathbb{Z} [ x ] / < x^{2} + 1 > \cong \mathbb{Z} [ i ]](/forum/ext/geomar/texintegr/latexrender/pictures/56be1d9f63d11bbce6f6b5d7a85efe6c.png) , όπου
, όπου ![\mathbb{Z} [ x ] \mathbb{Z} [ x ]](/forum/ext/geomar/texintegr/latexrender/pictures/927c9ea238b830569537a8d61e08b64d.png) είναι ο δακτύλιος των πολυωνύμων με ακέραιους συντελεστές και
είναι ο δακτύλιος των πολυωνύμων με ακέραιους συντελεστές και ![< x^{2} + 1 > = \big \{ (x^{2} + 1) f ( x ) : f ( x ) \in \mathbb{Z} [ x ] \big \} < x^{2} + 1 > = \big \{ (x^{2} + 1) f ( x ) : f ( x ) \in \mathbb{Z} [ x ] \big \}](/forum/ext/geomar/texintegr/latexrender/pictures/d80280c79fd69df9152d62e61e07c51d.png) το ιδεώδες που παράγεται από το πολυώνμο
το ιδεώδες που παράγεται από το πολυώνμο 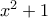 .
.Σας παρακαλώ μπορείτε να με βοηθήσετε με την λύση, σας ευχαριστώ πολύ.

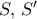 είναι δύο μοναδιαίοι προσεταιριστικοί δακτύλιοι τότε για κάθε μοναδιαίο ομομορφισμό
είναι δύο μοναδιαίοι προσεταιριστικοί δακτύλιοι τότε για κάθε μοναδιαίο ομομορφισμό 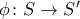 ισχύει
ισχύει 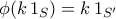 για κάθε
για κάθε 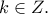 Αυτή η σχέση προκύπτει άμεσα από το γεγονός ότι
Αυτή η σχέση προκύπτει άμεσα από το γεγονός ότι 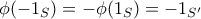 και από την
και από την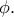 Έπεται λοιπόν ότι η
Έπεται λοιπόν ότι η  είναι
είναι  -γραμμική καθώς
-γραμμική καθώς 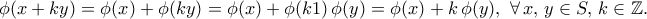
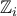 σαν
σαν  και
και  .
. 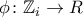 καθορίζεται πλήρως και μοναδικά από τις τιμές
καθορίζεται πλήρως και μοναδικά από τις τιμές 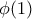 και
και 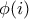 .
.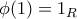 και
και 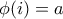 και επεκτείνοντας
και επεκτείνοντας