Σελίδα 1 από 136
Μαθηματικοί διαγωνισμοί - Γυμνάσιο
Δημοσιεύτηκε: Τρί Μάιος 17, 2011 11:02 pm
από ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
Επειδή πολλοί μαθητές του Γυμνασίου ενδιαφέρονται για τους διαγωνισμούς που γίνονται κάθε χρόνο, αλλά δεν έχουν αποκτήσει την εμπειρία σχετικά με τα θέματα που μπαίνουν, προτείνω να ξεκινήσουμε να βάζουμε θέματα που είτε έχουν τεθεί παλιά ή είναι παρόμοιου επιπέδου αρχίζοντας με εύκολα, ώστε να μπουν σιγά σιγά στο νόημα οι αρχάριοι αλλά ταλαντούχοι μαθητές. Επίσης προτείνω να αφήνουμε για 5 ημέρες το κάθε θέμα ώστε να απαντηθεί από τους μαθητές και αν όχι να γράφουμε εμείς μια λύση (ή περισσότερες αν υπάρχουν) .
Ξεκινάω με μια άσκηση που έχει τεθεί παλιά από την ΕΜΕ στην Β Γυμνασίου:
ΑΣΚΗΣΗ 1: Να υπολογίσετε τις παραστάσεις:
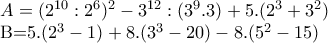 (Ας το αφήσουμε να απαντηθεί από μαθητές μέχρι 22-5-2011)
(Ας το αφήσουμε να απαντηθεί από μαθητές μέχρι 22-5-2011)
Ιωάννου Δημήτρης
Re: Μαθηματικοί διαγωνισμοί
Δημοσιεύτηκε: Τετ Μάιος 18, 2011 10:25 am
από ΑΡΣΕΝΟΗ
Re: Μαθηματικοί διαγωνισμοί
Δημοσιεύτηκε: Τετ Μάιος 18, 2011 11:32 am
από sokratis lyras
Αρσενόη έχεις κάνει ένα λάθος στο αποτέλεσμα του Α..για κοίταξέ το πάλι.
Re: Μαθηματικοί διαγωνισμοί
Δημοσιεύτηκε: Τετ Μάιος 18, 2011 1:12 pm
από ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
Αρσενόη, ένα μεγάλο μπράβο, που παρόλο ότι γράφεις άλλα μαθήματα, βρίσκεις τον χρόνο και ασχολείσαι και με τέτοια θέματα.
Συνεχίζω με δύο ακόμα ασκήσεις. (Η μία έχει τεθεί σε διαγωνισμό της ΕΜΕ στην Γ Γυμνασίου)
ΑΣΚΗΣΗ 2.: Να βρείτε την τιμή της παράστασης:
 ΑΣΚΗΣΗ 3.
ΑΣΚΗΣΗ 3.: Αν

, να βρείτε την τιμή της παράστασης

Re: Μαθηματικοί διαγωνισμοί
Δημοσιεύτηκε: Τετ Μάιος 18, 2011 6:02 pm
από Γιώτα
ΔΗΜΗΤΡΗΣ έγραψε:ΑΣΚΗΣΗ 2.: Να βρείτε την τιμή της παράστασης:

Το 2n είναι σίγουρα άρτιος αριθμός οπότε την πρώτη φορά προσθέτοντας του το 2011 που είναι περιττός το άθροισμα τους γίνεται και αυτό περιττός αριθμός, άρα το
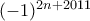
θα γίνει -1.
Εφόσον το 2n+2011 είναι περιττός το 2n+2012 είναι άρτιος άρα το

γίνεται 1.
Άρα έχω:

Re: Μαθηματικοί διαγωνισμοί
Δημοσιεύτηκε: Τετ Μάιος 18, 2011 6:39 pm
από Γιώτα
ΔΗΜΗΤΡΗΣ έγραψε:ΑΣΚΗΣΗ 3.: Αν

, να βρείτε την τιμή της παράστασης

Θα ξεκινήσω αναλύοντας μόνο του το κλάσμα.
![\displaystyle{\frac{6-10x+8x-2y-6}{3[(x-z)+(y+z)]}=\frac{-2(x+y)}{3(x+y)}=-\frac{2}{3}} \displaystyle{\frac{6-10x+8x-2y-6}{3[(x-z)+(y+z)]}=\frac{-2(x+y)}{3(x+y)}=-\frac{2}{3}}](/forum/ext/geomar/texintegr/latexrender/pictures/48816376b1d8c88f1218dac792073e37.png)
Άρα τώρα έχω:

Re: Μαθηματικοί διαγωνισμοί
Δημοσιεύτηκε: Τετ Μάιος 18, 2011 8:39 pm
από ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
Μπράβο Γιώτα.
Συνεχίζω με δύο ακόμα θέματα που έχουν τεθεί σε διαγωνισμό της ΕΜΕ στην Β και στην Γ Γυμνασίου:
ΑΣΚΗΣΗ 4.: Δίνονται οι αριθμοί:

όπου

άρτιος φυσικός αριθμός.
Να συγκριθούν οι αριθμοί
 ΑΣΚΗΣΗ 5.
ΑΣΚΗΣΗ 5. Αν
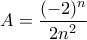
,

, όπου

θετικός ακέραιος, να βρεθεί ποιος από τους αριθμούς

και

είναι μεγαλύτερος.
Re: Μαθηματικοί διαγωνισμοί
Δημοσιεύτηκε: Τετ Μάιος 18, 2011 10:03 pm
από Γιώτα
ΔΗΜΗΤΡΗΣ έγραψε:
ΑΣΚΗΣΗ 4.: Δίνονται οι αριθμοί:

όπου

άρτιος φυσικός αριθμός.
Να συγκριθούν οι αριθμοί



Αρα ο αριθμός

αφού

είναι άρτιος.
Αρα
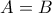
ΔΗΜΗΤΡΗΣ έγραψε:ΑΣΚΗΣΗ 5. Αν
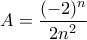
,

, όπου

θετικός ακέραιος, να βρεθεί ποιος από τους αριθμούς

και

είναι μεγαλύτερος.
Αφού τα δυο κλάσματα έχουν τον ίδιο αριθμητή το μεγαλύτερο είναι αυτό με το μικρότερο παρονομαστή. Άρα πρέπει να συγκρίνω το
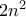
και

.
Το
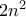
είναι σαφώς μικρότερο άρα
 Έκανα λάθος.
Έκανα λάθος.
Aυτό ισχύει μόνο όταν το

είναι άρτιος. Οταν το

είναι περιττός το πρόσημο είναι μείον οποτε μεγαλύτερος είναι ο

. Το
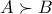
ισχύει μόνο για τις απόλυτες τιμές.
Re: Μαθηματικοί διαγωνισμοί
Δημοσιεύτηκε: Πέμ Μάιος 19, 2011 3:51 am
από ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
Ωραίες λύσεις!!
Πριν συνεχίσω τις υπόλοιπες ασκήσεις, θα ήθελα να παραθέσω μερικές παρατηρήσεις για να ανεβάσουμε λίγο τον πήχη.
(α) Αν ένας αριθμός λήγει σε 0 ή 1 ή 5 ή 6, τότε κάθε δύναμη που έχει βάση τον αριθμό αυτό θα λήγει επίσης σε 0 ή 1ή 5 ή 6 αντίστοιχα.
(β) Ένας φυσικός αριθμός που λήγει σε 2 ή 3 ή 7 ή 8, δεν μπορεί να είναι τετράγωνος (δηλ. δεν μπορεί να πάρει την μορφή τετραγώνου φυσικού αριθμού)
Από τις δύο επόμενες ασκήσεις, η μία έχει τεθεί σε διαγωνισμό της ΕΜΕ για την Γ Γυμνασίου.
ΑΣΚΗΣΗ 6: Αν
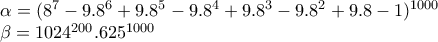
να συγκρίνετε τους αριθμούς
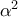
και
 ΑΣΚΗΣΗ 7:
ΑΣΚΗΣΗ 7: Να βρείτε το ψηφίο των μονάδων του αριθμού

Re: Μαθηματικοί διαγωνισμοί
Δημοσιεύτηκε: Πέμ Μάιος 19, 2011 9:06 am
από ΑΡΣΕΝΟΗ
Καλημέρα...
ΔΗΜΗΤΡΗΣ έγραψε:ΑΣΚΗΣΗ 6: Αν
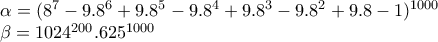
να συγκρίνετε τους αριθμούς
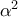
και


![\dispaystyle\ [8^{7}-(8+1){\cdot8^{6}+(8+1){\cdot8^{5}-(8+1) {\cdot 8^{4}+(8+1){\cdot 8^{3}-(8+1){\cdot8^{2}+(8+1){\cdot8-1]^{1000}= \dispaystyle\ [8^{7}-(8+1){\cdot8^{6}+(8+1){\cdot8^{5}-(8+1) {\cdot 8^{4}+(8+1){\cdot 8^{3}-(8+1){\cdot8^{2}+(8+1){\cdot8-1]^{1000}=](/forum/ext/geomar/texintegr/latexrender/pictures/2d730391ae280e2f2db8352dec3836b3.png)


Άρα

Επομένως

ΔΗΜΗΤΡΗΣ έγραψε:ΑΣΚΗΣΗ 7: Να βρείτε το ψηφίο των μονάδων του αριθμού

Τον αριθμό
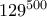
μπορούμε να τον γράψουμε ώς

. Ο

λήγει σε 1 άρα οποιαδήποτε δύναμη του θα λήγει σε 1.Άρα ο αριθμός
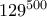
λήγει σε 1.
Re: Μαθηματικοί διαγωνισμοί
Δημοσιεύτηκε: Πέμ Μάιος 19, 2011 10:10 am
από ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
Ωραίες οι λύσεις. ( Το γιατί ο αριθμός b είναι ο μεγαλύτερος, το αφήνω να το ξανασκεφτείς όταν έχεις χρόνο. Είναι πολύ εύκολο).
Συνεχίζω (όσο εσείς λύνετε) με δύο ακόμα ασκήσεις που η μία έχει τεθεί σε διαγωνισμό της ΕΜΕ για την Γ ΄Γυμνασίου:
ΑΣΚΗΣΗ 8:
Να αποδείξετε ότι ο αριθμός:

δεν είναι τέλειο τετράγωνο (ακεραίου)
ΑΣΚΗΣΗ 9.:
Να βρεθεί το ψηφίο των μονάδων του αριθμού :
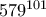
Re: Μαθηματικοί διαγωνισμοί
Δημοσιεύτηκε: Πέμ Μάιος 19, 2011 11:45 am
από Γιώτα
ΔΗΜΗΤΡΗΣ έγραψε:
ΑΣΚΗΣΗ 8:
Να αποδείξετε ότι ο αριθμός:

δεν είναι τέλειο τετράγωνο (ακεραίου)
Τον αριθμό Α μπορώ να τον γράψω και με τη μορφή:
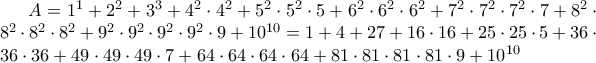
Άρα το τελευταίο ψηφίο του Α είναι

που σημαίνει ότι σίγουρα δεν είναι τέλειο τετράγωνο κανενός ακέραιου αριθμού.
Re: Μαθηματικοί διαγωνισμοί
Δημοσιεύτηκε: Πέμ Μάιος 19, 2011 12:04 pm
από Γιώτα
ΔΗΜΗΤΡΗΣ έγραψε:ΑΣΚΗΣΗ 9.:
Να βρεθεί το ψηφίο των μονάδων του αριθμού :
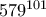
Το ψηφίο των μονάδων του

είναι ίσο με:

Re: Μαθηματικοί διαγωνισμοί
Δημοσιεύτηκε: Πέμ Μάιος 19, 2011 2:46 pm
από T-Rex
ΔΗΜΗΤΡΗΣ έγραψε:ΑΣΚΗΣΗ 7 Να βρείτε το ψηφίο των μονάδων του αριθμού

επειδη το 129 τελειώνει σε 9 οταν πολλαπλασιάζουμε τα εννιαρια περνουμε 1 αν τα εννιαρια ειναι αρτιος αριθμος και 9 αν τα
εννιαρια ειναι περιτος αριθμος
π.χ 9.9.=81 81.9=729 729.9=6561
εδω το 129 το έχουμε 500ιες φορες αρά ο αριθμός

τελειώνει σε 1
Re: Μαθηματικοί διαγωνισμοί
Δημοσιεύτηκε: Πέμ Μάιος 19, 2011 3:44 pm
από ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
Ένα μπράβο και στο μικρό "αστεράκι" του mathematica, T-rex.
Από τις επόμενες δύο ασκήσεις που ακολουθούν, η μία έχει τεθεί σε διαγωνισμό της ΕΜΕ για την Γ Γυμνασίου
ΑΣΚΗΣΗ 10:
Να εξετάσετε αν ο αριθμός

διαιρείται
(α) με το 2
(β) με το 5
ΑΣΚΗΣΗ 11:
Οι ακέραιοι

και

είναι ανάλογοι προς τον αριθμητή και τον παρονομαστή αντίστοιχα του κλάσματος που προκύπτει από την μετατροπή σε κλασματική μορφή του δεκαδικού περιοδικού αριθμού α=4,333...
Να υπολογίσετε την τιμή της παράστασης:

Re: Μαθηματικοί διαγωνισμοί
Δημοσιεύτηκε: Πέμ Μάιος 19, 2011 4:28 pm
από S.E.Louridas
Επειδή ο ΔΗΜΗΤΡΗΣ ξεκίνησε μία πολύ ωραία παρέμβαση ουσίας κόντρα στις λέξεις και επί του πρακτέου, θα προτείνω μία άσκηση από τις σημειώσεις του προπονητικού team της Εθνικής Βουλγαρίας για Juniors υπό τον καθηγητή Ivan Tonov.
ΑΣΚΗΣΗ 12 :
Να υπολογιστεί το ελάχιστο της παράστασης

προσδιορίζοντας ταυτόχρονα και τις τιμές των

για τις οποίες το έχουμε.
S.E.Louridas
Re: Μαθηματικοί διαγωνισμοί
Δημοσιεύτηκε: Πέμ Μάιος 19, 2011 4:44 pm
από ΑΡΣΕΝΟΗ
ΔΗΜΗΤΡΗΣ έγραψε:ΑΣΚΗΣΗ 10:
Να εξετάσετε αν ο αριθμός

διαιρείται
(α) με το 2
(β) με το 5
Καλησπέρα...
Ο αριθμός
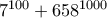
λήγει:
Ο

μπορεί να γραφτεί ώς:

.Το

λήγει σε 1 άρα όλος ο αριθμός θα λήγει σε 1
Ο αριθμός
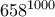
μπορεί να γραφτεί ώς:

.το

λήγει σε 6, άρα όλος ο αριθμός θα λήγει σε 6.
Τέλος: 6+1=7 άρα όλος αυτός ο αριθμός θα λήγει σε 7.Το 7 όμως δε διαιρεί ούτε το 2 ούτε το 5.

Re: Μαθηματικοί διαγωνισμοί
Δημοσιεύτηκε: Πέμ Μάιος 19, 2011 4:53 pm
από Eagle
S.E.Louridas έγραψε:
ΑΣΚΗΣΗ 12.
« Να υπολογιστεί το ελάχιστο της παράστασης

προσδιορίζοντας ταυτόχρονα και τις τιμές των x, y για τις οποίες το έχουμε»
S.E.Louridas
Λοιπόν ας ονομάσουμε Α την παράσταση

.Έτσι

.Συνεπώς η ελάχιστη τιμή της παράστασης είναι το 0 και λαμβάνεται όταν

και όταν

,δηλαδή όταν
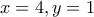
Re: Μαθηματικοί διαγωνισμοί
Δημοσιεύτηκε: Πέμ Μάιος 19, 2011 4:58 pm
από S.E.Louridas
ΑΣΚΗΣΗ 13 : (Από την ίδια πηγή)
Έστω Μ,Ν τα μέσα των πλευρών DC, AB ενός τετράπλευρου ABCD.
Υπολογίστε την τιμή της παράστασης:
 (*)
(*) όταν έχουμε ευθύγραμμο σχήμα μέσα σε παρένθεση εννοούμε το εμβαδόν του.
S.E.Louridas
Re: Μαθηματικοί διαγωνισμοί
Δημοσιεύτηκε: Πέμ Μάιος 19, 2011 5:10 pm
από S.E.Louridas
ΑΣΚΗΣΗ 14 : (Ομοίως από την ίδια πηγή)
Έστω

Να αποδειχθεί ότι :

S.E.Louridas
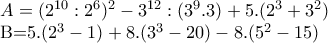
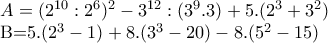
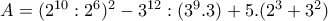

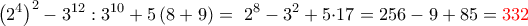
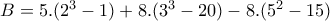




 , να βρείτε την τιμή της παράστασης
, να βρείτε την τιμή της παράστασης 
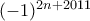 θα γίνει -1.
θα γίνει -1.  γίνεται 1.
γίνεται 1.
![\displaystyle{\frac{6-10x+8x-2y-6}{3[(x-z)+(y+z)]}=\frac{-2(x+y)}{3(x+y)}=-\frac{2}{3}} \displaystyle{\frac{6-10x+8x-2y-6}{3[(x-z)+(y+z)]}=\frac{-2(x+y)}{3(x+y)}=-\frac{2}{3}}](/forum/ext/geomar/texintegr/latexrender/pictures/48816376b1d8c88f1218dac792073e37.png)

 όπου
όπου  άρτιος φυσικός αριθμός.
άρτιος φυσικός αριθμός.
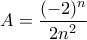 ,
, , όπου
, όπου  και
και  είναι μεγαλύτερος.
είναι μεγαλύτερος.

 αφού
αφού 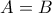
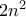 και
και  .
.
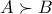 ισχύει μόνο για τις απόλυτες τιμές.
ισχύει μόνο για τις απόλυτες τιμές.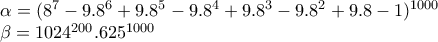
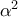 και
και 


![\dispaystyle\ [8^{7}-(8+1){\cdot8^{6}+(8+1){\cdot8^{5}-(8+1) {\cdot 8^{4}+(8+1){\cdot 8^{3}-(8+1){\cdot8^{2}+(8+1){\cdot8-1]^{1000}= \dispaystyle\ [8^{7}-(8+1){\cdot8^{6}+(8+1){\cdot8^{5}-(8+1) {\cdot 8^{4}+(8+1){\cdot 8^{3}-(8+1){\cdot8^{2}+(8+1){\cdot8-1]^{1000}=](/forum/ext/geomar/texintegr/latexrender/pictures/2d730391ae280e2f2db8352dec3836b3.png)




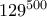 μπορούμε να τον γράψουμε ώς
μπορούμε να τον γράψουμε ώς  . Ο
. Ο  λήγει σε 1 άρα οποιαδήποτε δύναμη του θα λήγει σε 1.Άρα ο αριθμός
λήγει σε 1 άρα οποιαδήποτε δύναμη του θα λήγει σε 1.Άρα ο αριθμός  δεν είναι τέλειο τετράγωνο (ακεραίου)
δεν είναι τέλειο τετράγωνο (ακεραίου)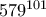
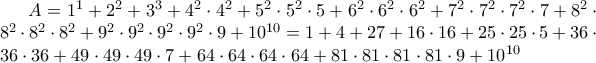
 που σημαίνει ότι σίγουρα δεν είναι τέλειο τετράγωνο κανενός ακέραιου αριθμού.
που σημαίνει ότι σίγουρα δεν είναι τέλειο τετράγωνο κανενός ακέραιου αριθμού. είναι ίσο με:
είναι ίσο με:
 τελειώνει σε 1
τελειώνει σε 1 διαιρείται
διαιρείται  και
και  είναι ανάλογοι προς τον αριθμητή και τον παρονομαστή αντίστοιχα του κλάσματος που προκύπτει από την μετατροπή σε κλασματική μορφή του δεκαδικού περιοδικού αριθμού α=4,333...
είναι ανάλογοι προς τον αριθμητή και τον παρονομαστή αντίστοιχα του κλάσματος που προκύπτει από την μετατροπή σε κλασματική μορφή του δεκαδικού περιοδικού αριθμού α=4,333...

 για τις οποίες το έχουμε.
για τις οποίες το έχουμε.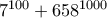 λήγει:
λήγει: μπορεί να γραφτεί ώς:
μπορεί να γραφτεί ώς:  .Το
.Το  λήγει σε 1 άρα όλος ο αριθμός θα λήγει σε 1
λήγει σε 1 άρα όλος ο αριθμός θα λήγει σε 1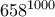 μπορεί να γραφτεί ώς:
μπορεί να γραφτεί ώς:  .το
.το  λήγει σε 6, άρα όλος ο αριθμός θα λήγει σε 6.
λήγει σε 6, άρα όλος ο αριθμός θα λήγει σε 6. .Έτσι
.Έτσι  .Συνεπώς η ελάχιστη τιμή της παράστασης είναι το 0 και λαμβάνεται όταν
.Συνεπώς η ελάχιστη τιμή της παράστασης είναι το 0 και λαμβάνεται όταν  και όταν
και όταν  ,δηλαδή όταν
,δηλαδή όταν