 θετικοί , να δείξετε ότι :
θετικοί , να δείξετε ότι : 
Συντονιστές: cretanman, Demetres, polysot, socrates, silouan
orestis26 έγραψε:Ανθετικοί , να δείξετε ότι :

 που ισχύει.
που ισχύει. λεπτά . Άρα , επί
λεπτά . Άρα , επί  λεπτά έκανες πράξεις!(
λεπτά έκανες πράξεις!( Μετά από 4 χρόνια ας την δούμε και χωρίς πράξεις
 οπότε γίνεται
οπότε γίνεται  .
. αρκεί
αρκεί 


 και
και 

 θέλουμε να δείξουμε ότι
θέλουμε να δείξουμε ότι 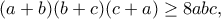
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες