 , ο αριθμός
, ο αριθμός  είναι τέλειο τετράγωνο ;
είναι τέλειο τετράγωνο ;Συντονιστές: cretanman, Demetres, polysot, socrates, silouan
 , ο αριθμός
, ο αριθμός  είναι τέλειο τετράγωνο ;
είναι τέλειο τετράγωνο ; δεν έχουμε λύσεις. Εστω τώρα
δεν έχουμε λύσεις. Εστω τώρα  . Είναι:
. Είναι:
 . Συνεπώς για να είναι το
. Συνεπώς για να είναι το  τέλειο τετράγωνο πρέπει το
τέλειο τετράγωνο πρέπει το  τέλειο τετραγωνο.
τέλειο τετραγωνο. . Για
. Για  δεν έχουμε λύσεις. Εστω τώρα
δεν έχουμε λύσεις. Εστω τώρα  . Εχουμε:
. Εχουμε: . Αρα
. Αρα  . Εχουμε:
. Εχουμε:  . Για
. Για 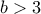 δεν έχουμε λύσεις και μετά με δοκιμές εύκολα παίρνουμε ότι
δεν έχουμε λύσεις και μετά με δοκιμές εύκολα παίρνουμε ότι  ή
ή  ή
ή  .
. 
 Οι αντίστοιχες τιμές του
Οι αντίστοιχες τιμές του  είναι οι
είναι οι 
 οι
οι  λήγουν σε "απαγορευμένο" ψηφίο.
λήγουν σε "απαγορευμένο" ψηφίο. οι
οι  λήγουν σε ένα μηδέν, άρα διαιρούνται από το
λήγουν σε ένα μηδέν, άρα διαιρούνται από το  , αλλά όχι από το
, αλλά όχι από το 
 ο
ο  διαιρείται από το
διαιρείται από το  , αλλά όχι από το
, αλλά όχι από το 
 ο
ο  διαιρείται από το
διαιρείται από το  , αλλά όχι από το
, αλλά όχι από το 
 ο
ο 
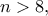 Τότε
Τότε
 δηλαδή μόνο αν υπάρχει θετικός ακέραιος
δηλαδή μόνο αν υπάρχει θετικός ακέραιος  ώστε
ώστε
 με
με  ώστε
ώστε 
 Αν
Αν  το αριστερό μέλος είναι πολλαπλάσιο του
το αριστερό μέλος είναι πολλαπλάσιο του  , ενώ το δεξί όχι. Άρα
, ενώ το δεξί όχι. Άρα  ( το μηδε΄ν απορρίπτεται εύκολα).
( το μηδε΄ν απορρίπτεται εύκολα). και τελικά
και τελικά 


 και
και  , επομένως
, επομένως  , συνεπώς προκύπτει εύκολα ότι
, συνεπώς προκύπτει εύκολα ότι  και επίσης αναγκαστικά
και επίσης αναγκαστικά  , γιατί αν ήταν παραπάνω, η διαφορά θα ήταν μεγαλύτερη του
, γιατί αν ήταν παραπάνω, η διαφορά θα ήταν μεγαλύτερη του  . Άρα
. Άρα 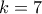 ,
,  και
και  . Άρα
. Άρα  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες