Demetres έγραψε:Να δειχθεί ότι υπάρχουν άπειροι πρώτοι με αυτήν την ιδιότητα.
Για να το δούμε για να μην ξεχαστεί. Η ιδέα είναι να βρούμε άπειρους πρώτους έτσι ώστε το 2 και το 3 να είναι τετραγωνικά κατάλοιπα αλλά το -1 να μην είναι.(*)
Τότε έχουμε το ζητούμενο γιατί η ισοτιμία γράφεται

. Αφού τα 2 και 3 είναι τετραγωνικά κατάλοιπα, γράφουμε

αλλά αν

είναι τέτοιος ώστε

έχουμε ότι

το οποίο είναι άτοπο γιατί το -1 δεν είναι τετραγωνικό κατάλοιπο.
Ας αποδείξουμε τώρα ότι υπάρχουν άπειροι πρώτοι που ικανοποιούν την (*). Το 2 είναι τετραγωνικό κατάλοιπο όταν

και το 3 είναι όταν

. Το -1 δεν είναι όταν

. Άρα αρκεί να βρούμε άπειρους πρώτους ώστε

και

, που συμβαίνει ας πούμε όταν

. Υπάρχουν άπειροι πρώτοι της μορφής

από το Θεώρημα Dirichlet και τελειώσαμε.
Δημήτρη έχεις άλλη απόδειξη κατά νου;
 για τον οποίο δεν υπάρχει φυσικός αριθμός
για τον οποίο δεν υπάρχει φυσικός αριθμός  ώστε να ισχύει
ώστε να ισχύει  .
.
 για τον οποίο δεν υπάρχει φυσικός αριθμός
για τον οποίο δεν υπάρχει φυσικός αριθμός  ώστε να ισχύει
ώστε να ισχύει  .
.  .
. .
.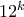 , για
, για  είναι
είναι  , και,
, και,  , αντίστοιχα.
, αντίστοιχα. , για
, για  , και,
, και,  δε διαιρούνται με το 19 για κανένα
δε διαιρούνται με το 19 για κανένα  και
και  για κάθε
για κάθε  δε διαιρούνται με το 19 για κανένα
δε διαιρούνται με το 19 για κανένα  ,
,

 ,
,
 δε διαιρούνται με το 19 για κανένα
δε διαιρούνται με το 19 για κανένα  , για
, για  είναι
είναι  , και,
, και,  , για
, για  , και,
, και,  είναι ένας πρώτος για τον οποίο ο
είναι ένας πρώτος για τον οποίο ο  κάθε φορά για τα οποία δεν ισχύει το συμπέρασμα). Ίσως το τελευταίο να ήταν ένα από τους λόγους για τους οποίους δεν επιλέχθηκε η συγκεκριμένη άσκηση για το διαγωνισμό.
κάθε φορά για τα οποία δεν ισχύει το συμπέρασμα). Ίσως το τελευταίο να ήταν ένα από τους λόγους για τους οποίους δεν επιλέχθηκε η συγκεκριμένη άσκηση για το διαγωνισμό.
 άρα είναι αδύνατη.
άρα είναι αδύνατη. η
η 







 . Αφού τα 2 και 3 είναι τετραγωνικά κατάλοιπα, γράφουμε
. Αφού τα 2 και 3 είναι τετραγωνικά κατάλοιπα, γράφουμε  αλλά αν
αλλά αν  είναι τέτοιος ώστε
είναι τέτοιος ώστε  έχουμε ότι
έχουμε ότι  το οποίο είναι άτοπο γιατί το -1 δεν είναι τετραγωνικό κατάλοιπο.
το οποίο είναι άτοπο γιατί το -1 δεν είναι τετραγωνικό κατάλοιπο. και το 3 είναι όταν
και το 3 είναι όταν  . Το -1 δεν είναι όταν
. Το -1 δεν είναι όταν  . Άρα αρκεί να βρούμε άπειρους πρώτους ώστε
. Άρα αρκεί να βρούμε άπειρους πρώτους ώστε  και
και  , που συμβαίνει ας πούμε όταν
, που συμβαίνει ας πούμε όταν  . Υπάρχουν άπειροι πρώτοι της μορφής
. Υπάρχουν άπειροι πρώτοι της μορφής  να είναι και τα δύο τετραγωνικά υπόλοιπα
να είναι και τα δύο τετραγωνικά υπόλοιπα  . Κατέληξα λίγο διαφορετικά σε αυτό:
. Κατέληξα λίγο διαφορετικά σε αυτό:  άρτιο πρέπει
άρτιο πρέπει  οπότε αν το
οπότε αν το  δεν είναι τετραγωνικό υπόλοιπο
δεν είναι τετραγωνικό υπόλοιπο  περιττό πρέπει
περιττό πρέπει  οπότε αν το
οπότε αν το  δεν είναι τετραγωνικό υπόλοιπο
δεν είναι τετραγωνικό υπόλοιπο  . Από το (β), και χρησιμοποιώντας το
. Από το (β), και χρησιμοποιώντας το 
 είναι
είναι  οπότε θέλω
οπότε θέλω  , δηλαδή
, δηλαδή  . Αυτό δίνει
. Αυτό δίνει  .
. είναι
είναι  οπότε θέλω
οπότε θέλω  , δηλαδή
, δηλαδή  . Αυτό δίνει
. Αυτό δίνει  .
.