
Να αποδειχθεί ότι είναι κυκλική έλικα και να βρεθεί ο άξονάς της.
Συντονιστής: matha


Βαγγέλη,


 .
.Επειδή ένας κύλινδρος ενδέχεται να μην είναι κυκλικός κύλινδρος, είναι προτιμότερο να μιλάμε για κυκλική έλικα, παρά για κυλινδρική.
Αρκεί να δειχθεί ότι είναι γεωμετρικώς ισότιμη με μια της μορφής



 βγαίνει
βγαίνει 
 έχουμε
έχουμε 
 έχουμε
έχουμε 
Βαγγέλη,

Γρηγόρη καλημέρα...


 προέκυψε η εξίσωση της νέας θέσης
προέκυψε η εξίσωση της νέας θέσης
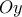


 και φυσικά αν ακολουθήσουμε τις δύο
και φυσικά αν ακολουθήσουμε τις δύο 

 -άρα
-άρα  - προκύπτει ότι η καμπύλη
- προκύπτει ότι η καμπύλη 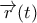 είναι κυκλική έλικα της οποίας το εφαπτόμενο διάνυσμα
είναι κυκλική έλικα της οποίας το εφαπτόμενο διάνυσμα  , για κάθε
, για κάθε  , σχηματίζει σταθερή γωνία
, σχηματίζει σταθερή γωνία  με σταθερό μη-μηδενικό διάνυσμα
με σταθερό μη-μηδενικό διάνυσμα  , δηλαδή ισχύει
, δηλαδή ισχύει 
 για
για  προκύπτουν
προκύπτουν
 προκύπτει το
προκύπτει το  , ενώ ένα παράλληλό του είναι το
, ενώ ένα παράλληλό του είναι το  . Επειδή
. Επειδή 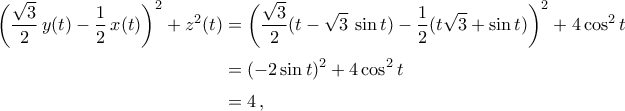
 με εξίσωση
με εξίσωση  . Επειδή η τομή του κυλίνδρου
. Επειδή η τομή του κυλίνδρου  με το επίπεδο
με το επίπεδο  είναι η έλλειψη
είναι η έλλειψη  , της οποίας το κέντρο είναι το
, της οποίας το κέντρο είναι το  , έπεται ότι ο άξονας του κυλίνδρου -άρα και της έλικας- διέρχεται από την αρχή των αξόνων. Συνεπώς η εξίσωση του ζητούμενου άξονα είναι
, έπεται ότι ο άξονας του κυλίνδρου -άρα και της έλικας- διέρχεται από την αρχή των αξόνων. Συνεπώς η εξίσωση του ζητούμενου άξονα είναι 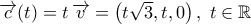 .
.


Σταύρο,ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τρί Ιούλ 26, 2022 9:37 amΠαίρνουμε τον
που είναι πίνακας ορθογωνίου μετασχηματισμού.
Αν τον εφαρμόσουμε στην καμπύλη αυτή γίνεται
που είναι της μορφής που θέλουμε.

Γρηγόρη καλησπέρα...grigkost έγραψε: ↑Τρί Ιούλ 26, 2022 8:51 amΜια 2η λύση:
..................................................
έπεται ότι η έλικα βρίσκεται επί του κυλίνδρουμε εξίσωση
. Επειδή η τομή του κυλίνδρου
με το επίπεδο
είναι η έλλειψη
, της οποίας το κέντρο είναι το
, έπεται ότι ο άξονας του κυλίνδρου -άρα και της έλικας- διέρχεται από την αρχή των αξόνων. Συνεπώς η εξίσωση του ζητούμενου άξονα είναι
.


Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες