KDORTSI έγραψε: ↑Δευ Δεκ 30, 2024 2:29 pm
Δίνεται ένα ορθογώνιο τρίγωνο

με σταθερή την κορυφή

και
μεταβλητές τις άλλες κορυφές

και με

.
Ακόμα είναι:

.
Να βρεθεί η παραμετρική εξίσωση του γεωμετρικού τόπου του μέσου

της
υποτείνουσας

καθώς επίσης και το μήκος της γραμμής αυτής του γ. τόπου.
Αφορμή:
"Περάστε από το  '' στην ακόλουθη διεύθυνση:
https://www.mathematica.gr/forum/viewto ... 22&t=76920
'' στην ακόλουθη διεύθυνση:
https://www.mathematica.gr/forum/viewto ... 22&t=76920
Κώστας Δόρτσιος
S.E.Louridas έγραψε: ↑Δευ Δεκ 30, 2024 7:07 pm
KDORTSI έγραψε: ↑Δευ Δεκ 30, 2024 2:29 pm
Δίνεται ένα ορθογώνιο τρίγωνο

με σταθερή την κορυφή

και
μεταβλητές τις άλλες κορυφές

και με

.
Ακόμα είναι:

. Να βρεθεί η παραμετρική εξίσωση του γεωμετρικού τόπου του μέσου

της
υποτείνουσας

καθώς επίσης και το μήκος της γραμμής αυτής του γ. τόπου.
Κώστας Δόρτσιος
Καλησπέρα Κώστα με τις πλέον ειλικρινείς κορυφαίες ευχές μου για εσένα και τους ανθρώπους σου.
Καταρχάς έχουμε: Έστω

(με

σημείο του άξονα

) παράλληλη στην

Έστω επίσης

σημείο του

τέτοιο ώστε η

να είναι παράλληλη στον άξονα

Έτσι δημιουργούμε το ορθογώνιο

που έχει το ίδιο εμβαδόν με το παραλληλόγραμμο

(κοινό μέρος συμπληρωμένο με ίσα ορθογώνια
τρίγωνα) που είναι

Άρα το σημείο

κινείται σε σταθερό κύκλο κέντρου

διαμέτρου

και βέβαια ακτίνας

Αν τώρα

τότε

με

οπότε μετά από κάποιες πράξεις, καταλήγουμε στην επίλυση του συστήματος
Σ: { }
}
(εύρεση των

με αναμονή τουλάχιστον μία από αυτές να είναι έκφραση του

), ή αν θεωρήσουμε

να επιλύσουμε ως προς

το σύστημα:

Τελικά παίρνουμε:


Άρα έχουμε:

ή

Ο υπολογισμός τώρα του μήκους
της καμπύλης μας, γίνεται με βάση τον τύπο
![L = \int\limits_{{t_1}}^{{t_2}} {\sqrt {{{\left[ {x'\left( t \right)} \right]}^2} + {{\left[ {y'\left( t \right)} \right]}^2}} } dt L = \int\limits_{{t_1}}^{{t_2}} {\sqrt {{{\left[ {x'\left( t \right)} \right]}^2} + {{\left[ {y'\left( t \right)} \right]}^2}} } dt](/forum/ext/geomar/texintegr/latexrender/pictures/7745386271eb6410c29efd01b8584054.png)
, με

Σωτήρη καλημέρα ...
Πολύ ωραία η αντιμετώπιση του θέματος και οι παραμετρικές εξισώσεις σου δουλεύουν μια χαρά και είναι
ίδιες με εκείνες που κι εγώ από άλλη οδό βρήκα.
Ας δούμε πρώτα το σχήμα του τόπου αυτού:

- Γεωμετρικός τόπος κλπ 1.png (18.03 KiB) Προβλήθηκε 1855 φορές
Όπως φαίνεται από το σχήμα αυτό ο τόπος είναι γενικά μια επίπεδη καμπύλη και μάλιστα με ένα
διπλό σημείο.
Θα ήθελα να αναφέρω και τη δικιά μου τακτική:
Πρώτα βρήκα το αντίστροφο

του σημείου

ως πρός κέντρο το σημείο

και
δύναμη ίση με

. Στη συνέχεια το περιέστρεψα κατά μια όρθή γωνία και με θετική φορά
κι έτσι βρήκα τις συντεταγμένες του σημείου

. Αυτές οι δυο ενέργειες μπορούν και γίνονται
εύκολα στο λογισμικό, όμως επειδή έπρεπε να βρούμε όχι το σημείο

αλλά τις συντεταγμένες
αυτού
το θέμα είναι αρκετά ενδιαφέρον. Η εύρεση των συντεταγμένων έγινε "χειροποίητα".
Στις περιπτώσεις αυτές βέβαια έχουμε και άλλα πλεονεκτήματα. Για παράδειγμα αν είχαμε αντί
ορθογωνίου τριγώνου ένα άλλο με γνωστές γωνίες οι τύποι μας λειτουργούν άψογα και δίνουν
άλλη μορφή στο γεωμετρικό τόπο.
Τέλος μήκος της καμπύλης βρίσκεται όπως αναφέρεις με το ολοκλήρωμα που έγραψες. Όμως
τι θα έλεγες ανα θέλαμε το μήκος του βρόγχου που σχηματίζεται;
Υ.Γ. Παραθέτω και τη διεύθυνση του δυναμικού σχήματος:
https://www.geogebra.org/m/ysycwphs
Κώστας Δόρτσιος
 με σταθερή την κορυφή
με σταθερή την κορυφή  και
και  και με
και με  .
. .
. της
της  καθώς επίσης και το μήκος της γραμμής αυτής του γ. τόπου.
καθώς επίσης και το μήκος της γραμμής αυτής του γ. τόπου.  '' στην ακόλουθη διεύθυνση:
'' στην ακόλουθη διεύθυνση: (με
(με  σημείο του άξονα
σημείο του άξονα  ) παράλληλη στην
) παράλληλη στην  Έστω επίσης
Έστω επίσης  σημείο του
σημείο του  τέτοιο ώστε η
τέτοιο ώστε η 

 που έχει το ίδιο εμβαδόν με το παραλληλόγραμμο
που έχει το ίδιο εμβαδόν με το παραλληλόγραμμο  (κοινό μέρος συμπληρωμένο με ίσα ορθογώνια
(κοινό μέρος συμπληρωμένο με ίσα ορθογώνια  Άρα το σημείο
Άρα το σημείο  κινείται σε σταθερό κύκλο κέντρου
κινείται σε σταθερό κύκλο κέντρου  διαμέτρου
διαμέτρου  και βέβαια ακτίνας
και βέβαια ακτίνας 
 τότε
τότε  με
με 
 }
}  με αναμονή τουλάχιστον μία από αυτές να είναι έκφραση του
με αναμονή τουλάχιστον μία από αυτές να είναι έκφραση του  ), ή αν θεωρήσουμε
), ή αν θεωρήσουμε 
 το σύστημα:
το σύστημα: 


 ή
ή  Ο υπολογισμός τώρα του μήκους
Ο υπολογισμός τώρα του μήκους ![L = \int\limits_{{t_1}}^{{t_2}} {\sqrt {{{\left[ {x'\left( t \right)} \right]}^2} + {{\left[ {y'\left( t \right)} \right]}^2}} } dt L = \int\limits_{{t_1}}^{{t_2}} {\sqrt {{{\left[ {x'\left( t \right)} \right]}^2} + {{\left[ {y'\left( t \right)} \right]}^2}} } dt](/forum/ext/geomar/texintegr/latexrender/pictures/7745386271eb6410c29efd01b8584054.png) , με
, με 
 του σημείου
του σημείου  ως πρός κέντρο το σημείο
ως πρός κέντρο το σημείο  και
και  . Στη συνέχεια το περιέστρεψα κατά μια όρθή γωνία και με θετική φορά
. Στη συνέχεια το περιέστρεψα κατά μια όρθή γωνία και με θετική φορά  που υπάρχει παραπάνω, αντιγράφω
που υπάρχει παραπάνω, αντιγράφω 
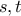 της παραμέτρου με
της παραμέτρου με  .
.  ισοδύναμα
ισοδύναμα  . Άρα
. Άρα  , από όπου
, από όπου 
 , ισοδύναμα
, ισοδύναμα  , από όπου
, από όπου 
 .
.  έως
έως  .
. , βασικό στοιχείο για τη μελέτη του βρόγχου
, βασικό στοιχείο για τη μελέτη του βρόγχου