Συνεχής απεικόνιση

#1

Αποδείξτε ή διαψεύστε:

Υπάρχει $\displaystyle{1-1}$ και συνεχής απεικόνιση του $\displaystyle{\Bbb{R}^2}$ στον $\displaystyle{\Bbb{R}}$

Tolaso J Kos · #2

s.kap έγραψε:Αποδείξτε ή διαψεύστε:

Υπάρχει $\displaystyle{1-1}$ και συνεχής απεικόνιση του $\displaystyle{\Bbb{R}^2}$ στον $\displaystyle{\Bbb{R}}$

Σπύρο,

αυτή είναι γνωστή ασκησούλα και η απάντηση είναι όχι. Δίνω την απάντηση που χω δω δει για αυτό.

Ορίζουμε $\mathcal{A}_x = f(\{x\}\times\mathbb R)$ για κάθε $x \in \mathbb{R}$ . Εφόσον το $\{x\}\times\mathbb R$ είναι συνεκτικό και η

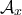είναι συνεχής , τότε πρέπει και το $\mathcal{A}_x$ να 'ναι συνεκτικό. Οπότε είναι διάστημα και μάλιστα μη εκφυλισμένο (non degenerate) αφού η

είναι

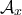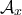. Επομένως καθένα από τα $\mathcal{A}_x$ περιέχει ένα ανοιχτό διάστημα $(\mathfrak{p}_x, \mathfrak{q}_x)$ όπου τα $\mathfrak{p}_x, \; \mathfrak{q}_x$ είναι διακεκριμένοι ρητοί αριθμοί. Εφόσον υπάρχoυν αριθμήσιμα (countable) τέτοια διαστήματα και μη αριθμήσιμα (uncountable) τέτοια σύνολα $\mathcal{A}_x$ , υπάρχουν x, y

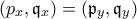με $x \neq y$ τέτοια ώστε $\displaystyle{(\mathfral{p}_x,\mathfrak{q}_x)=(\mathfrak{p}_y,\mathfrak{q}_y)}$ . Αυτό σημαίνει ότι τα διαστήματα $\mathcal{A}_x, \; \mathcal{A}_y$ τέμνονται (intersect) το οποίο οδηγεί σε αντίφαση αφού η

είναι

.

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ · #3

Πιο απλά.
Λόγω συνεκτικότητας το $f(\mathbb{R}^{2})=I$ είναι διάστημα.

Παίρνουμε $a\epsilon I$ εσωτερικό του σημείο.

Το $f(\mathbb{R}^{2}-f^{-1}(a))$ είναι συνεκτικό και ισούται με $I-\left \{ a \right \}$

που δεν είναι συνεκτικό.ΑΤΟΠΟ.

Θα μπορούσαμε να δώσουμε απόδειξη χωρίς να χρησιμοποιήσουμε συνεκτικότητα.Το Θ.Ε.Τ φτάνει

Συνεχής απεικόνιση

Συνεχής απεικόνιση

Re: Συνεχής απεικόνιση

Re: Συνεχής απεικόνιση

Μέλη σε σύνδεση