 .
.Αν
 , συνεχής με
, συνεχής με  , για κάθε
, για κάθε  , να αποδειχθεί ότι η
, να αποδειχθεί ότι η  είναι επί.
είναι επί.Συντονιστής: matha
 .
. , συνεχής με
, συνεχής με  , για κάθε
, για κάθε  , να αποδειχθεί ότι η
, να αποδειχθεί ότι η  είναι επί.
είναι επί. είναι συνεχής συνάρτηση, τότε υπάρχει
είναι συνεχής συνάρτηση, τότε υπάρχει  τέτοιο, ώστε
τέτοιο, ώστε 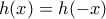 .
. 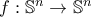 είναι μια συνεχής συνάρτηση με
είναι μια συνεχής συνάρτηση με  για κάθε
για κάθε  και ότι υπάρχει σημείο
και ότι υπάρχει σημείο  . Θεωρούμε τη στερεογραφική προβολή
. Θεωρούμε τη στερεογραφική προβολή  , η οποία είναι συνεχής, 1-1 και επί. Τότε, η
, η οποία είναι συνεχής, 1-1 και επί. Τότε, η  είναι καλά ορισμένη και συνεχής. Από το Θεώρημα Borsuk-Ulam, θα υπάρχει
είναι καλά ορισμένη και συνεχής. Από το Θεώρημα Borsuk-Ulam, θα υπάρχει  τέτοιο, ώστε
τέτοιο, ώστε  Αυτό, όμως, είναι άτοπο, οπότε το συμπέρασμα έπεται.
Αυτό, όμως, είναι άτοπο, οπότε το συμπέρασμα έπεται.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες