 και
και  εφάπτονται εξωτερικά στο σημείο
εφάπτονται εξωτερικά στο σημείο  . Από το
. Από το  , φέρω τη μία
, φέρω τη μία εφαπτομένη
 προς τον
προς τον  , η οποία προεκτεινόμενη τέμνει τον
, η οποία προεκτεινόμενη τέμνει τον  στο
στο  , από το
, από το οποίο φέρω την άλλη εφαπτόμενη προς τον
 , την
, την  . Δείξτε ότι
. Δείξτε ότι 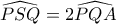
Συντονιστές: cretanman, Demetres, polysot, socrates, silouan
 και
και  εφάπτονται εξωτερικά στο σημείο
εφάπτονται εξωτερικά στο σημείο  . Από το
. Από το  , φέρω τη μία
, φέρω τη μία  προς τον
προς τον  , η οποία προεκτεινόμενη τέμνει τον
, η οποία προεκτεινόμενη τέμνει τον  στο
στο  , από το
, από το  , την
, την  . Δείξτε ότι
. Δείξτε ότι 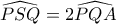
KARKAR έγραψε:Οι κύκλοικαι
εφάπτονται εξωτερικά στο σημείο
. Από το
, φέρω τη μία εφαπτομένη
προς τον
, η οποία προεκτεινόμενη τέμνει τον
στο
, από το οποίο φέρω την άλλη εφαπτόμενη προς τον
, την
. Δείξτε ότι
 Ισχύει
Ισχύει 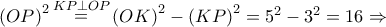
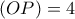
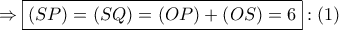
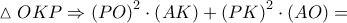
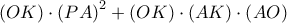
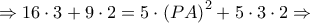
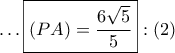 .
. Από το Θεώρημα του Πτολεμαίου στον εγγεγραμμένο "χαρταετό"
Από το Θεώρημα του Πτολεμαίου στον εγγεγραμμένο "χαρταετό" 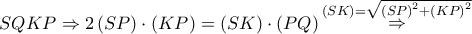
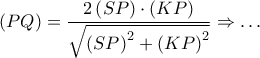
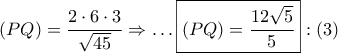 .
.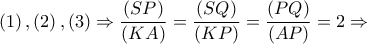
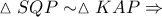

Θανάση και Στάθη Χριστός Ανέστη και εις έτη πολλά .KARKAR έγραψε:Οι κύκλοικαι
εφάπτονται εξωτερικά στο σημείο
. Από το
, φέρω τη μία
εφαπτομένηπρος τον
, η οποία προεκτεινόμενη τέμνει τον
στο
, από το
οποίο φέρω την άλλη εφαπτόμενη προς τον, την
. Δείξτε ότι
 το σημείο τομής των ευθειών
το σημείο τομής των ευθειών 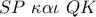 . Ακόμα έστω
. Ακόμα έστω 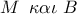 τα αντιδιαμετρικά των
τα αντιδιαμετρικά των 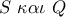 αντίστοιχα.
αντίστοιχα.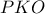 είναι ορθογώνιο στο
είναι ορθογώνιο στο  κι έχει υποτείνουσα
κι έχει υποτείνουσα 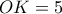 και κάθετη πλευρά
και κάθετη πλευρά 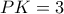 θα είναι
θα είναι 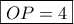 .
. 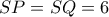 κι επειδή το τετράπλευρο
κι επειδή το τετράπλευρο 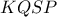 έχει τις γωνίες στα
έχει τις γωνίες στα  ορθές θα είναι εγγράψιμο και τα ορθογώνια τρίγωνα
ορθές θα είναι εγγράψιμο και τα ορθογώνια τρίγωνα 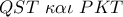 όμοια.
όμοια.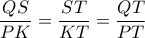 και αφού
και αφού 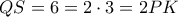 θα είναι
θα είναι 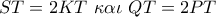 .
.  στο μεγάλο κύκλο έχουμε
στο μεγάλο κύκλο έχουμε 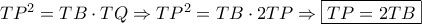 .
. 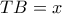 από το Π. Θ. στο τρίγωνο
από το Π. Θ. στο τρίγωνο 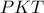 θα προκύψει:
θα προκύψει: 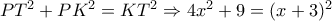 απ’ όπου
απ’ όπου 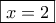 .
.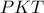 θα έχει πλευρές :
θα έχει πλευρές : 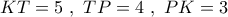 και άρα ίσο με το
και άρα ίσο με το 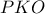 .
.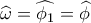 και αφού
και αφού 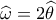 ( επίκεντρη με αντίστοιχη εγγεγραμμένη ) θα είναι και
( επίκεντρη με αντίστοιχη εγγεγραμμένη ) θα είναι και 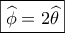 .
.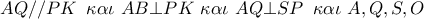 ανήκουν στο ίδιο κύκλο .
ανήκουν στο ίδιο κύκλο . ..και μια λύση με χρήση εμβαδών...KARKAR έγραψε:Οι κύκλοικαι
εφάπτονται εξωτερικά στο σημείο
. Από το
, φέρω τη μία
εφαπτομένηπρος τον
, η οποία προεκτεινόμενη τέμνει τον
στο
, από το
οποίο φέρω την άλλη εφαπτόμενη προς τον, την
. Δείξτε ότι
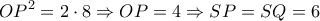
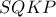 εγγράψιμο
εγγράψιμο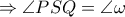 .Άρα τα ισοσκελή τρίγωνα
.Άρα τα ισοσκελή τρίγωνα 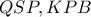 είναι όμοια ,οπότε
είναι όμοια ,οπότε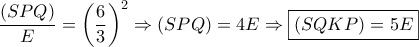
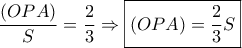 και
και 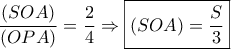 και
και 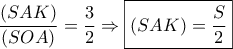
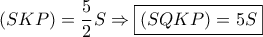
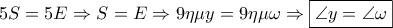
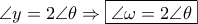
Το τετράπλευρο
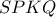 έχει τις γωνίες του στα
έχει τις γωνίες του στα ορθές , άρα είναι εγγράψιμο σε κύκλο διαμέτρου
ορθές , άρα είναι εγγράψιμο σε κύκλο διαμέτρου  .
. η
η  διχοτομεί την γωνία
διχοτομεί την γωνία 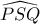 . Προφανές ότι
. Προφανές ότι 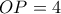 .
.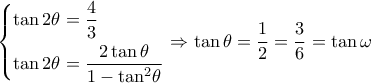 .
Αφού οι γωνίες είναι οξείες θα έχω:
.
Αφού οι γωνίες είναι οξείες θα έχω: 
 . !
. !Με το Π.Θ στο ορθ.
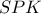 έχουμε
έχουμε 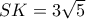
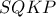 ισχύει
ισχύει 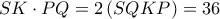
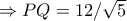 .
.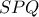 , πλευρών
, πλευρών 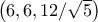 , ο νόμος συνημιτόνων δίνει
, ο νόμος συνημιτόνων δίνει 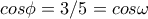
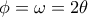 . Φιλικά, Γιώργος
. Φιλικά, ΓιώργοςΜέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες