Σελίδα 1 από 1
Μεσογειάδα 2006
Δημοσιεύτηκε: Κυρ Νοέμ 07, 2010 2:58 pm
από nickthegreek
Το παρακάτω πρόβλημα ήταν το τέταρτο πρόβλημα του Μεσογειακού μαθηματικού διαγωνισμού 2006 και θεωρείται εξαιρετικά δύσκολη ανισότητα.Προσωπικά ούτε μπορώ να καταλάβω την εκφώνηση,και δεν με πειράζει να το παραδεχτώ.Ελπίζω κάποιος να μου εξηγήσει τι σημαίνουν τα διπλά αυτά γινόμενα.Το δίνω στο mathematica διότι έχει μια καταπληκτική λύση,την οποία έχει βρει ένας φίλος μου από τη Δράμα και σπουδαίος δάσκαλος,που αυτή την στιγμή βρίσκεται στο Harvard.Ιδού το πρόβλημα:
Έστω

θετικοί ακέραιοι και έστω:
![x_{i,j}\in [0,1] x_{i,j}\in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/e7fd208e73fce11bbd96fe608f7d4b41.png)
για

και
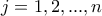
Να αποδείξετε ότι:

Νομίζω πως αυτή η ανισότητα έχει πολλά πράγματα για τα οποία μπορούμε να συζητήσουμε,και για αυτό το λόγο την ανεβάζω.
Περιμένω τις λύσεις σας.
Φιλικά,
Νίκος
Εdit:Διορθώνω την εκφώνηση της άσκησης μετά από την σωστή παρατήρηση του Σιλουανού,τον οποίο και ευχαριστώ
Re: Μεσογειάδα 2006
Δημοσιεύτηκε: Κυρ Νοέμ 07, 2010 3:28 pm
από gtk1994
Μπορείς να κοιτάξεις τη λύση αυτού του προβλήματος στο βιβλίο του κυρίου Φελλούρη " Οι Πανελλήνιοι Μαθηματικοί Διαγωνισμοί 1997-2007 " (σελ.313).
Αν προλάβω θα τη γράψω και εδώ σε περίπτωση που δε διαθέτεις το βιβλίο ( δε σου υπόσχομαι και πολλά ,όμως, γιατί διαβάζω και για ένα διαγώνισμα φυσικής

)
Re: Μεσογειάδα 2006
Δημοσιεύτηκε: Κυρ Νοέμ 07, 2010 3:33 pm
από nickthegreek
Φίλε μου,
Την λύση την έχω.Αν θέλεις ανεβάζεις τη λύση που έχεις.Πληροφοριακά να πούμε ότι στο βιβλίο του κυρίου Φελλούρη η λύση χρησιμοποιεί διπλή επαγωγή.Υπάρχει και άλλη λύση,που είναι πολύ πιο όμορφη.
Περιμένω τις απόψεις σας.
Φιλικά,
Νίκος
Re: Μεσογειάδα 2006
Δημοσιεύτηκε: Κυρ Νοέμ 07, 2010 4:05 pm
από Demetres
Η δυσκολία του προβλήματος βρίσκεται ακριβώς στην κατανόηση. Άμα κατανοηθεί τι ζητάει η λύση είναι ουσιαστικά δυο γραμμές. Γράφω την ζητούμενη ανισότητα για την περίπτωση

. (Φαντάζομαι ότι το δεδομένο είναι πως

)

Re: Μεσογειάδα 2006
Δημοσιεύτηκε: Κυρ Νοέμ 07, 2010 4:14 pm
από billy_scabilly
Yποθέτοντας ότι εννοείς ότι τα xi,j ανήκουν στο {0,1} δίνω μια πιθανή λύση(μην φωνάζετε αν έχω κάνει λάθος)

:
Kατασκευάζουμε τον πίνακα Α με εγγραφές τo xi,j στην i,j εγγραφή.Βλέπουμε ότι κάθε ένα από τα δύο γινόμενα στο αριστερό μέλος μπορεί να είναι ή 0 ή 1. Έστω ότι και τα δύο είναι μηδέν.Τότε από το πρώτο γινόμενο έχουμε μια στήλη όλη 1 και από το δεύτερο γινόμενο μια γραμμή όλη 0.Αυτό είναι άτοπο όμως γιατί κάθε γραμμή και στήλη έχουν ένα κοινό στοιχείο.

Re: Μεσογειάδα 2006
Δημοσιεύτηκε: Κυρ Νοέμ 07, 2010 4:40 pm
από nickthegreek
Άσχετο:
Ο μεσογειακός μαθηματικός διαγωνισμός σταμάτησε να γίνεται;;;Γιατί δεν μπορώ να βρω θέματα μετά το 2007...
Φιλικά,
Νίκος
Re: Μεσογειάδα 2006
Δημοσιεύτηκε: Κυρ Νοέμ 07, 2010 4:45 pm
από kwstas12345
Kαλησπέρα και από μένα!
Νίκο, όχι δεν έχει σταματησει ,τα θέματα δημοσιεύονται στο περιοδικό του ευκλείδη Β ....νομίζω πως τα θέματα μπορείς ενδεχομένως να τα βρείς και από την επίσημη σελίδα της μαθηματικής εταιρείας της Ισπανίας που είναι και διοργανώτρια από όσο ξέρω...
Φιλικά,
Κώστας
Re: Μεσογειάδα 2006
Δημοσιεύτηκε: Κυρ Νοέμ 07, 2010 4:49 pm
από nickthegreek
Σ'ευχαριστώ Κώστα!!!Παρόλ'αυτά όμως, οι Έλληνες δίνουν πια προκριματικό διαγωνισμό σε επίπεδο εθνικό και δεν συμμετέχουν στον Μεσογειακό Διαγωνισμό.Μήπως κάνω λάθος;;;
Φιλικά,
Νίκος
Υ.Γ.(Σόρι που ρωτάω πράγματα άσχετα με την άσκηση)
Re: Μεσογειάδα 2006
Δημοσιεύτηκε: Κυρ Νοέμ 07, 2010 4:59 pm
από Dimitris X
nickthegreek έγραψε:Σ'ευχαριστώ Κώστα!!!Παρόλ'αυτά όμως, οι Έλληνες δίνουν πια προκριματικό διαγωνισμό σε επίπεδο εθνικό και δεν συμμετέχουν στον Μεσογειακό Διαγωνισμό.Μήπως κάνω λάθος;;;
Φιλικά,
Νίκος
Υ.Γ.(Σόρι που ρωτάω πράγματα άσχετα με την άσκηση)
Η συμμετοχή είναι προαιρετική...Κάτι σαν test ικανοτήτων....

Re: Μεσογειάδα 2006
Δημοσιεύτηκε: Κυρ Νοέμ 07, 2010 5:24 pm
από nickthegreek
Αφήνω το θέμα ανοιχτό κι αν δε βρεθεί η ίδια λύση με αυτήν που έχω υπ'όψην μου,θα την ανεβάσω σε μια-δυο μέρες.
Φιλικά
Re: Μεσογειάδα 2006
Δημοσιεύτηκε: Κυρ Νοέμ 07, 2010 5:52 pm
από silouan
Η εκφώνηση έλεγε ότι
![x_{ij}\in [0,1] x_{ij}\in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/e650cf60ff07903cad9a2d72716dbba5.png)
. Τελικά όμως αναγόμαστε στην περίπτωση που γράφτηκε αρχικά το πρόβλημα. Τυχαίο ;

Re: Μεσογειάδα 2006
Δημοσιεύτηκε: Κυρ Νοέμ 07, 2010 7:31 pm
από achilleas
nickthegreek έγραψε:....
Έστω

θετικοί ακέραιοι και έστω:
![x_{i,j}\in [0,1] x_{i,j}\in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/e7fd208e73fce11bbd96fe608f7d4b41.png)
για

και
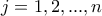
Να αποδείξετε ότι:

...
Το πρόβλημα αυτό το βρίσκουμε κι ως πρόβλημα 4.3 στο βιβλίο των P.Biler, Alfred Witkowski, Problems in Mathematical Analysis
Δεν αναφέρει την πηγή του, αλλά έχει την εξής υπόδειξη στη σελίδα 154:
Υπόδειξη: Παρατηρήστε ότι

. Δώστε μια πιθανοθεωρητική εξήγηση της ζητούμενης ανισότητας.
Φιλικά,
Αχιλλέας
Re: Μεσογειάδα 2006
Δημοσιεύτηκε: Κυρ Νοέμ 07, 2010 11:31 pm
από Demetres
Θα δώσω μια απάντηση διαφορετική από αυτή που προτείνει ο Αχιλλέας. Πάλι χρησιμοποιεί πιθανότητες (στα κρυφά) αλλά μέσω ενός αρκετά ισχυρού λήμματος που μας απαλλάσσει από το να ψάχνουμε κάθε φορά ποιο σύνολο περιέχεται σε ποιο άλλο σύνολο.
Κατ' αρχήν παρατηρούμε ότι η ανισότητα ισχύει αν

για κάθε

. (Έχει ήδη εξηγήσει γιατί ο billy_scabilly)
Αρκεί να αποδείξουμε το ακόλουθο λήμμα
Λήμμα: Έστω

ένα πολυώνυμο το οποίο είναι γραμμικό σε κάθε ένα από τα

. Αν

για κάθε
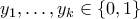
τότε

για κάθε
![y_1,\ldots,y_k \in [0,1] y_1,\ldots,y_k \in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/93e5a55bdbfb6bc2255ebb738aef6e68.png)
Για την απόδειξη του λήμματος ισχυρίζομαι ότι

για κάποια

. Για την απόδειξη του ισχυρισμού αρκεί να δείξω ότι κάθε όρος του πολυωνύμου μπορεί να γραφτεί σε αυτήν την μορφή. Χωρίς βλάβη της γενικότητας αρκεί να δείξω ότι ο όρος

μπορεί να γραφεί σε αυτήν την μορφή. Όμως

Η τελευταία ισότητα μπορεί να αποδειχθεί με επαγωγή στο

αν και ο πιο εύκολος τρόπος για να δει κάποιος ότι ισχύει είναι με χρήση πιθανοτήτων. (Πώς;)
Έχοντας τώρα στην διάθεσή μας αυτό το λήμμα, η απόδειξη είναι πλέον απλή. Για κάθε

παίρνουμε

. Τότε

. Άρα

για κάθε

και άρα

για κάθε
![y_1,\ldots,y_k \in [0,1] y_1,\ldots,y_k \in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/93e5a55bdbfb6bc2255ebb738aef6e68.png)
.
Re: Μεσογειάδα 2006
Δημοσιεύτηκε: Δευ Νοέμ 08, 2010 9:57 am
από nickthegreek
Ευχαριστώ πολύ τον Δημήτρη για τη λύση του!!!Από αυτήν θα ήθελα να κρατήσω το σημαντικό γεγονός-λήμμα ότι αν μια συνάρτηση είναι γραμμική ως προς κάθε της μεταβλητή τότε παίρνει τα ακρότατά της στα άκρα των διαστημάτων που ορίζεται.
Έτσι λοιπόν με βάση αυτό το λήμμα θα έχουμε ότι όλα τα

είναι ίσα με 0 ή 1, όταν έχουμε ελάχιστο.
Παρόμοια λύση με αυτή του Δημήτρη (αυτή που είχα εγώ υπ'όψιν μου) δόθηκε από τον Στέργιο Αντωνακούδη.
Φιλικά,
Νίκος
Re: Μεσογειάδα 2006
Δημοσιεύτηκε: Δευ Νοέμ 08, 2010 11:44 am
από Demetres
nickthegreek έγραψε:
Παρόμοια λύση με αυτή του Δημήτρη (αυτή που είχα εγώ υπ'όψιν μου) δόθηκε από τον Στέργιο Αντωνακούδη.
Δράμα, Harvard, έπρεπε να το υποψιαστώ. Νίκο, να του στείλεις πολλά χαιρετίσματα.
Re: Μεσογειάδα 2006
Δημοσιεύτηκε: Πέμ Νοέμ 11, 2010 3:36 pm
από nickthegreek
Μπορεί κάποιος να ανεβάσει τη λύση με τις πιθανότητες;;;
Ευχαριστώ εκ των προτέρων.
Re: Μεσογειάδα 2006
Δημοσιεύτηκε: Πέμ Νοέμ 11, 2010 4:43 pm
από Demetres
nickthegreek έγραψε:Μπορεί κάποιος να ανεβάσει τη λύση με τις πιθανότητες;;;
Ευχαριστώ εκ των προτέρων.
Έστω

ανεξάρτητα ενδεχόμενα με

.
Ας αποδείξουμε πρώτα την υπόδειξη του Αχιλλέα

Αν

τότε θα υπάρχει

ώστε

για κάθε
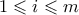
. Αλλά τότε

για κάθε

και άρα

Άρα θα έχουμε
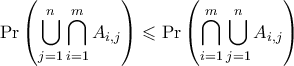
Αλλά

και

Το ζητούμενο έπεται.
 θετικοί ακέραιοι και έστω:
θετικοί ακέραιοι και έστω:![x_{i,j}\in [0,1] x_{i,j}\in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/e7fd208e73fce11bbd96fe608f7d4b41.png) για
για  και
και 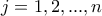

 θετικοί ακέραιοι και έστω:
θετικοί ακέραιοι και έστω:![x_{i,j}\in [0,1] x_{i,j}\in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/e7fd208e73fce11bbd96fe608f7d4b41.png) για
για  και
και 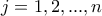

 . (Φαντάζομαι ότι το δεδομένο είναι πως
. (Φαντάζομαι ότι το δεδομένο είναι πως  )
)
![x_{ij}\in [0,1] x_{ij}\in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/e650cf60ff07903cad9a2d72716dbba5.png) . Τελικά όμως αναγόμαστε στην περίπτωση που γράφτηκε αρχικά το πρόβλημα. Τυχαίο ;
. Τελικά όμως αναγόμαστε στην περίπτωση που γράφτηκε αρχικά το πρόβλημα. Τυχαίο ;  . Δώστε μια πιθανοθεωρητική εξήγηση της ζητούμενης ανισότητας.
. Δώστε μια πιθανοθεωρητική εξήγηση της ζητούμενης ανισότητας. . (Έχει ήδη εξηγήσει γιατί ο billy_scabilly)
. (Έχει ήδη εξηγήσει γιατί ο billy_scabilly) ένα πολυώνυμο το οποίο είναι γραμμικό σε κάθε ένα από τα
ένα πολυώνυμο το οποίο είναι γραμμικό σε κάθε ένα από τα  . Αν
. Αν  για κάθε
για κάθε 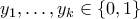 τότε
τότε ![y_1,\ldots,y_k \in [0,1] y_1,\ldots,y_k \in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/93e5a55bdbfb6bc2255ebb738aef6e68.png)

 . Για την απόδειξη του ισχυρισμού αρκεί να δείξω ότι κάθε όρος του πολυωνύμου μπορεί να γραφτεί σε αυτήν την μορφή. Χωρίς βλάβη της γενικότητας αρκεί να δείξω ότι ο όρος
. Για την απόδειξη του ισχυρισμού αρκεί να δείξω ότι κάθε όρος του πολυωνύμου μπορεί να γραφτεί σε αυτήν την μορφή. Χωρίς βλάβη της γενικότητας αρκεί να δείξω ότι ο όρος  μπορεί να γραφεί σε αυτήν την μορφή. Όμως
μπορεί να γραφεί σε αυτήν την μορφή. Όμως 
 αν και ο πιο εύκολος τρόπος για να δει κάποιος ότι ισχύει είναι με χρήση πιθανοτήτων. (Πώς;)
αν και ο πιο εύκολος τρόπος για να δει κάποιος ότι ισχύει είναι με χρήση πιθανοτήτων. (Πώς;) παίρνουμε
παίρνουμε  . Τότε
. Τότε  . Άρα
. Άρα  για κάθε
για κάθε  και άρα
και άρα 
 είναι ίσα με 0 ή 1, όταν έχουμε ελάχιστο.
είναι ίσα με 0 ή 1, όταν έχουμε ελάχιστο. ανεξάρτητα ενδεχόμενα με
ανεξάρτητα ενδεχόμενα με  .
.
 τότε θα υπάρχει
τότε θα υπάρχει  ώστε
ώστε  για κάθε
για κάθε 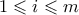 . Αλλά τότε
. Αλλά τότε  για κάθε
για κάθε  και άρα
και άρα