Δίνονται οι θετικοί ακέραιοι a, b, n , b > 1 και το a είναι πολ/σιο του
 . Rewritten a to the base b (μένει ως έχει, καθώς δεν έχω κατα νού ακριβή μετάφραση
. Rewritten a to the base b (μένει ως έχει, καθώς δεν έχω κατα νού ακριβή μετάφραση Πρόβλημα 2
Εστω x, y, z πραγματικοί αριθμοι ωστε
 και
και  . Να βρεθεί η μέγιστη τιμη της παραστασης
. Να βρεθεί η μέγιστη τιμη της παραστασης 
Πρόβλημα 3
Βρείτε ολες τις συναρτήσεις
 ωστε
ωστε 
Πρόβλημα 4
Το K είναι η τομή των διαγωνίων του τετραπλέυρου ABCD όπου
 και AC = AB + AD. να αποδειχθεί οτι οι ακτίνες των εγγεγραμμένων κύκλων στα τρίγωνα ABK και ADK είναι ίσες.
και AC = AB + AD. να αποδειχθεί οτι οι ακτίνες των εγγεγραμμένων κύκλων στα τρίγωνα ABK και ADK είναι ίσες.
 είναι
είναι  , δηλαδή υπάρχει
, δηλαδή υπάρχει  ώστε
ώστε 
 έχουμε
έχουμε  .
. έχουμε
έχουμε  οπότε
οπότε 
 είναι
είναι  , δηλαδή
, δηλαδή 
 και καταλήγουμε σε άτοπο(
και καταλήγουμε σε άτοπο( ).
). προκύπτει ότι το τετράπλευρο είναι εγγράψιμο σε κύκλο διαμέτρου
προκύπτει ότι το τετράπλευρο είναι εγγράψιμο σε κύκλο διαμέτρου  .Με την βοήθεια της εφαπτομένης
.Με την βοήθεια της εφαπτομένης  στο
στο  προκύπτουν οι γωνίες του σχήματος. Συμβολίζουμε:
προκύπτουν οι γωνίες του σχήματος. Συμβολίζουμε:  (για ευκολία).
(για ευκολία). 
 έχουμε
έχουμε  . Όμως
. Όμως  , άρα
, άρα 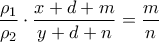 .
.  αρκεί
αρκεί  , δηλαδή αρκεί να αποδείξουμε ότι
, δηλαδή αρκεί να αποδείξουμε ότι  .
. , καθώς και
, καθώς και  .
. .
.



 το οποίο ισχύει και η απόδειξη ολοκληρώθηκε.
το οποίο ισχύει και η απόδειξη ολοκληρώθηκε. γραμμένος σε βάση
γραμμένος σε βάση  .
.  στις θέσεις
στις θέσεις  με
με  . Θέτουμε
. Θέτουμε  στη θέση
στη θέση  και
και  στη θέση
στη θέση  (μεταφέροντας τα τυχόν κρατούμενα). Ο αριθμός μας εξακολουθεί να είναι πολ/σιο του
(μεταφέροντας τα τυχόν κρατούμενα). Ο αριθμός μας εξακολουθεί να είναι πολ/σιο του  , είναι αυστηρά μικρότερος από πριν και έχει ίσο ή μικρότερο πλήθος μη μηδενικών ψηφίων.
, είναι αυστηρά μικρότερος από πριν και έχει ίσο ή μικρότερο πλήθος μη μηδενικών ψηφίων. . Προφανώς αυτός ο αριθμός θα είναι ο
. Προφανώς αυτός ο αριθμός θα είναι ο  μη μηδενικά ψηφία. Αρα ο αρχικός αριθμός μας έχει τουλάχιστον
μη μηδενικά ψηφία. Αρα ο αρχικός αριθμός μας έχει τουλάχιστον  ώστε
ώστε