 τέτοιες ώστε
τέτοιες ώστε  για κάθε
για κάθε 
Συντονιστές: cretanman, Demetres, polysot, achilleas, socrates, silouan
 τέτοιες ώστε
τέτοιες ώστε  για κάθε
για κάθε 
 .Απο την
.Απο την  προκύπτει ότι
προκύπτει ότι







 και
και 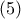 προκύπτει οτι για κάθε
προκύπτει οτι για κάθε  ισχύει
ισχύει  .
. ,όπου
,όπου  το σύνολο των ριζών της εξίσωσης
το σύνολο των ριζών της εξίσωσης  στο
στο  .
. αποδ. ότι για κάθε
αποδ. ότι για κάθε  και για κάθε
και για κάθε  ισχύει
ισχύει  .
. ,τότε είναι φανερό ότι υπάρχει
,τότε είναι φανερό ότι υπάρχει  ώστε
ώστε  ,οπότε ,λόγω της
,οπότε ,λόγω της  ,εχουμε
,εχουμε  .
. .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες