 που ορίζεται αναδρομικά από τις σχέσεις:
που ορίζεται αναδρομικά από τις σχέσεις: 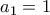 και
και 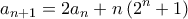
για κάθε θετικό ακέραιο
 .
.Συντονιστές: cretanman, Demetres, polysot, achilleas, socrates, silouan
 που ορίζεται αναδρομικά από τις σχέσεις:
που ορίζεται αναδρομικά από τις σχέσεις: 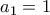 και
και 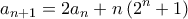
 .
.![{a_{n + 1}} - \left[ {\left( {{{\left( {n + 1} \right)}^2} - \left( {n + 1} \right)} \right){2^{\left( {n + 1} \right) - 2}} - \left( {\left( {n + 1} \right) + 1} \right)} \right] = {a_{n + 1}} - \left[ {\left( {{{\left( {n + 1} \right)}^2} - \left( {n + 1} \right)} \right){2^{\left( {n + 1} \right) - 2}} - \left( {\left( {n + 1} \right) + 1} \right)} \right] =](/forum/ext/geomar/texintegr/latexrender/pictures/a64d86a76e362f42ce5bcad2bf7919e2.png)
![2\left[ {{a_n} - \left( {\left( {{n^2} - n} \right){2^{n - 2}} - \left( {n + 1} \right)} \right)} \right] \Rightarrow {b_{n + 1}} = 2{b_n} 2\left[ {{a_n} - \left( {\left( {{n^2} - n} \right){2^{n - 2}} - \left( {n + 1} \right)} \right)} \right] \Rightarrow {b_{n + 1}} = 2{b_n}](/forum/ext/geomar/texintegr/latexrender/pictures/434dd6d2e50a3e3aadb50fcf6360ab60.png) ,
,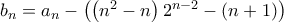 .
.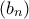 είναι γεωμετρική πρόοδος με λόγο
είναι γεωμετρική πρόοδος με λόγο  έχουμε
έχουμε 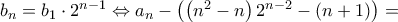
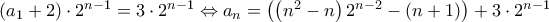

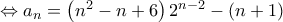 .
. έχει λύση
έχει λύση 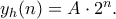
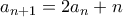 αναζητούμε μερική λύση της μορφής
αναζητούμε μερική λύση της μορφής 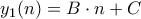
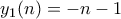 )
)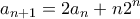 αναζητούμε μερική λύση της μορφής
αναζητούμε μερική λύση της μορφής 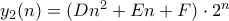
 μπροστά από το
μπροστά από το 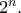
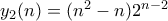 )
)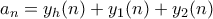
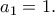 )
)Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 10 επισκέπτες