 τέτοιες ώστε
τέτοιες ώστε  για κάθε
για κάθε 
Συντονιστές: cretanman, Demetres, polysot, achilleas, socrates, silouan
 τέτοιες ώστε
τέτοιες ώστε  για κάθε
για κάθε 
Γιαsocrates έγραψε:Να προσδιορίσετε όλες τις συναρτήσειςτέτοιες ώστε
για κάθε
 , έχουμε
, έχουμε  .
. με
με 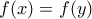 , τότε
, τότε 
 .
. είναι
είναι  .
. έχουμε
έχουμε 
 , όπου
, όπου  .
. είναι
είναι  , άρα
, άρα  .
. , άρα
, άρα  που επαληθεύει.
που επαληθεύει.kostas_zervos έγραψε:Γιαsocrates έγραψε:Να προσδιορίσετε όλες τις συναρτήσειςτέτοιες ώστε
για κάθε
, έχουμε
.
Έστωμε
, τότε
.
Άρα ηείναι
.
Γιαέχουμε
, όπου
.
Αλλά ηείναι
, άρα
.
Αντικαθιστώντας στην αρχική έχουμε
, άρα
που επαληθεύει.
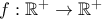 τέτοιες ώστε
τέτοιες ώστε  για κάθε
για κάθε 
Να το δούμε,
 η δοσμένη. Αν
η δοσμένη. Αν  παίρνω
παίρνω  άρα η
άρα η  είναι
είναι 
 με
με  .
.  σταθεροποιώντας το
σταθεροποιώντας το  είναι άμεσο πως η
είναι άμεσο πως η  είναι επί σε διάστημα της μορφής
είναι επί σε διάστημα της μορφής 

 για μεγάλα
για μεγάλα  .
. για κάθε
για κάθε  και
και  μεγάλο, οπότε και
μεγάλο, οπότε και 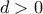
 αρκετά μεγάλο
αρκετά μεγάλο 
 για κάθε
για κάθε  .
. επί σε
επί σε  μπορώ να βρω
μπορώ να βρω  με
με  , κάποιο αρκετά μεγάλο πολλάπλάσιο του
, κάποιο αρκετά μεγάλο πολλάπλάσιο του 


 και αφού η
και αφού η  επί σε
επί σε  έχω
έχω  για μεγάλα
για μεγάλα 
 παίρνω ακεραίους
παίρνω ακεραίους  αρκετά μεγάλους , τότε
αρκετά μεγάλους , τότε 

 επομένως
επομένως  για μεγάλα
για μεγάλα 
 επιλέγω
επιλέγω  μεγάλο ακέραιο οπότε
μεγάλο ακέραιο οπότε 

 η οποία και επαληθεύει.
η οποία και επαληθεύει.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες