ΓΕΩΜΕΤΡIΑ. ΠΡΩΤΟΕΜΦΑΝΙΖΟΜΕΝΕΣ ΠΡΟΤΑΣΕΙΣ.
Συντονιστές: cretanman, Demetres, polysot, socrates, silouan, rek2
-
ΝΙΚΟΣ
- Διακεκριμένο Μέλος
- Δημοσιεύσεις: 1888
- Εγγραφή: Παρ Νοέμ 13, 2009 8:35 pm
- Τοποθεσία: Καλαμαριά (Θεσσαλονίκη).
Re: ΓΕΩΜΕΤΡIΑ. ΠΡΩΤΟΕΜΦΑΝΙΖΟΜΕΝΕΣ ΠΡΟΤΑΣΕΙΣ.
Δε θα απαντήσω στις κατηγορίες και στα υπονοούμενα του κ. Μ. Λάμπρου, αν και έχω υποχρέωση να υπερασπίσω τον εαυτό μου, γιατί και πάλι θα βγω ζημιωμένος, καθώς θα διαγραφούν επιλεκτικά, ως συνήθως και θα μείνουν μόνο οι κατηγορίες για να μου προσβάλουν την τιμή και υπόληψη. Όπως για παράδειγμα συνέβη στον παρακάτω σύνδεσμο και όχι μόνο, όπου διαγράφηκε μόνο η απολογία μου, ενώ παραμένουν οι κατηγορίες. Είναι δίκαιο; Είναι ηθικό;
viewtopic.php?f=22&t=76073&start=120
ποστ 136, 137 και 138.
Εξάλλου, αν ασχοληθώ τώρα με παλιές ιστορίες, θα αποπροσανατολίσω τα πράγματα (Όπως κάνει παραπάνω ο κ. Λάμπρου) και θα ξεφύγουμε από την ουσία που είναι η λύση του δοσμένου προβλήματος και που δε θα το ήθελα. Η απάντησή μου θα πραγματοποιηθεί, όχι όμως τώρα.
Το δοσμένο πρόβλημα στην ουσία είναι η κατασκευή αρμονικού δεκάγωνου (Του οποίου ορισμοί, επεξηγήσεις, πληροφορίες και λεπτομερή σχήματα δίνονται στον παρακάτω σύνδεσμο) και μόνο για το οποίο (αρμονικό δεκάγωνο) αληθεύουν και οι 17 ιδιότητες του δοσμένου προβλήματος.
Το ερώτημά μου είναι:
Έχει κάποια σχέση η παραπάνω δοσμένη λύση και τα σχήματά της, με όλα αυτά που αναφέρονται στο δοσμένο πρόβλημα του παρακάτω συνδέσμου; Η διαπίστωση μπορεί να γίνει μόνο με μιά ματιά.
Θα ήθελα την απάντηση εκείνων που αγαπούν τη Γεωμετρία και που δε θέλουν να την βλέουν να ποδο-πατιέται.
https://drive.google.com/file/d/1MA40GS ... HEp3s/view
Νίκος Δ. Κυριαζή
Εξακολουθεί να ισχύει και η παρακάτω απάντησή μου:
Επί του παρόντος δε θα μπω σε λεπτομέρειες για να αποφανθώ ότι ατυχώς η απόδειξή σου δεν είναι σωστή, καθώς δεν αποδεικνύεις έστω τις δύο από τις κυριότερες ιδιότητες του ζητούμενου δεκαπλεύρου, που είναι οι παράγραφοι (γ) και (ιβ).
Οι ιδιότητες των παραγράφων (α), (β), (δ), που μέχρι τώρα απέδειξες, αληθεύουν σε όλα τα δεκάπλευρα που έχουν συντρέχουσες διαγώνιες (κύριες). Τούτο σημαίνει ότι δεν έχουμε αγγίξει ακόμα τη λύση του προβλήματος.
Για την ιδιότητα της παραγράφου (γ), το πρόβλημα δε ζητά αυτό που απέδειξες μόνο, δηλαδή της πέντε ισότητες μεμονωμένα, αλλά και ότι αυτές πρέπει να είναι και μεταξύ τους ίσες. Γράφεις ότι για να συμβεί αυτό θα πρέπει οι πέντε πρώτες διαδοχικές πλευρές του δεκαπλεύρου να είναι ίσες, αλλά δε το δικαιολογείς.
Ειδικά την ιδιότητα της παραγράφου (ιβ), δεν την απέδειξες, όπως και τις υπόλοιπες παραγράφους από (ε) μέχρι (ιζ), που πρέπει να αποδειχθούν για να έχουμε επιτύχει λύση του προβλήματος και οι οποίες δεν είναι εύκολες όπως λες, αντίθετα αποτελούν τη δυσκολία του προβλήματος, μαζί με εκείνη της παραγράφου (γ).
Νίκος Δ. Κυριαζής
viewtopic.php?f=22&t=76073&start=120
ποστ 136, 137 και 138.
Εξάλλου, αν ασχοληθώ τώρα με παλιές ιστορίες, θα αποπροσανατολίσω τα πράγματα (Όπως κάνει παραπάνω ο κ. Λάμπρου) και θα ξεφύγουμε από την ουσία που είναι η λύση του δοσμένου προβλήματος και που δε θα το ήθελα. Η απάντησή μου θα πραγματοποιηθεί, όχι όμως τώρα.
Το δοσμένο πρόβλημα στην ουσία είναι η κατασκευή αρμονικού δεκάγωνου (Του οποίου ορισμοί, επεξηγήσεις, πληροφορίες και λεπτομερή σχήματα δίνονται στον παρακάτω σύνδεσμο) και μόνο για το οποίο (αρμονικό δεκάγωνο) αληθεύουν και οι 17 ιδιότητες του δοσμένου προβλήματος.
Το ερώτημά μου είναι:
Έχει κάποια σχέση η παραπάνω δοσμένη λύση και τα σχήματά της, με όλα αυτά που αναφέρονται στο δοσμένο πρόβλημα του παρακάτω συνδέσμου; Η διαπίστωση μπορεί να γίνει μόνο με μιά ματιά.
Θα ήθελα την απάντηση εκείνων που αγαπούν τη Γεωμετρία και που δε θέλουν να την βλέουν να ποδο-πατιέται.
https://drive.google.com/file/d/1MA40GS ... HEp3s/view
Νίκος Δ. Κυριαζή
Εξακολουθεί να ισχύει και η παρακάτω απάντησή μου:
Επί του παρόντος δε θα μπω σε λεπτομέρειες για να αποφανθώ ότι ατυχώς η απόδειξή σου δεν είναι σωστή, καθώς δεν αποδεικνύεις έστω τις δύο από τις κυριότερες ιδιότητες του ζητούμενου δεκαπλεύρου, που είναι οι παράγραφοι (γ) και (ιβ).
Οι ιδιότητες των παραγράφων (α), (β), (δ), που μέχρι τώρα απέδειξες, αληθεύουν σε όλα τα δεκάπλευρα που έχουν συντρέχουσες διαγώνιες (κύριες). Τούτο σημαίνει ότι δεν έχουμε αγγίξει ακόμα τη λύση του προβλήματος.
Για την ιδιότητα της παραγράφου (γ), το πρόβλημα δε ζητά αυτό που απέδειξες μόνο, δηλαδή της πέντε ισότητες μεμονωμένα, αλλά και ότι αυτές πρέπει να είναι και μεταξύ τους ίσες. Γράφεις ότι για να συμβεί αυτό θα πρέπει οι πέντε πρώτες διαδοχικές πλευρές του δεκαπλεύρου να είναι ίσες, αλλά δε το δικαιολογείς.
Ειδικά την ιδιότητα της παραγράφου (ιβ), δεν την απέδειξες, όπως και τις υπόλοιπες παραγράφους από (ε) μέχρι (ιζ), που πρέπει να αποδειχθούν για να έχουμε επιτύχει λύση του προβλήματος και οι οποίες δεν είναι εύκολες όπως λες, αντίθετα αποτελούν τη δυσκολία του προβλήματος, μαζί με εκείνη της παραγράφου (γ).
Νίκος Δ. Κυριαζής
Λέξεις Κλειδιά:
-
ΝΙΚΟΣ
- Διακεκριμένο Μέλος
- Δημοσιεύσεις: 1888
- Εγγραφή: Παρ Νοέμ 13, 2009 8:35 pm
- Τοποθεσία: Καλαμαριά (Θεσσαλονίκη).
Re: ΓΕΩΜΕΤΡIΑ. ΠΡΩΤΟΕΜΦΑΝΙΖΟΜΕΝΕΣ ΠΡΟΤΑΣΕΙΣ.
Λύση του παραπάνω Προβλήματος ΓΙΓΑΣ Α44.
Αγαπητοί φίλοι,
Την πρώτη λύση μου, θα βρείτε, αν χρησιμοποιήσετε το σύνδεσμο:
https://parmenides52.blogspot.com/2016/ ... nikos.html
και στη συνέχεια ακολουθήσετε τη διαδρομή:
Βιβλίο «ΑΡΜΟΝΙΚΗ ΓΕΩΜΕΤΡΙΑ», Σελίδα βιβλίου από 692 μέχρι 700 , ή διαδικτυακά από 694 μέχρι 702, Κατασκευή 203.
Τη δεύτερη λύση μου, την έχω αναρτήσει ήδη με την εκφώνηση του Προβλήματος (Ποστ 375).
Ή, πιο εύκολα, τη λύση μου θα βρείτε αν πάτε στο σύνδεσμο:
https://drive.google.com/file/d/0B9uh0V ... 3fonbUWkMQ
και στη συνέχεια ακολουθήσετε τη διαδρομή: Σελίδα βιβλίου από 692 μέχρι 700 , ή διαδικτυακά από 694 μέχρι 702, Κατασκευή 203.
Παρακαλώ για τις δικές σας λ/υσεις και για τα καλοπροαίρετα σχετικά σχόλιά σας.
Αγαπητοί φίλοι, και για την παραπάνω Πρόταση, παρακαλώ όπως οι ενδεχόμενες απαντήσεις σας, να είναι πάντα μέσα στο παραπάνω αναφερόμενο πνεύμα του ποστ 1, για να αποφεύγονται παρεξηγήσεις.
Σχόλια
(α). Εξακολουθεί να ισχύει και η παρακάτω απάντησή μου του ποστ 378:
Επί του παρόντος δε θα μπω σε λεπτομέρειες για να αποφανθώ ότι ατυχώς η απόδειξή σου Μιχ. Λάμπρου δεν είναι σωστή, καθώς δεν αποδεικνύεις έστω τις δύο από τις κυριότερες ιδιότητες του ζητούμενου δεκαπλεύρου, που είναι οι παράγραφοι (γ) και (ιβ).
Οι ιδιότητες των παραγράφων (α), (β), (δ), που μέχρι τώρα απέδειξες, αληθεύουν σε όλα τα δεκάπλευρα που έχουν συντρέχουσες διαγώνιες (κύριες). Τούτο σημαίνει ότι δεν έχουμε αγγίξει ακόμα τη λύση του προβλήματος.
Για την ιδιότητα της παραγράφου (γ), το πρόβλημα δε ζητά αυτό που απέδειξες μόνο, δηλαδή της πέντε ισότητες μεμονωμένα, αλλά και ότι αυτές πρέπει να είναι και μεταξύ τους ίσες. Γράφεις ότι για να συμβεί αυτό θα πρέπει οι πέντε πρώτες διαδοχικές πλευρές του δεκαπλεύρου να είναι ίσες, αλλά δε το δικαιολογείς.
Ειδικά την ιδιότητα της παραγράφου (ιβ), δεν την απέδειξες, όπως και τις υπόλοιπες παραγράφους από (ε) μέχρι (ιζ), που πρέπει να αποδειχθούν για να έχουμε επιτύχει λύση του προβλήματος και οι οποίες δεν είναι εύκολες όπως λες, αντίθετα αποτελούν τη δυσκολία του προβλήματος, μαζί με εκείνη της παραγράφου (γ)».
(β). Το δοσμένο πρόβλημα στην ουσία είναι η κατασκευή αρμονικού δεκάγωνου (Του οποίου ορισμοί, επεξηγήσεις, πληροφορίες και λεπτομερή σχήματα δίνονται στον παρακάτω σύνδεσμο) και μόνο για το οποίο (αρμονικό δεκάγωνο) αληθεύουν και οι 17 ιδιότητες του δοσμένου προβλήματος.
Το ερώτημά μου είναι:
Έχει κάποια σχέση η παραπάνω δοσμένη λύση και τα σχήματά της του κ. Μ. Λάμπρου, με όλα αυτά που αναφέρονται στο δοσμένο πρόβλημα του παρακάτω συνδέσμου, ή με το δεκάγωνο των παραπάνω δικών μου λύσεων; Η διαπίστωση μπορεί να γίνει μόνο με μια ματιά.
Θα ήθελα την απάντηση εκείνων που αγαπούν τη Γεωμετρία και που δε θέλουν να την βλέουν να ποδο-πατιέται.
https://drive.google.com/file/d/1MA40GS ... HEp3s/view
Φιλικά και ταπεινά.
Νίκος Κυριαζής.
Είμαστε ότι επιλέγουμε.
Αγαπητοί φίλοι,
Την πρώτη λύση μου, θα βρείτε, αν χρησιμοποιήσετε το σύνδεσμο:
https://parmenides52.blogspot.com/2016/ ... nikos.html
και στη συνέχεια ακολουθήσετε τη διαδρομή:
Βιβλίο «ΑΡΜΟΝΙΚΗ ΓΕΩΜΕΤΡΙΑ», Σελίδα βιβλίου από 692 μέχρι 700 , ή διαδικτυακά από 694 μέχρι 702, Κατασκευή 203.
Τη δεύτερη λύση μου, την έχω αναρτήσει ήδη με την εκφώνηση του Προβλήματος (Ποστ 375).
Ή, πιο εύκολα, τη λύση μου θα βρείτε αν πάτε στο σύνδεσμο:
https://drive.google.com/file/d/0B9uh0V ... 3fonbUWkMQ
και στη συνέχεια ακολουθήσετε τη διαδρομή: Σελίδα βιβλίου από 692 μέχρι 700 , ή διαδικτυακά από 694 μέχρι 702, Κατασκευή 203.
Παρακαλώ για τις δικές σας λ/υσεις και για τα καλοπροαίρετα σχετικά σχόλιά σας.
Αγαπητοί φίλοι, και για την παραπάνω Πρόταση, παρακαλώ όπως οι ενδεχόμενες απαντήσεις σας, να είναι πάντα μέσα στο παραπάνω αναφερόμενο πνεύμα του ποστ 1, για να αποφεύγονται παρεξηγήσεις.
Σχόλια
(α). Εξακολουθεί να ισχύει και η παρακάτω απάντησή μου του ποστ 378:
Επί του παρόντος δε θα μπω σε λεπτομέρειες για να αποφανθώ ότι ατυχώς η απόδειξή σου Μιχ. Λάμπρου δεν είναι σωστή, καθώς δεν αποδεικνύεις έστω τις δύο από τις κυριότερες ιδιότητες του ζητούμενου δεκαπλεύρου, που είναι οι παράγραφοι (γ) και (ιβ).
Οι ιδιότητες των παραγράφων (α), (β), (δ), που μέχρι τώρα απέδειξες, αληθεύουν σε όλα τα δεκάπλευρα που έχουν συντρέχουσες διαγώνιες (κύριες). Τούτο σημαίνει ότι δεν έχουμε αγγίξει ακόμα τη λύση του προβλήματος.
Για την ιδιότητα της παραγράφου (γ), το πρόβλημα δε ζητά αυτό που απέδειξες μόνο, δηλαδή της πέντε ισότητες μεμονωμένα, αλλά και ότι αυτές πρέπει να είναι και μεταξύ τους ίσες. Γράφεις ότι για να συμβεί αυτό θα πρέπει οι πέντε πρώτες διαδοχικές πλευρές του δεκαπλεύρου να είναι ίσες, αλλά δε το δικαιολογείς.
Ειδικά την ιδιότητα της παραγράφου (ιβ), δεν την απέδειξες, όπως και τις υπόλοιπες παραγράφους από (ε) μέχρι (ιζ), που πρέπει να αποδειχθούν για να έχουμε επιτύχει λύση του προβλήματος και οι οποίες δεν είναι εύκολες όπως λες, αντίθετα αποτελούν τη δυσκολία του προβλήματος, μαζί με εκείνη της παραγράφου (γ)».
(β). Το δοσμένο πρόβλημα στην ουσία είναι η κατασκευή αρμονικού δεκάγωνου (Του οποίου ορισμοί, επεξηγήσεις, πληροφορίες και λεπτομερή σχήματα δίνονται στον παρακάτω σύνδεσμο) και μόνο για το οποίο (αρμονικό δεκάγωνο) αληθεύουν και οι 17 ιδιότητες του δοσμένου προβλήματος.
Το ερώτημά μου είναι:
Έχει κάποια σχέση η παραπάνω δοσμένη λύση και τα σχήματά της του κ. Μ. Λάμπρου, με όλα αυτά που αναφέρονται στο δοσμένο πρόβλημα του παρακάτω συνδέσμου, ή με το δεκάγωνο των παραπάνω δικών μου λύσεων; Η διαπίστωση μπορεί να γίνει μόνο με μια ματιά.
Θα ήθελα την απάντηση εκείνων που αγαπούν τη Γεωμετρία και που δε θέλουν να την βλέουν να ποδο-πατιέται.
https://drive.google.com/file/d/1MA40GS ... HEp3s/view
Φιλικά και ταπεινά.
Νίκος Κυριαζής.
Είμαστε ότι επιλέγουμε.
-
ΝΙΚΟΣ
- Διακεκριμένο Μέλος
- Δημοσιεύσεις: 1888
- Εγγραφή: Παρ Νοέμ 13, 2009 8:35 pm
- Τοποθεσία: Καλαμαριά (Θεσσαλονίκη).
Re: ΓΕΩΜΕΤΡIΑ. ΠΡΩΤΟΕΜΦΑΝΙΖΟΜΕΝΕΣ ΠΡΟΤΑΣΕΙΣ.
Νέα Πρόταση Γεωμετρίας.
Τρία ισόπλευρα τρίγωνα - Πέντε τρίγωνα με κοινό βαρύκεντρο.
Αγαπητοί φίλοι,
προτείνω για απόδειξη την παρακάτω νέα Πρόταση Γεωμετρίας. Α45:
Α45. Θεωρούμε κανονικό εξάγωνο ,
,  ,
,  ,...,
,...,  , τα μέσα των πλευρών του
, τα μέσα των πλευρών του  ,
,  ,…,
,…, , αντίστοιχα,
, αντίστοιχα, 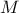 ,
,  ,
,  ,
,  ,
,  , τα μέσα των
, τα μέσα των  ,
,  ,
,  ,
,  ,
,  και
και  τον περιγεγραμμένο κύκλο του εξάγωνου.
τον περιγεγραμμένο κύκλο του εξάγωνου.
1. Να δειχθεί ότι:
(α). Τα τρία τρίγωνα ,
, 
 , είναι ισόπλευρα.
, είναι ισόπλευρα.
(β). Οι δύο τριάδες ευθειών ,
,  ,
,  και
και  ,
,  ,
,  συντρέχουν, κατά τριάδες.
συντρέχουν, κατά τριάδες.
(γ). Τα πέντε τρίγωνα ,
, 
 ,
,  ,
,  έχουν κοινό βαρύκεντρο.
έχουν κοινό βαρύκεντρο.
2. Ακόμη να εντοπισθεί και να αναφερθεί η πραγματική αιτία που αληθεύουν όλα τα παραπάνω ζητούμενα.
Παρακαλώ για τις νέες δικές σας αποδείξεις και για τα σχετικά καλοπροαίρετα σχόλιά σας.
Δική μου απόδειξη, θα ακολουθήσει σε εύλογο χρονικό διάστημα.
Βασιζόμενοι στη παραπάνω Άσκηση, θα μας είναι εύκολη και η απόδειξη-λύση σχετικών Προτάσεων και Προβλημάτων, τα οποία θα μας δίνονται μελλοντικά, αυτός είναι άλλωστε και ο λόγος που την επινόησα.
Αγαπητοί φίλοι, και για την παραπάνω κατασκευή, παρακαλώ οι ενδεχόμενες απαντήσεις σας, να είναι πάντα μέσα στο παραπάνω αναφερόμενο πνεύμα του ποστ 1, για να αποφεύγονται παρεξηγήσεις.
Φιλικά και Ταπεινά
Νίκος Κυριαζής
Από όσα γράφονται εδώ στο mathematica, αποδεικνύεται, για μια φορά ακόμη,ότι η Γεωμετρία ζει και αναπτύσσεται, σε πείσμα των εχθρών της.
Τρία ισόπλευρα τρίγωνα - Πέντε τρίγωνα με κοινό βαρύκεντρο.
Αγαπητοί φίλοι,
προτείνω για απόδειξη την παρακάτω νέα Πρόταση Γεωμετρίας. Α45:
Α45. Θεωρούμε κανονικό εξάγωνο
 ,
,  ,
,  ,...,
,...,  , τα μέσα των πλευρών του
, τα μέσα των πλευρών του  ,
,  ,…,
,…, , αντίστοιχα,
, αντίστοιχα, 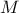 ,
,  ,
,  ,
,  ,
,  , τα μέσα των
, τα μέσα των  ,
,  ,
,  ,
,  ,
,  και
και  τον περιγεγραμμένο κύκλο του εξάγωνου.
τον περιγεγραμμένο κύκλο του εξάγωνου. 1. Να δειχθεί ότι:
(α). Τα τρία τρίγωνα
 ,
, 
 , είναι ισόπλευρα.
, είναι ισόπλευρα.(β). Οι δύο τριάδες ευθειών
 ,
,  ,
,  και
και  ,
,  ,
,  συντρέχουν, κατά τριάδες.
συντρέχουν, κατά τριάδες.(γ). Τα πέντε τρίγωνα
 ,
, 
 ,
,  ,
,  έχουν κοινό βαρύκεντρο.
έχουν κοινό βαρύκεντρο.2. Ακόμη να εντοπισθεί και να αναφερθεί η πραγματική αιτία που αληθεύουν όλα τα παραπάνω ζητούμενα.
Παρακαλώ για τις νέες δικές σας αποδείξεις και για τα σχετικά καλοπροαίρετα σχόλιά σας.
Δική μου απόδειξη, θα ακολουθήσει σε εύλογο χρονικό διάστημα.
Βασιζόμενοι στη παραπάνω Άσκηση, θα μας είναι εύκολη και η απόδειξη-λύση σχετικών Προτάσεων και Προβλημάτων, τα οποία θα μας δίνονται μελλοντικά, αυτός είναι άλλωστε και ο λόγος που την επινόησα.
Αγαπητοί φίλοι, και για την παραπάνω κατασκευή, παρακαλώ οι ενδεχόμενες απαντήσεις σας, να είναι πάντα μέσα στο παραπάνω αναφερόμενο πνεύμα του ποστ 1, για να αποφεύγονται παρεξηγήσεις.
Φιλικά και Ταπεινά
Νίκος Κυριαζής
Από όσα γράφονται εδώ στο mathematica, αποδεικνύεται, για μια φορά ακόμη,ότι η Γεωμετρία ζει και αναπτύσσεται, σε πείσμα των εχθρών της.
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 17550
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: ΓΕΩΜΕΤΡIΑ. ΠΡΩΤΟΕΜΦΑΝΙΖΟΜΕΝΕΣ ΠΡΟΤΑΣΕΙΣ.
. .ΝΙΚΟΣ έγραψε: ↑Παρ Οκτ 24, 2025 1:50 pmΑ45. Θεωρούμε κανονικό εξάγωνο,
,
,...,
, τα μέσα των πλευρών του
,
,…,
, αντίστοιχα,
,
,
,
,
, τα μέσα των
,
,
,
,
και
τον περιγεγραμμένο κύκλο του εξάγωνου.
1. Να δειχθεί ότι:
(α). Τα τρία τρίγωνα,

, είναι ισόπλευρα.
(β). Οι δύο τριάδες ευθειών,
,
και
,
,
συντρέχουν, κατά τριάδες.
(γ). Τα πέντε τρίγωνα,

,
,
έχουν κοινό βαρύκεντρο.
2. Ακόμη να εντοπισθεί και να αναφερθεί η πραγματική αιτία που αληθεύουν όλα τα παραπάνω ζητούμενα.
Υπάρχει λύση καθαρά Ευκλείδεια αλλά θα κάνω μία με Αναλυτική Γεωμετρία για δύο λόγους. Πρώτον οι αποδείξεις είναι άμεσες (δεν χρειάζονται σκέψη) και δεύτερον και κυριότερο βγαίνει αμέσως μία πληθώρα άλλων ιδιοτήτων που δεν είναι εύκολα ορατές με Ευκλείδεια. Για αυτό το τελευταίο δίνω δύο παραδείγματα.
Πρώτο: Το σημείο
 που ορίζεται ως το μέσον της
που ορίζεται ως το μέσον της  αποδεικνύεται ότι είναι επίσης σημείο του
αποδεικνύεται ότι είναι επίσης σημείο του  και μάλιστα το χωρίζει σε λόγο
και μάλιστα το χωρίζει σε λόγο  , εδώ
, εδώ  .
.Δεύτερο: Τα συντρέχοντα (στο
 ) τμήματα
) τμήματα  διαιρούνται από το
διαιρούνται από το  σε λόγους
σε λόγους  αντίστοιχα, δηλαδή
αντίστοιχα, δηλαδή  και
και  .
. Ας έλθουμε στα ζητούμενα. Παίρνοντας όμοιο εξάγωνο μπορούμε να υποθέσουμε ότι ο κύκλος που το περιέχει έχει ακτίνα
 , και το κέντρο του ως προς άξονες είναι το
, και το κέντρο του ως προς άξονες είναι το  . Χρησιμοποιώντας τα
. Χρησιμοποιώντας τα  εύκολα διαπιστώνουμε τις συντεταγμένες
εύκολα διαπιστώνουμε τις συντεταγμένες 
Τώρα τα μέσα τους είναι άμεσα, και συγκεκριμένα είναι

Επίσης είναι τώρα άμεσα τα μέσα
 . Συγκεκριμένα
. Συγκεκριμένα 
Έρχομαι τώρα στις αποδείξεις:
α) Από τις παραπάνω συντεταγμένες το τρίγωνο
 έχει πλευρές μήκους
έχει πλευρές μήκους  και
και  και
και 
Με άλλα λόγια είναι ισόπλευρο με πλευρά μήκους
 . Όμοια τα άλλα δύο τρίγωνα, και συγκεκριμένα έχουν πλευρές
. Όμοια τα άλλα δύο τρίγωνα, και συγκεκριμένα έχουν πλευρές  και
και  , αντίστοιχα.
, αντίστοιχα.β) Για να δείξουμε ότι οι
 είναι συντρέχουσες θα δείξουμε ότι το σημείο
είναι συντρέχουσες θα δείξουμε ότι το σημείο  βρίσκεται και στις τρεις, και μάλιστα τις διαιρεί σε λόγους
βρίσκεται και στις τρεις, και μάλιστα τις διαιρεί σε λόγους  αντίστοιχα, δηλαδή
αντίστοιχα, δηλαδή  και
και  (όπως σημείωσα παραπάνω). Για τον σκοπό αυτό θα χρησιμοποιήσω το γεγονός ότι το σημείο που διαιρεί ένα τμήμα
(όπως σημείωσα παραπάνω). Για τον σκοπό αυτό θα χρησιμοποιήσω το γεγονός ότι το σημείο που διαιρεί ένα τμήμα  σε λόγο
σε λόγο  , όπου
, όπου  είναι το
είναι το  . Πράγματι βλέπουμε αμέσως ότι το
. Πράγματι βλέπουμε αμέσως ότι το  δίνει το σημείο
δίνει το σημείο  και όμοια
και όμοια  και
και  δίνουν ακριβώς το ίδιο σημείο. Αυτό ολοκληρώνει το ζητούμενο. Όμοια η δεύτερη σύκλιση.
δίνουν ακριβώς το ίδιο σημείο. Αυτό ολοκληρώνει το ζητούμενο. Όμοια η δεύτερη σύκλιση.γ) Μένουν τα κέντα βάρους. Εδώ θα χρησιμοποιήσω ότι το κέντρο βάρους ενός τριγώνου
 όπου
όπου  είναι το
είναι το  . Με αυτό κατά νου εύκολα βλέπουμε ότι το κέντρο βάρους καθενός από τα πέντε τρίγωνα
. Με αυτό κατά νου εύκολα βλέπουμε ότι το κέντρο βάρους καθενός από τα πέντε τρίγωνα  ,
, 
 ,
,  ,
,  είναι το σημείο
είναι το σημείο  (άμεσο). Για παράδειγμα το
(άμεσο). Για παράδειγμα το  έχει
έχει  , άρα έχει κέντρο βάρους
, άρα έχει κέντρο βάρους  .
.Όμοια τα υπόλοιπα. Αυτό ολοκληρώνει την απόδειξη.
-
ΝΙΚΟΣ
- Διακεκριμένο Μέλος
- Δημοσιεύσεις: 1888
- Εγγραφή: Παρ Νοέμ 13, 2009 8:35 pm
- Τοποθεσία: Καλαμαριά (Θεσσαλονίκη).
Re: ΓΕΩΜΕΤΡIΑ. ΠΡΩΤΟΕΜΦΑΝΙΖΟΜΕΝΕΣ ΠΡΟΤΑΣΕΙΣ.
Αποδείξεις της παραπάνω Πρότασης Α46..
Αγαπητοί φίλοι,
Δύο αποδείξεις μου, θα βρείτε, αν πάτε στο σύνδεσμο:
https://parmenides52.blogspot.com/2016/ ... nikos.html
και στη συνέχεια ακολουθήσετε τη διαδρομή:
Βιβλίο Νέα Στοιχεία Γεωμετρίας Τεύχος 5, Σελίδα βιβλίου 32, ή διαδικτυακά 38 Πρόταση 5θ(26).
Ή, πιο εύκολα, τις αποδείξεις μου θα βρείτε αν πάτε στο σύνδεσμο:
https://drive.google.com/file/d/1mN4NkD ... lDa4z/view
και στη συνέχεια ακολουθήσετε τη διαδρομή: Σελίδα βιβλίου 32, ή ψηφιακά 38, παράγραφος 5θ(26).
Παρακαλώ για τις δικές σας αποδείξεις και για τα καλοπροαίρετα σχετικά σχόλιά σας.
Αγαπητοί φίλοι, και για την παραπάνω Πρόταση, παρακαλώ όπως οι ενδεχόμενες απαντήσεις σας, να είναι πάντα μέσα στο παραπάνω αναφερόμενο πνεύμα του ποστ 1, για να αποφεύγονται παρεξηγήσεις.
Φιλικά και ταπεινά.
Νίκος Κυριαζής.
/b Η Ευκλείδεια Γεωμετρία: Αποτελεί κατεξοχήν Ελληνική Επιστήμη, καθώς πρώτος ο Θαλής την θεμελίωσε ως Επιστήμη, εισάγοντας την απόδειξη και ακολούθησε ο Ευκλείδης με το διαχρονικό και ανεπανάληπτο έργο του, τα "ΣΤΟΙΧΕΙΑ". Έτσι, με βάσει την απόδειξη, ξεκίνησε η ανάπτυξη και των άλλων επιστημών.]
Αγαπητοί φίλοι,
Δύο αποδείξεις μου, θα βρείτε, αν πάτε στο σύνδεσμο:
https://parmenides52.blogspot.com/2016/ ... nikos.html
και στη συνέχεια ακολουθήσετε τη διαδρομή:
Βιβλίο Νέα Στοιχεία Γεωμετρίας Τεύχος 5, Σελίδα βιβλίου 32, ή διαδικτυακά 38 Πρόταση 5θ(26).
Ή, πιο εύκολα, τις αποδείξεις μου θα βρείτε αν πάτε στο σύνδεσμο:
https://drive.google.com/file/d/1mN4NkD ... lDa4z/view
και στη συνέχεια ακολουθήσετε τη διαδρομή: Σελίδα βιβλίου 32, ή ψηφιακά 38, παράγραφος 5θ(26).
Παρακαλώ για τις δικές σας αποδείξεις και για τα καλοπροαίρετα σχετικά σχόλιά σας.
Αγαπητοί φίλοι, και για την παραπάνω Πρόταση, παρακαλώ όπως οι ενδεχόμενες απαντήσεις σας, να είναι πάντα μέσα στο παραπάνω αναφερόμενο πνεύμα του ποστ 1, για να αποφεύγονται παρεξηγήσεις.
Φιλικά και ταπεινά.
Νίκος Κυριαζής.
/b Η Ευκλείδεια Γεωμετρία: Αποτελεί κατεξοχήν Ελληνική Επιστήμη, καθώς πρώτος ο Θαλής την θεμελίωσε ως Επιστήμη, εισάγοντας την απόδειξη και ακολούθησε ο Ευκλείδης με το διαχρονικό και ανεπανάληπτο έργο του, τα "ΣΤΟΙΧΕΙΑ". Έτσι, με βάσει την απόδειξη, ξεκίνησε η ανάπτυξη και των άλλων επιστημών.]
τελευταία επεξεργασία από ΝΙΚΟΣ σε Τρί Νοέμ 18, 2025 11:10 am, έχει επεξεργασθεί 1 φορά συνολικά.
-
ΝΙΚΟΣ
- Διακεκριμένο Μέλος
- Δημοσιεύσεις: 1888
- Εγγραφή: Παρ Νοέμ 13, 2009 8:35 pm
- Τοποθεσία: Καλαμαριά (Θεσσαλονίκη).
Re: ΓΕΩΜΕΤΡIΑ. ΠΡΩΤΟΕΜΦΑΝΙΖΟΜΕΝΕΣ ΠΡΟΤΑΣΕΙΣ.
Νέα Πρόταση Γεωμετρίας.
Αγαπητοί φίλοι,
προτείνω για απόδειξη την παρακάτω νέα Πρόταση Γεωμετρίας. Α46:
Α46. Θεωρούμε ισοσκελές τρίγωνο
 και τις παράλληλες
και τις παράλληλες  ,
, 
 , από σημείο
, από σημείο  της βάσεως του ως προς τις πλευρές
της βάσεως του ως προς τις πλευρές  ,
,  αντίστοιχα. Αν
αντίστοιχα. Αν  , να αποδειχθεί ότι η
, να αποδειχθεί ότι η  είναι συμμετροδΙάμεσος του τριγώνου
είναι συμμετροδΙάμεσος του τριγώνου 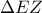 .
.
Παρακαλώ για τις νέες δικές σας αποδείξεις και για τα σχετικά καλοπροαίρετα σχόλιά σας.
Δική μου απόδειξη, θα ακολουθήσει σε εύλογο χρονικό διάστημα.
Βασιζόμενοι στη παραπάνω Άσκηση, θα μας είναι εύκολη και η απόδειξη-λύση σχετικών Προτάσεων και Προβλημάτων, τα οποία θα μας δίνονται μελλοντικά, αυτός είναι άλλωστε και ο λόγος που την επινόησα.
Αγαπητοί φίλοι, και για την παραπάνω κατασκευή, παρακαλώ οι ενδεχόμενες απαντήσεις σας, να είναι πάντα μέσα στο παραπάνω αναφερόμενο πνεύμα του ποστ 1, για να αποφεύγονται παρεξηγήσεις.
Φιλικά
Νίκος Κυριαζής
Είμαστε, ο,τι αφήνουμε πίσω μας ” :
https://parmenides52.blogspot.com/2016/ ... nikos.html

Αγαπητοί φίλοι,
προτείνω για απόδειξη την παρακάτω νέα Πρόταση Γεωμετρίας. Α46:
Α46. Θεωρούμε ισοσκελές τρίγωνο

 και τις παράλληλες
και τις παράλληλες  ,
, 
 , από σημείο
, από σημείο  της βάσεως του ως προς τις πλευρές
της βάσεως του ως προς τις πλευρές  ,
,  αντίστοιχα. Αν
αντίστοιχα. Αν  , να αποδειχθεί ότι η
, να αποδειχθεί ότι η  είναι συμμετροδΙάμεσος του τριγώνου
είναι συμμετροδΙάμεσος του τριγώνου 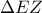 .
. Παρακαλώ για τις νέες δικές σας αποδείξεις και για τα σχετικά καλοπροαίρετα σχόλιά σας.
Δική μου απόδειξη, θα ακολουθήσει σε εύλογο χρονικό διάστημα.
Βασιζόμενοι στη παραπάνω Άσκηση, θα μας είναι εύκολη και η απόδειξη-λύση σχετικών Προτάσεων και Προβλημάτων, τα οποία θα μας δίνονται μελλοντικά, αυτός είναι άλλωστε και ο λόγος που την επινόησα.
Αγαπητοί φίλοι, και για την παραπάνω κατασκευή, παρακαλώ οι ενδεχόμενες απαντήσεις σας, να είναι πάντα μέσα στο παραπάνω αναφερόμενο πνεύμα του ποστ 1, για να αποφεύγονται παρεξηγήσεις.
Φιλικά
Νίκος Κυριαζής
Είμαστε, ο,τι αφήνουμε πίσω μας ” :
https://parmenides52.blogspot.com/2016/ ... nikos.html
-
ΝΙΚΟΣ
- Διακεκριμένο Μέλος
- Δημοσιεύσεις: 1888
- Εγγραφή: Παρ Νοέμ 13, 2009 8:35 pm
- Τοποθεσία: Καλαμαριά (Θεσσαλονίκη).
Re: ΓΕΩΜΕΤΡIΑ. ΠΡΩΤΟΕΜΦΑΝΙΖΟΜΕΝΕΣ ΠΡΟΤΑΣΕΙΣ.
Αποδείξεις της παραπάνω Πρότασης Α46..
Αγαπητοί φίλοι,
Δύο αποδείξεις μου, θα βρείτε, αν πάτε στο σύνδεσμο:
https://parmenides52.blogspot.com/2016/ ... nikos.html
και στη συνέχεια ακολουθήσετε τη διαδρομή:
Βιβλίο Νέα Στοιχεία Γεωμετρίας Τεύχος 5, Σελίδα βιβλίου 32, ή διαδικτυακά 38 Πρόταση 5θ(26).
Ή, πιο εύκολα, τις αποδείξεις μου θα βρείτε αν πάτε στο σύνδεσμο:
https://drive.google.com/file/d/1mN4NkD ... lDa4z/view
και στη συνέχεια ακολουθήσετε τη διαδρομή: Σελίδα βιβλίου 32, ή ψηφιακά 38, παράγραφος 5θ(26).
Παρακαλώ για τις δικές σας αποδείξεις και για τα καλοπροαίρετα σχετικά σχόλιά σας.
Αγαπητοί φίλοι, και για την παραπάνω Πρόταση, παρακαλώ όπως οι ενδεχόμενες απαντήσεις σας, να είναι πάντα μέσα στο παραπάνω αναφερόμενο πνεύμα του ποστ 1, για να αποφεύγονται παρεξηγήσεις.
Φιλικά και ταπεινά.
Νίκος Κυριαζής.
/b Η Ευκλείδεια Γεωμετρία: Αποτελεί κατεξοχήν Ελληνική Επιστήμη, καθώς πρώτος ο Θαλής την θεμελίωσε ως Επιστήμη, εισάγοντας την απόδειξη και ακολούθησε ο Ευκλείδης με το διαχρονικό και ανεπανάληπτο έργο του, τα "ΣΤΟΙΧΕΙΑ". Έτσι, με βάσει την απόδειξη, ξεκίνησε η ανάπτυξη και των άλλων επιστημών.]
Αγαπητοί φίλοι,
Δύο αποδείξεις μου, θα βρείτε, αν πάτε στο σύνδεσμο:
https://parmenides52.blogspot.com/2016/ ... nikos.html
και στη συνέχεια ακολουθήσετε τη διαδρομή:
Βιβλίο Νέα Στοιχεία Γεωμετρίας Τεύχος 5, Σελίδα βιβλίου 32, ή διαδικτυακά 38 Πρόταση 5θ(26).
Ή, πιο εύκολα, τις αποδείξεις μου θα βρείτε αν πάτε στο σύνδεσμο:
https://drive.google.com/file/d/1mN4NkD ... lDa4z/view
και στη συνέχεια ακολουθήσετε τη διαδρομή: Σελίδα βιβλίου 32, ή ψηφιακά 38, παράγραφος 5θ(26).
Παρακαλώ για τις δικές σας αποδείξεις και για τα καλοπροαίρετα σχετικά σχόλιά σας.
Αγαπητοί φίλοι, και για την παραπάνω Πρόταση, παρακαλώ όπως οι ενδεχόμενες απαντήσεις σας, να είναι πάντα μέσα στο παραπάνω αναφερόμενο πνεύμα του ποστ 1, για να αποφεύγονται παρεξηγήσεις.
Φιλικά και ταπεινά.
Νίκος Κυριαζής.
/b Η Ευκλείδεια Γεωμετρία: Αποτελεί κατεξοχήν Ελληνική Επιστήμη, καθώς πρώτος ο Θαλής την θεμελίωσε ως Επιστήμη, εισάγοντας την απόδειξη και ακολούθησε ο Ευκλείδης με το διαχρονικό και ανεπανάληπτο έργο του, τα "ΣΤΟΙΧΕΙΑ". Έτσι, με βάσει την απόδειξη, ξεκίνησε η ανάπτυξη και των άλλων επιστημών.]
-
ΝΙΚΟΣ
- Διακεκριμένο Μέλος
- Δημοσιεύσεις: 1888
- Εγγραφή: Παρ Νοέμ 13, 2009 8:35 pm
- Τοποθεσία: Καλαμαριά (Θεσσαλονίκη).
Re: ΓΕΩΜΕΤΡIΑ. ΠΡΩΤΟΕΜΦΑΝΙΖΟΜΕΝΕΣ ΠΡΟΤΑΣΕΙΣ.
Νέα Πρόταση Γεωμετρίας.
Αγαπητοί φίλοι,
προτείνω για απόδειξη την παρακάτω νέα Πρόταση Γεωμετρίας. Α47:
Α47. Σε κάθε πλήρες τετράπλευρο, οι τρεις ευθείες που συνδέουν το σημείο Miquel με τις τρεις κορυφές του που βρίσκονται σε κάθε μια από τις πλευρές του, είναι ισοκλινείς με τις τρεις υπόλοιπες πλευρές του.
Παρακαλώ για τις νέες δικές σας αποδείξεις και για τα σχετικά καλοπροαίρετα σχόλιά σας.
Δική μου απόδειξη, θα ακολουθήσει σε εύλογο χρονικό διάστημα.
Βασιζόμενοι στη παραπάνω Άσκηση, θα μας είναι εύκολη και η απόδειξη-λύση σχετικών Προτάσεων και Προβλημάτων, τα οποία θα μας δίνονται μελλοντικά, αυτός είναι άλλωστε και ο λόγος που την επινόησα.
Αγαπητοί φίλοι, και για την παραπάνω κατασκευή, παρακαλώ οι ενδεχόμενες απαντήσεις σας, να είναι πάντα μέσα στο παραπάνω αναφερόμενο πνεύμα του ποστ 1, για να αποφεύγονται παρεξηγήσεις.
Φιλικά
Νίκος Κυριαζής
Ο Πούσκιν έλεγε ότι «Η έμπνευση στην Γεωμετρία, είναι το ίδιο απαραίτητη, όσο και στην ποίηση».
Αγαπητοί φίλοι,
προτείνω για απόδειξη την παρακάτω νέα Πρόταση Γεωμετρίας. Α47:
Α47. Σε κάθε πλήρες τετράπλευρο, οι τρεις ευθείες που συνδέουν το σημείο Miquel με τις τρεις κορυφές του που βρίσκονται σε κάθε μια από τις πλευρές του, είναι ισοκλινείς με τις τρεις υπόλοιπες πλευρές του.
Παρακαλώ για τις νέες δικές σας αποδείξεις και για τα σχετικά καλοπροαίρετα σχόλιά σας.
Δική μου απόδειξη, θα ακολουθήσει σε εύλογο χρονικό διάστημα.
Βασιζόμενοι στη παραπάνω Άσκηση, θα μας είναι εύκολη και η απόδειξη-λύση σχετικών Προτάσεων και Προβλημάτων, τα οποία θα μας δίνονται μελλοντικά, αυτός είναι άλλωστε και ο λόγος που την επινόησα.
Αγαπητοί φίλοι, και για την παραπάνω κατασκευή, παρακαλώ οι ενδεχόμενες απαντήσεις σας, να είναι πάντα μέσα στο παραπάνω αναφερόμενο πνεύμα του ποστ 1, για να αποφεύγονται παρεξηγήσεις.
Φιλικά
Νίκος Κυριαζής
Ο Πούσκιν έλεγε ότι «Η έμπνευση στην Γεωμετρία, είναι το ίδιο απαραίτητη, όσο και στην ποίηση».
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης
