Με μερική χρήση ομοιοθεσίας και αντιστροφής

- Μία ιδιότητα στο ισοσκελές τραπέζιο.jpg (50.25 KiB) Προβλήθηκε 561 φορές
(α) σχήμα 1
Οι κύκλοι

είναι ομοιόθετοι με κέντρο ομοιοθεσίας το σημείο

(υπάρχει ομοιοθεσία των παράλληλων διαμέτρων

), άρα

. Τότε

(λόγω παραλλήλων) και

(εγγεγραμμένες στο ίδιο τόξο) και

(λόγω συμμετρίας). Άρα

.
(β) σχήμα 2
Θεωρούμε την «μεγάλη» βάση

και την "μικρή"

. Τότε με απλές διαδικασίες (ομοιότητες τριγώνων) προκύπτει ότι

και

. Επίσης

, δηλαδή

, οπότε

, που συνδυασμό με την σχέση

προκύπτει

.
Οι κύκλοι

είναι ομοιόθετοι με κέντρο ομοιοθεσίας το σημείο

, άρα από το

άγεται κοινή εφαπτόμενη των

. Τότε υπάρχει αντιστροφή με πόλο το σημείο

και λόγο

ώστε οι

να αλληλοαντιστρέφονται. Επειδή το σημείο

μένει αμετάβλητο θα έχουμε

Όμως


, δηλαδή

, που σημαίνει ότι τα τρίγωνα

είναι όμοια και συνεπώς

.
Δεν κατάφερα να βρώ κομψότερη απόδειξη  Άλλες όμορφες παρατηρήσεις:
Άλλες όμορφες παρατηρήσεις:

- Μία ιδιότητα στο ισοσκελές τραπέζιο-2.jpg (29.21 KiB) Προβλήθηκε 561 φορές
1) Ισχύουν οι ισότητες γωνιών του σχήματος.
2) Επειδή έχουμε τα εξής αντίστροφα ζεύγη

κι’ επειδή η ευθεία

αντιστρέφεται σε κύκλο, έπεται ότι το τετράπλευρο

είναι εγγράψιμο.
3) Λόγω αντιστροφής τα τετράπλευρα

είναι εγγράψιμμα (και τα αντίστοιχα συμμετρικά τους)
 με
με  και έστω τα σημεία
και έστω τα σημεία  και
και  Με διαμέτρους τις βάσεις του
Με διαμέτρους τις βάσεις του 
 γράφουμε τους κύκλους
γράφουμε τους κύκλους 
 αντιστοίχως, οι οποίοι τέμνονται στα σημεία έστω
αντιστοίχως, οι οποίοι τέμνονται στα σημεία έστω 


 προς το αυτό μέρος της
προς το αυτό μέρος της 
 Αποδείξτε ότι
Αποδείξτε ότι  και
και  όπου
όπου  και
και  και
και 

 μεταξύ των
μεταξύ των 
 και
και  μεταξύ των
μεταξύ των 


 Καλή επιτυχία στα νιάτα του
Καλή επιτυχία στα νιάτα του 
 είναι ομοιόθετοι με κέντρο ομοιοθεσίας το σημείο
είναι ομοιόθετοι με κέντρο ομοιοθεσίας το σημείο  ), άρα
), άρα  . Τότε
. Τότε  (λόγω παραλλήλων) και
(λόγω παραλλήλων) και  (εγγεγραμμένες στο ίδιο τόξο) και
(εγγεγραμμένες στο ίδιο τόξο) και  (λόγω συμμετρίας). Άρα
(λόγω συμμετρίας). Άρα  .
. και την "μικρή"
και την "μικρή"  . Τότε με απλές διαδικασίες (ομοιότητες τριγώνων) προκύπτει ότι
. Τότε με απλές διαδικασίες (ομοιότητες τριγώνων) προκύπτει ότι  και
και  . Επίσης
. Επίσης  , δηλαδή
, δηλαδή  , οπότε
, οπότε  , που συνδυασμό με την σχέση
, που συνδυασμό με την σχέση  προκύπτει
προκύπτει  .
. ώστε οι
ώστε οι  μένει αμετάβλητο θα έχουμε
μένει αμετάβλητο θα έχουμε 

 , δηλαδή
, δηλαδή  , που σημαίνει ότι τα τρίγωνα
, που σημαίνει ότι τα τρίγωνα  είναι όμοια και συνεπώς
είναι όμοια και συνεπώς  .
. κι’ επειδή η ευθεία
κι’ επειδή η ευθεία  αντιστρέφεται σε κύκλο, έπεται ότι το τετράπλευρο
αντιστρέφεται σε κύκλο, έπεται ότι το τετράπλευρο  είναι εγγράψιμο.
είναι εγγράψιμο. είναι εγγράψιμμα (και τα αντίστοιχα συμμετρικά τους)
είναι εγγράψιμμα (και τα αντίστοιχα συμμετρικά τους)


 συμπεραίνεται ότι τα
συμπεραίνεται ότι τα  συνιστούν αρμονική σημειοσειρά, με εσωτερικό και εξωτερικό λόγο ίσο με τον λόγο των ακτίνων των κύκλων
συνιστούν αρμονική σημειοσειρά, με εσωτερικό και εξωτερικό λόγο ίσο με τον λόγο των ακτίνων των κύκλων 
 δηλαδή, ταυτίζονται με το εσωτερικό και το εξωτερικό κέντρο ομοιοθεσίας των δύο κύκλων, αντιστοίχως.
δηλαδή, ταυτίζονται με το εσωτερικό και το εξωτερικό κέντρο ομοιοθεσίας των δύο κύκλων, αντιστοίχως. είναι η εξής :
είναι η εξής : όπου
όπου 
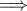




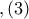

 και την αρμονικότητα των σημείων
και την αρμονικότητα των σημείων 
 είναι ίσα.
είναι ίσα. προφανώς το σημείο αυτό είναι το ομοιόθετο του
προφανώς το σημείο αυτό είναι το ομοιόθετο του  και επίσης το
και επίσης το  είναι το ομοιόθετο του
είναι το ομοιόθετο του  υπό την ίδια ομοιοθεσία.
υπό την ίδια ομοιοθεσία. ενώ
ενώ  και η απόδειξη ολοκληρώνεται αφού η ισότητα των γωνιών προκύπτει από την ισότητα των τόξων.γ
και η απόδειξη ολοκληρώνεται αφού η ισότητα των γωνιών προκύπτει από την ισότητα των τόξων.γ είναι αρμονικά συζυγή από θεωρία πλήρους τετραπλεύρου στο
είναι αρμονικά συζυγή από θεωρία πλήρους τετραπλεύρου στο  . Επίσης γνωρίζουμε από την ομοιοθεσία ότι
. Επίσης γνωρίζουμε από την ομοιοθεσία ότι  που σημαίνει ότι η
που σημαίνει ότι η  είναι εσωτερική και η
είναι εσωτερική και η  η εξωτερική διχοτόμος στο
η εξωτερική διχοτόμος στο  και άρα τέμνονται κάθετα.
και άρα τέμνονται κάθετα.