 . Εξωτερικά του τριγώνου αυτού κατασκευάζουμε τα τρίγωνα
. Εξωτερικά του τριγώνου αυτού κατασκευάζουμε τα τρίγωνα  και
και  , ώστε
, ώστε  ,
,  και
και  . Τα τμήματα
. Τα τμήματα  ,
,  τέμνονται στο σημείο
τέμνονται στο σημείο  . Έστω
. Έστω  το περίκεντρο του
το περίκεντρο του  . Να αποδειχτεί ότι
. Να αποδειχτεί ότι  .
.Συντονιστές: cretanman, Demetres, polysot, socrates, silouan, rek2
 . Εξωτερικά του τριγώνου αυτού κατασκευάζουμε τα τρίγωνα
. Εξωτερικά του τριγώνου αυτού κατασκευάζουμε τα τρίγωνα  και
και  , ώστε
, ώστε  ,
,  και
και  . Τα τμήματα
. Τα τμήματα  ,
,  τέμνονται στο σημείο
τέμνονται στο σημείο  . Έστω
. Έστω  το περίκεντρο του
το περίκεντρο του  . Να αποδειχτεί ότι
. Να αποδειχτεί ότι  .
. είναι το σημείο τομής των κύκλων
είναι το σημείο τομής των κύκλων  σχετικά εύκολα προκύπτει και από την προφανή ομοιότητα των συγκεκριμένων ισοσκελών τριγώνων ότι
σχετικά εύκολα προκύπτει και από την προφανή ομοιότητα των συγκεκριμένων ισοσκελών τριγώνων ότι 

 τα μέσα των χορδών
τα μέσα των χορδών  αντίστοιχα και
αντίστοιχα και  οι προβολές των κέντρων
οι προβολές των κέντρων  των κύκλων
των κύκλων  στις
στις  αντίστοιχα.
αντίστοιχα.

 καταλήξαμε από την εφαρμογή του 2ου θεωρήματος της διαμέσου. Στην εγγραψιμμότητα
καταλήξαμε από την εφαρμογή του 2ου θεωρήματος της διαμέσου. Στην εγγραψιμμότητα  καταλήξαμε από την ομοιότητα των ορθογωνίων τριγώνων
καταλήξαμε από την ομοιότητα των ορθογωνίων τριγώνων  .
. . Με τη στροφή κέντρου
. Με τη στροφή κέντρου  και γωνίας
και γωνίας  κατά τη θετική φορά (
κατά τη θετική φορά ( ), η εικόνα του
), η εικόνα του  είναι το
είναι το 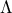 και του
και του  το
το  , οπότε
, οπότε 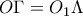 . Με τη στροφή κέντρου
. Με τη στροφή κέντρου  και γωνίας
και γωνίας  κατά την αρνητική φορά (
κατά την αρνητική φορά (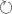 ), η εικόνα του
), η εικόνα του είναι το
είναι το  και του
και του  το
το  , οπότε
, οπότε  . Επειδή
. Επειδή  , τότε
, τότε  .
.  , οπότε το
, οπότε το 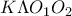 θα είναι παραλληλόγραμμο και το οποίο αποδεικνύει το ζητούμενο, αφού η
θα είναι παραλληλόγραμμο και το οποίο αποδεικνύει το ζητούμενο, αφού η  κάθετος της
κάθετος της  ως διχοτόμος στο ισοσκελές τρίγωνο
ως διχοτόμος στο ισοσκελές τρίγωνο  .
. και
και  είναι ίσα (
είναι ίσα ( και
και  ,
,  η γωνία του τριγώνου
η γωνία του τριγώνου  ), οπότε
), οπότε , δηλ. το
, δηλ. το  εγγράψιμο
εγγράψιμο , δηλ. το
, δηλ. το  επίσης εγγράψιμο.
επίσης εγγράψιμο.
 , οπότε
, οπότε  και άρα
και άρα  (επίκεντρη της παραπληρωματικής της
(επίκεντρη της παραπληρωματικής της  ).
). προκύπτει από το
προκύπτει από το  με την ακολουθία των επόμενων στροφών:
με την ακολουθία των επόμενων στροφών:
 και γωνίας
και γωνίας  κατά την αρνητική φορά (μεταφέρει το
κατά την αρνητική φορά (μεταφέρει το  στο
στο  )
) και γωνίας
και γωνίας  κατά τη θετική φορά (μεταφέρει το
κατά τη θετική φορά (μεταφέρει το  στο
στο 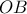 )
) και γωνίας
και γωνίας  κατά την αρνητική φορά (μεταφέρει το
κατά την αρνητική φορά (μεταφέρει το 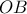 στο
στο  ).
). , έχουμε μεταφορά, οπότε
, έχουμε μεταφορά, οπότε  .
. είναι η άλλη τομή των κύκλων
είναι η άλλη τομή των κύκλων 
 είναι κάθετες στην ευθεία
είναι κάθετες στην ευθεία  .
. στο σχήμα κάθετη στην
στο σχήμα κάθετη στην  , που τέμνει τον "μικρό" μπλε κύκλο στα σημεία
, που τέμνει τον "μικρό" μπλε κύκλο στα σημεία  , οπότε λόγω συμμετριών παίρνουμε:
, οπότε λόγω συμμετριών παίρνουμε: 

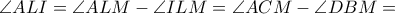


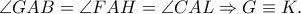
 και
και  οι τομές των μεσοκαθέτων των
οι τομές των μεσοκαθέτων των  με τις
με τις  αντίστοιχα.
αντίστοιχα. είναι κορυφή ισοσκελούς τριγώνου
είναι κορυφή ισοσκελούς τριγώνου  με
με  , καθώς οι
, καθώς οι  σχηματίζουν γωνία ίση με τη γωνία στροφής των ίσων τριγώνων
σχηματίζουν γωνία ίση με τη γωνία στροφής των ίσων τριγώνων  , δηλαδή τη
, δηλαδή τη  .
. .
. .
. είναι το μέσο της
είναι το μέσο της  , το τρίγωνο
, το τρίγωνο  είναι ορθογώνιο, όμοιο με το
είναι ορθογώνιο, όμοιο με το  , καθώς
, καθώς  και
και  , σύμφωνα με το παρακάτω [*]λήμμα[/u][/b] .
, σύμφωνα με το παρακάτω [*]λήμμα[/u][/b] .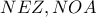 είναι όμοια, με ορθογώνιο μετασχηματισμό ομοιότητας, καθώς έχουν δύο ομόλογες πλευρές κάθετες. Έτσι,
είναι όμοια, με ορθογώνιο μετασχηματισμό ομοιότητας, καθώς έχουν δύο ομόλογες πλευρές κάθετες. Έτσι, 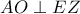
 τριγώνου
τριγώνου  και εξωτερικά αυτού, κατασκευάζουμε ισοσκελή τρίγωνα
και εξωτερικά αυτού, κατασκευάζουμε ισοσκελή τρίγωνα  με άθροισμα γωνιών κορυφής ίσο με
με άθροισμα γωνιών κορυφής ίσο με  . Τότε, το τρίγωνο
. Τότε, το τρίγωνο  έχει γωνίες ίσες με τα μισά των αντιστοίχων γωνιών κορυφής των ισοσκελών τριγώνων. Δηλαδή
έχει γωνίες ίσες με τα μισά των αντιστοίχων γωνιών κορυφής των ισοσκελών τριγώνων. Δηλαδή 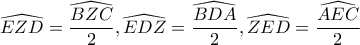 . Το λήμμα εξακολουθεί να ισχύει και στην περίπτωση που κάποιο από τα ισοσκελή τρίγωνα εκφυλιστεί σε ευθύγραμμο τμήμα, δηλαδή κάποια από τις γωνίες κορυφής
. Το λήμμα εξακολουθεί να ισχύει και στην περίπτωση που κάποιο από τα ισοσκελή τρίγωνα εκφυλιστεί σε ευθύγραμμο τμήμα, δηλαδή κάποια από τις γωνίες κορυφής  των ισοσκελών τριγώνων, γίνει ευθεία γωνία, οπότε η αντίστοιχη κορυφή είναι μέσο της πλευράς του
των ισοσκελών τριγώνων, γίνει ευθεία γωνία, οπότε η αντίστοιχη κορυφή είναι μέσο της πλευράς του  . Το λήμμα επίσης ισχύει και στην περίπτωση που κάποιο από τα ισοσκελή τρίγωνα, κατασκευαστεί στο εσωτερικό του
. Το λήμμα επίσης ισχύει και στην περίπτωση που κάποιο από τα ισοσκελή τρίγωνα, κατασκευαστεί στο εσωτερικό του  . Τότε στο άθροισμα θεωρούμε τη μη κυρτή γωνία της κορυφής.
. Τότε στο άθροισμα θεωρούμε τη μη κυρτή γωνία της κορυφής. έχει
έχει  .
. περί το
περί το  κατά γωνία ίση με
κατά γωνία ίση με  , ώστε τη πλευρά
, ώστε τη πλευρά  να συμπέσει με την
να συμπέσει με την  . Τότε εύκολα προκύπτει ότι και το
. Τότε εύκολα προκύπτει ότι και το  είναι ίσο με το
είναι ίσο με το 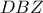 , όπου
, όπου  είναι η εικόνα του
είναι η εικόνα του  , καθώς
, καθώς  και
και  .
. και
και  .
. εγγράψιμα (εύκολο π.χ. από ισότητα
εγγράψιμα (εύκολο π.χ. από ισότητα  ). Τώρα αν θεωρήσω το
). Τώρα αν θεωρήσω το  ως σημειακό κύκλο, αρκεί να δείξω ότι η διαφορά της δύναμης σημείου των
ως σημειακό κύκλο, αρκεί να δείξω ότι η διαφορά της δύναμης σημείου των  ως προς του κύκλους
ως προς του κύκλους  και
και  είναι η ίδια για τα 2 σημεία.
είναι η ίδια για τα 2 σημεία.  . Εστω τώρα ότι οι
. Εστω τώρα ότι οι  τέμνουν τους κύκλους
τέμνουν τους κύκλους  ξανά στα
ξανά στα  αντίστοιχα.
αντίστοιχα. εγγράψιμο αφού
εγγράψιμο αφού  .
. .
. 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες