στην φετινή Μαθηματική Εβδομάδα:
Έστω τρίγωνο
 και η
και η  είναι διχοτόμος. Έστω τυχόν σημείο
είναι διχοτόμος. Έστω τυχόν σημείο  και
και  .
.Να εξεταστεί η ισχύς της συνεπαγωγής:
 ισοσκελές.
ισοσκελές.Συντονιστές: cretanman, Demetres, polysot, socrates, silouan, rek2
 και η
και η  είναι διχοτόμος. Έστω τυχόν σημείο
είναι διχοτόμος. Έστω τυχόν σημείο  και
και  .
. ισοσκελές.
ισοσκελές.Καλησπέρα,Grigoris K. έγραψε:Διατυπώθηκε προφορικά από τον κ. Τσίντσιφα μετά το τέλος της ομιλίας του κ. Βαρβεράκη για το Θ. Steiner-Lehmus
στην φετινή Μαθηματική Εβδομάδα:
Έστω τρίγωνοκαι η
είναι διχοτόμος. Έστω τυχόν σημείο
και
.
Να εξεταστεί η ισχύς της συνεπαγωγής:ισοσκελές.
 με
με  και πάρουμε ως
και πάρουμε ως 
 με τις εξωτερικές διχοτόμους στα
με τις εξωτερικές διχοτόμους στα  τότε σχετικά εύκολα μπορεί να αποδειχθεί οτι
τότε σχετικά εύκολα μπορεί να αποδειχθεί οτι  αλλά προφανώς το
αλλά προφανώς το 
Εκ παραδρομής θεώρησα τοAl.Koutsouridis έγραψε:Καλησπέρα,Grigoris K. έγραψε:Διατυπώθηκε προφορικά από τον κ. Τσίντσιφα μετά το τέλος της ομιλίας του κ. Βαρβεράκη για το Θ. Steiner-Lehmus
στην φετινή Μαθηματική Εβδομάδα:
Έστω τρίγωνοκαι η
είναι διχοτόμος. Έστω τυχόν σημείο
και
.
Να εξεταστεί η ισχύς της συνεπαγωγής:ισοσκελές.
Στην γενική του περίπτωση ο ισχυρισμός δεν ισχύει. Για παράδειγμα αν θεωρήσουμε το τρίγωνομε
και πάρουμε ως
το σημείο τομής της διχοτόμουμε τις εξωτερικές διχοτόμους στα
τότε σχετικά εύκολα μπορεί να αποδειχθεί οτι
αλλά προφανώς το

δεν είναι ισοσκελές.
Στο παραπάνω τρίγωνο έτυχε να πέσω κοιτώντας ένα αρθρο στο πρώτο τεύχος του Kvant 2013, όπου το τρίγωνο αυτό δίνεται ως αντιπαράδειγμα ότι αν οι εξωτερικές διχοτόμοι είναι ίσες σε ενα τρίγωνο και μία απο τις εξωτερικές γωνίες είναι οξεία τότε το τρίγωνο δεν είναι απαραίτητα ισοσκελές, όπως ισχύει στην περίπτωση που οι εξωτερικές γωνίες είναι και οι δύο αμβλείες.
 γενικά σημείο της διχοτόμου
γενικά σημείο της διχοτόμου  αλλά ύστερα απο την υπόδειξη του Grigoris K. ο παραπάνω ισχυρισμός είναι λανθασμένος αφού
αλλά ύστερα απο την υπόδειξη του Grigoris K. ο παραπάνω ισχυρισμός είναι λανθασμένος αφού  εσωτερικό σημείο της
εσωτερικό σημείο της  .
. προκύπτει η ισότητα
προκύπτει η ισότητα

 (βλέπε παρακάτω) και άμεσα (ισότητα τριγώνων
(βλέπε παρακάτω) και άμεσα (ισότητα τριγώνων  και
και  ) η ζητούμενη
) η ζητούμενη  .
. είναι γνησίως αύξουσα για
είναι γνησίως αύξουσα για  , κάτι που προκύπτει από την ανισότητα
, κάτι που προκύπτει από την ανισότητα 
 (για
(για  ).
). ή/και
ή/και  : αυτό δεν ισχύει, καθώς αν για παράδειγμα το
: αυτό δεν ισχύει, καθώς αν για παράδειγμα το  είναι ανάμεσα στα
είναι ανάμεσα στα  (αντί να είναι το
(αντί να είναι το  ανάμεσα στα
ανάμεσα στα  , όπως στο συνημμένο) τότε αντί της
, όπως στο συνημμένο) τότε αντί της  χρησιμοποιείται η
χρησιμοποιείται η  , οπότε
, οπότε  , κλπ]
, κλπ] , τότε ισχύει και
, τότε ισχύει και  για κάθε θέση του σημείου
για κάθε θέση του σημείου  επί της διχοτόμου
επί της διχοτόμου  του
του  και άρα, η συνεπαγωγή της εκφώνησης έπεται.
και άρα, η συνεπαγωγή της εκφώνησης έπεται.
 Έστω ότι ισχύει
Έστω ότι ισχύει  και ας είναι
και ας είναι  το σημείο μεταξύ των
το σημείο μεταξύ των  ώστε
ώστε 
 όπου
όπου  και έστω
και έστω  το συμμετρικό σημείο του
το συμμετρικό σημείο του  ως προς την ευθεία
ως προς την ευθεία  , μεταξύ των
, μεταξύ των  γιατί το
γιατί το  κείται μεταξύ των
κείται μεταξύ των  λόγω
λόγω 


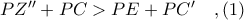




 και το ισοδύναμο ζητούμενο έχει αποδειχθεί.
και το ισοδύναμο ζητούμενο έχει αποδειχθεί. κάτω από την
κάτω από την  .
.Και η απλή απόδειξη : εδώAl.Koutsouridis έγραψε:Καλησπέρα,Grigoris K. έγραψε:Διατυπώθηκε προφορικά από τον κ. Τσίντσιφα μετά το τέλος της ομιλίας του κ. Βαρβεράκη για το Θ. Steiner-Lehmus
στην φετινή Μαθηματική Εβδομάδα:
Έστω τρίγωνοκαι η
είναι διχοτόμος. Έστω τυχόν σημείο
και
.
Να εξεταστεί η ισχύς της συνεπαγωγής:ισοσκελές.
Στην γενική του περίπτωση ο ισχυρισμός δεν ισχύει. Για παράδειγμα αν θεωρήσουμε το τρίγωνομε
και πάρουμε ως
το σημείο τομής της διχοτόμουμε τις εξωτερικές διχοτόμους στα
τότε σχετικά εύκολα μπορεί να αποδειχθεί οτι
αλλά προφανώς το

δεν είναι ισοσκελές.
Στο παραπάνω τρίγωνο έτυχε να πέσω κοιτώντας ένα αρθρο στο πρώτο τεύχος του Kvant 2013, όπου το τρίγωνο αυτό δίνεται ως αντιπαράδειγμα ότι αν οι εξωτερικές διχοτόμοι είναι ίσες σε ενα τρίγωνο και μία απο τις εξωτερικές γωνίες είναι οξεία τότε το τρίγωνο δεν είναι απαραίτητα ισοσκελές, όπως ισχύει στην περίπτωση που οι εξωτερικές γωνίες είναι και οι δύο αμβλείες.
 προκύπτουν οι
προκύπτουν οι
 και η ιδιότητα της διχοτόμου για το
και η ιδιότητα της διχοτόμου για το  οδηγούν στο σύστημα
οδηγούν στο σύστημα![[(b+p)^2+q^2][a(c-p)+bq]^2=[(c-p)^2+q^2][a(b+p)+cq]^2 [(b+p)^2+q^2][a(c-p)+bq]^2=[(c-p)^2+q^2][a(b+p)+cq]^2](/forum/ext/geomar/texintegr/latexrender/pictures/8bea937c94c5d97c6bb8ae2db236d2ac.png)
![(a^2+b^2)[a(c-p)-cq]^2=(a^2+c^2)[a(b+p)-bq]^2. (a^2+b^2)[a(c-p)-cq]^2=(a^2+c^2)[a(b+p)-bq]^2.](/forum/ext/geomar/texintegr/latexrender/pictures/bf99350c645be77477571d1951ad56cc.png)
 και
και  ... αλλά δεν είμαι σε θέση να το αποδείξω αυτό (αλγεβρικά)!
... αλλά δεν είμαι σε θέση να το αποδείξω αυτό (αλγεβρικά)!Το Λήμμα αυτό βέβαια, ούτε προφανές είναι ούτε ευρέως γνωστό και προέκυψε για τις ανάγκες της απόδειξης και θα πρέπει επομένως, για την πληρότητα της λύσης, να παρατεθεί και η απόδειξή του.gbaloglou έγραψε: Μόνη γεωμετρική απόδειξη (προς το παρόν) αυτή του Κώστα (με χρήση του ανισοτικού λήμματος των ισογωνίων).
 και έστω
και έστω  σημεία επί της πλευράς του
σημεία επί της πλευράς του  ώστε να είναι
ώστε να είναι  όπου το
όπου το  μεταξύ των
μεταξύ των  Αποδείξτε ότι
Αποδείξτε ότι 
 ,ισχύει ότι
,ισχύει ότι .
.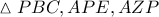 γίνεται
γίνεται 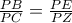 ,δηλαδή
,δηλαδή  .
. έχουμε
έχουμε  .
. !
!Μία ακόμη περίπτωση στο συνημμένο, χωρίς συνέπειες ευτυχώς:gbaloglou έγραψε:[Φαίνεται προς στιγμήν ότι η παραπάνω απόδειξη εξαρτάται από τις σχετικές θέσεις τωνή/και
: αυτό δεν ισχύει, καθώς αν για παράδειγμα το
είναι ανάμεσα στα
(αντί να είναι το
ανάμεσα στα
, όπως στο συνημμένο) τότε αντί της
χρησιμοποιείται η
, οπότε
, κλπ]
 ,
,  κλπ
κλπΕάν η προβολή έστωvittasko έγραψε:ΛΗΜΜΑ. - Δίνεται τρίγωνοκαι έστω
σημεία επί της πλευράς του
ώστε να είναι
όπου το
μεταξύ των
Αποδείξτε ότι
 του
του  επί της
επί της  κείται μεταξύ των
κείται μεταξύ των  το ζητούμενο είναι προφανές αφού ισχύει
το ζητούμενο είναι προφανές αφού ισχύει  και
και 
 , οπότε ισχύει
, οπότε ισχύει 
 Γράφουμε τον κύκλο έστω
Γράφουμε τον κύκλο έστω  με κέντρο το
με κέντρο το  και ακτίνα
και ακτίνα  ο οποίος τέμνει τις
ο οποίος τέμνει τις  τα σημεία έστω
τα σημεία έστω  αντιστοίχως, ως εσωτερικά σημεία των
αντιστοίχως, ως εσωτερικά σημεία των  λόγω της
λόγω της  .
.  με κέντρο το
με κέντρο το  και ακτίνα
και ακτίνα  τέμνει την
τέμνει την  στο σημείο
στο σημείο  μεταξύ των
μεταξύ των  γιατί
γιατί 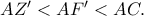
 με κέντρο το
με κέντρο το  και ακτίνα
και ακτίνα  τέμνει την
τέμνει την  στο σημείο
στο σημείο  μεταξύ των
μεταξύ των  γιατί
γιατί 
 και
και  και
και  και
και 
 , να αποδειχθεί ότι ισχύει
, να αποδειχθεί ότι ισχύει 
 Από το
Από το  φέρνουμε παράλληλη ευθεία προς την
φέρνουμε παράλληλη ευθεία προς την  η οποία τέμνει την
η οποία τέμνει την  στο σημείο έστω
στο σημείο έστω  μεταξύ των
μεταξύ των 
 έχουμε
έχουμε  και άρα ισχύει
και άρα ισχύει 


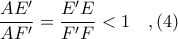


 και το Λήμμα έχει αποδειχθεί.
και το Λήμμα έχει αποδειχθεί.Κώστα με βάση αυτήν την απλή παρατήρηση (που επεκτείνω γωνιακώς στηνvittasko έγραψε:Κι' όμως όλα είναι εφικτά. Για πρώτη φορά δημοσίευση από το χωριό ( όπου δεν υπάρχει ούτε καφενείο ).
Εάν η προβολή έστωvittasko έγραψε:ΛΗΜΜΑ. - Δίνεται τρίγωνοκαι έστω
σημεία επί της πλευράς του
ώστε να είναι
όπου το
μεταξύ των
Αποδείξτε ότι
του
επί της
κείται μεταξύ των
το ζητούμενο είναι προφανές αφού ισχύει
και
Θα εξετάσουμε την περίπτωση όταν το τρίγωνο είναι ορθογώνιο ή αμβλυγώνιο και έστω, οπότε ισχύει
 ) προτείνω την απόδειξη του συνημμένου (όπου
) προτείνω την απόδειξη του συνημμένου (όπου 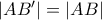 ,
,  , άρα και
, άρα και  λόγω
λόγω  ,
,  με
με  μεταξύ
μεταξύ 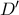 και
και  λόγω
λόγω  , και συνεπώς
, και συνεπώς  ). Πράγματι
). Πράγματι

 , ισοδύναμη προς την
, ισοδύναμη προς την  , που ισχύει λόγω
, που ισχύει λόγω  και
και  (
( αμβλυγώνιο στο
αμβλυγώνιο στο  ).]
).]Νομίζω ότι τελικά η κρίσιμη συνθήκη δεν είναι ηvittasko έγραψε:Κι' όμως όλα είναι εφικτά. Για πρώτη φορά δημοσίευση από το χωριό ( όπου δεν υπάρχει ούτε καφενείο ).
Εάν η προβολή έστωvittasko έγραψε:ΛΗΜΜΑ. - Δίνεται τρίγωνοκαι έστω
σημεία επί της πλευράς του
ώστε να είναι
όπου το
μεταξύ των
Αποδείξτε ότι
του
επί της
κείται μεταξύ των
το ζητούμενο είναι προφανές αφού ισχύει
και
Θα εξετάσουμε την περίπτωση όταν το τρίγωνο είναι ορθογώνιο ή αμβλυγώνιο και έστω, οπότε ισχύει
 αλλά η
αλλά η  (η οποία επίσης οδηγεί στην
(η οποία επίσης οδηγεί στην  , βλέπε και συνημμένο). Στην περίπτωση αυτή η παραπάνω απόδειξη μου εξακολουθεί να ισχύει καθώς από την
, βλέπε και συνημμένο). Στην περίπτωση αυτή η παραπάνω απόδειξη μου εξακολουθεί να ισχύει καθώς από την  έχουμε
έχουμε  και, καίρια,
και, καίρια,  .
. τότε, όπως ήδη επεσήμανε ο Κώστας, ισχύει η
τότε, όπως ήδη επεσήμανε ο Κώστας, ισχύει η  και όλα απλοποιούνται.}
και όλα απλοποιούνται.}Al.Koutsouridis έγραψε: ↑Παρ Απρ 11, 2014 12:24 amΚαλησπέρα,Grigoris K. έγραψε:Διατυπώθηκε προφορικά από τον κ. Τσίντσιφα μετά το τέλος της ομιλίας του κ. Βαρβεράκη για το Θ. Steiner-Lehmus
στην φετινή Μαθηματική Εβδομάδα:
Έστω τρίγωνοκαι η
είναι διχοτόμος. Έστω τυχόν σημείο
και
.
Να εξεταστεί η ισχύς της συνεπαγωγής:ισοσκελές.
Στην γενική του περίπτωση ο ισχυρισμός δεν ισχύει. Για παράδειγμα αν θεωρήσουμε το τρίγωνομε
και πάρουμε ως
το σημείο τομής της διχοτόμουμε τις εξωτερικές διχοτόμους στα
τότε σχετικά εύκολα μπορεί να αποδειχθεί οτι
αλλά προφανώς το

δεν είναι ισοσκελές.
Στο παραπάνω τρίγωνο έτυχε να πέσω κοιτώντας ένα αρθρο στο πρώτο τεύχος του Kvant 2013, όπου το τρίγωνο αυτό δίνεται ως αντιπαράδειγμα ότι αν οι εξωτερικές διχοτόμοι είναι ίσες σε ενα τρίγωνο και μία απο τις εξωτερικές γωνίες είναι οξεία τότε το τρίγωνο δεν είναι απαραίτητα ισοσκελές, όπως ισχύει στην περίπτωση που οι εξωτερικές γωνίες είναι και οι δύο αμβλείες.
 τρίγωνο με δύο ίσες εξωτερικές διχοτόμους σχετίζεται με την ισοσεβιανή κλπ που μελετήσαμε εδώ. Στην παρούσα δημοσίευση υποδεικνύω πως η ισοσεβιανή μπορεί να χρησιμοποιηθεί για την εύρεση και άλλων μη ισοσκελών τριγώνων με δύο ίσες εξωτερικές διχοτόμους, και δίνω ένα 'προσεγγιστικό' τέτοιο τρίγωνο με γωνίες περίπου
τρίγωνο με δύο ίσες εξωτερικές διχοτόμους σχετίζεται με την ισοσεβιανή κλπ που μελετήσαμε εδώ. Στην παρούσα δημοσίευση υποδεικνύω πως η ισοσεβιανή μπορεί να χρησιμοποιηθεί για την εύρεση και άλλων μη ισοσκελών τριγώνων με δύο ίσες εξωτερικές διχοτόμους, και δίνω ένα 'προσεγγιστικό' τέτοιο τρίγωνο με γωνίες περίπου  .
. από το οποίο θέλουμε KAI να περνάει η ισοσεβιανή KAI να είναι το παράκεντρο που αντιστοιχεί στην 'αναζητούμενη' κορυφή
από το οποίο θέλουμε KAI να περνάει η ισοσεβιανή KAI να είναι το παράκεντρο που αντιστοιχεί στην 'αναζητούμενη' κορυφή  . Βρίσκοντας τις εξισώσεις των
. Βρίσκοντας τις εξισώσεις των  ,
,  , όπου
, όπου  ,
,  (δηλαδή
(δηλαδή  ), και εξισώνοντας τις αποστάσεις του
), και εξισώνοντας τις αποστάσεις του  από τις τρεις πλευρές καταλήγουμε στις 'εξισώσεις παρακέντρου'
από τις τρεις πλευρές καταλήγουμε στις 'εξισώσεις παρακέντρου' και
και 
 και λύνοντας (ως προς
και λύνοντας (ως προς  ,
,  ) το σύστημα που αποτελείται (για 'τυχούσα' συγκεκριμένη τιμή του
) το σύστημα που αποτελείται (για 'τυχούσα' συγκεκριμένη τιμή του  ) από την ισοσεβιανή και την πρώτη εξίσωση, καταλήγουμε σε τρίγωνο με παράκεντρο
) από την ισοσεβιανή και την πρώτη εξίσωση, καταλήγουμε σε τρίγωνο με παράκεντρο  επί της ισοσεβιανής (και σε ισότητα επομένως των δύο εξωτερικών διχοτόμων
επί της ισοσεβιανής (και σε ισότητα επομένως των δύο εξωτερικών διχοτόμων  ,
,  ). Αρχίζοντας για παράδειγμα με
). Αρχίζοντας για παράδειγμα με  καταλήγουμε στις τιμές
καταλήγουμε στις τιμές  ,
,  ,
,  ... και στο τρίγωνο που βλέπετε στο συνημμένο. (Η επίλυση του συστήματος 'προσεγγιστικά' λόγω περιορισμένων δυνατοτήτων του WolframAlpha
... και στο τρίγωνο που βλέπετε στο συνημμένο. (Η επίλυση του συστήματος 'προσεγγιστικά' λόγω περιορισμένων δυνατοτήτων του WolframAlpha Πράγματι ... υπάρχει κάτι καλύτερο, που δίνει τις ακριβέστερες τιμές (για το τρίγωνο της προπροηγούμενης δημοσίευσης)gbaloglou έγραψε: ↑Τετ Μάιος 16, 2018 11:54 amΣτο συνημμένο φαίνεται ο αγωνιώδης τρόπος με τον οποίο επιλύθηκε το μη γραμμικό σύστημα που δίνει το παράδειγμα της προηγούμενης δημοσίευσης: είπαμε, δεν μπορούσε να το λύσει το WolframAlpha, οπότε βρήκα την τομή των δύο γραφημάτων με το μάτι και στο περίπου... (Έχω πάντως λόγους να αισιοδοξώ για κάτι καλύτερο!)
 ,
,  (ξεκινώντας από
(ξεκινώντας από  και
και  ).
). και
και 
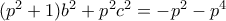

 στην πρώτη εξίσωση -- στην δευτεροβάθμια
στην πρώτη εξίσωση -- στην δευτεροβάθμια 
 , στις 'ρητές' λύσεις
, στις 'ρητές' λύσεις
 ,
,  στην ισοσεβιανή
στην ισοσεβιανή  λαμβάνουμε την 'καμπύλη παρακέντρων'
λαμβάνουμε την 'καμπύλη παρακέντρων'
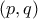 που αντιστοιχούν -- σύμφωνα με όσα παρατέθηκαν σε προηγούμενες δημοσιεύσεις -- σε τρίγωνα κορυφών
που αντιστοιχούν -- σύμφωνα με όσα παρατέθηκαν σε προηγούμενες δημοσιεύσεις -- σε τρίγωνα κορυφών  με δύο ίσες εξωτερικές διχοτόμους. Υποθέτοντας εύλογα
με δύο ίσες εξωτερικές διχοτόμους. Υποθέτοντας εύλογα  ,
,  ,
,  ... καταλήγουμε στον περιορισμό
... καταλήγουμε στον περιορισμό 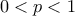 (με ισόπλευρο τρίγωνο για
(με ισόπλευρο τρίγωνο για  και εκφυλισμένο τρίγωνο για
και εκφυλισμένο τρίγωνο για  ). Στο συνημμένο εικονίζεται ολόκληρη η συμμετρικότατη αυτή καμπύλη των παρακέντρων, όπως και η ισοσεβιανή που αντιστοιχεί στο 'διάσημο' τρίγωνο
). Στο συνημμένο εικονίζεται ολόκληρη η συμμετρικότατη αυτή καμπύλη των παρακέντρων, όπως και η ισοσεβιανή που αντιστοιχεί στο 'διάσημο' τρίγωνο  (και στις κορυφές
(και στις κορυφές  ): από τις πέντε 'μη τετριμμένες' τομές των δύο καμπύλων που εικονίζονται μόνη 'αποδεκτή' είναι η
): από τις πέντε 'μη τετριμμένες' τομές των δύο καμπύλων που εικονίζονται μόνη 'αποδεκτή' είναι η  ... που πράγματι οδηγεί, μέσω των παραπάνω 'παραμετρικών' εξισώσεων για τα
... που πράγματι οδηγεί, μέσω των παραπάνω 'παραμετρικών' εξισώσεων για τα  ,
,  , στην τρίτη κορυφή
, στην τρίτη κορυφή  .
.Καλημέρα.Grigoris K. έγραψε: ↑Πέμ Απρ 10, 2014 11:05 pmΔιατυπώθηκε προφορικά από τον κ. Τσίντσιφα μετά το τέλος της ομιλίας του κ. Βαρβεράκη για το Θ. Steiner-Lehmus
στην φετινή Μαθηματική Εβδομάδα:
Έστω τρίγωνοκαι η
είναι διχοτόμος. Έστω τυχόν σημείο
και
.
Να εξεταστεί η ισχύς της συνεπαγωγής:ισοσκελές.
 , αν και μόνο αν οι κύκλοι
, αν και μόνο αν οι κύκλοι  είναι ίσοι, αφού η γωνία
είναι ίσοι, αφού η γωνία  είναι κοινή. Τότε άμεσα παίρνουμε
είναι κοινή. Τότε άμεσα παίρνουμε  Στο περιβάλλον αυτό και αν
Στο περιβάλλον αυτό και αν  έχουμε με βάση το σχήμα που ακολουθεί,
έχουμε με βάση το σχήμα που ακολουθεί,  Επίσης έχουμε
Επίσης έχουμε  Αφαιρούμε τις
Αφαιρούμε τις  κατά μέλη και έτσι προκύπτει
κατά μέλη και έτσι προκύπτει  ή
ή  ή
ή  πράγμα άτοπο, άρα τελικά
πράγμα άτοπο, άρα τελικά 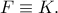 Τότε
Τότε  οπότε άμεσα έχουμε
οπότε άμεσα έχουμε  με
με  Αν
Αν  . Aν
. Aν  τότε και πάλι
τότε και πάλι 
 σημείο επί της διχοτόμου και εντός του τριγώνου τέτοιο ώστε να είναι ίσες οι σεβιανές
σημείο επί της διχοτόμου και εντός του τριγώνου τέτοιο ώστε να είναι ίσες οι σεβιανές  ,
,  . Προεκτείνουμε την
. Προεκτείνουμε την  ως το
ως το  έτσι ώστε να είναι ισοσκελές το
έτσι ώστε να είναι ισοσκελές το  , και έστω
, και έστω  το σημείο τομής της
το σημείο τομής της  με την
με την  . Επειδή η
. Επειδή η  είναι πλέον και ύψος και διάμεσος του ισοσκελούς
είναι πλέον και ύψος και διάμεσος του ισοσκελούς  , προκύπτει εύκολα από ισότητες τριγώνων η ισότητα
, προκύπτει εύκολα από ισότητες τριγώνων η ισότητα  |. Είναι δηλαδή ίσα τα μήκη των
|. Είναι δηλαδή ίσα τα μήκη των  ,
,  ,
,  , παρά το ότι συντρέχουν στο
, παρά το ότι συντρέχουν στο  (και έχουν και τα τρία τα άκρα τους επί των ημιευθειών
(και έχουν και τα τρία τα άκρα τους επί των ημιευθειών  ,
,  ): αυτό είναι αδύνατον, σύμφωνα (και) με την παρακάτω αλγεβρική θεώρηση.
): αυτό είναι αδύνατον, σύμφωνα (και) με την παρακάτω αλγεβρική θεώρηση. ,
,  ,
, 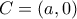 ,
,  -- όπου
-- όπου  τυχόν σημείο εντός ή εκτός του τριγώνου
τυχόν σημείο εντός ή εκτός του τριγώνου  -- αναζητούμε σημεία
-- αναζητούμε σημεία 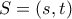 και
και 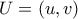 επί των ευθειών των
επί των ευθειών των  ,
,  αντίστοιχα τέτοια ώστε η μεταξύ τους απόσταση να είναι ίση προς 'δοθέντα' αριθμό
αντίστοιχα τέτοια ώστε η μεταξύ τους απόσταση να είναι ίση προς 'δοθέντα' αριθμό  και να είναι συνευθειακά με το
και να είναι συνευθειακά με το  . Επειδή το
. Επειδή το 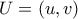 είναι η τομή των
είναι η τομή των  ,
,  , οι συντεταγμένες
, οι συντεταγμένες  ,
,  μπορούν να εκφρασθούν συναρτήσει των
μπορούν να εκφρασθούν συναρτήσει των  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , και η συνθήκη
, και η συνθήκη  να γραφεί ως
να γραφεί ως ![[(a-b)pt+cp(s-a)+(b-a)st+(a-s)cs}]^2+[(a-s)ct+cq(s-a)+(b-a)t^2+(a-b)qt]^2= [(a-b)pt+cp(s-a)+(b-a)st+(a-s)cs}]^2+[(a-s)ct+cq(s-a)+(b-a)t^2+(a-b)qt]^2=](/forum/ext/geomar/texintegr/latexrender/pictures/bb1fa298f4e4c9fda1def9455050b708.png)
![=d^2[(a-b)t+(b-a)q+c(s-p)]^2. =d^2[(a-b)t+(b-a)q+c(s-p)]^2.](/forum/ext/geomar/texintegr/latexrender/pictures/735394627b88ae650c8ac4628748420a.png)
 ώστε να προσδιορισθούν οι δυνατές θέσεις του
ώστε να προσδιορισθούν οι δυνατές θέσεις του 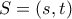 επί της
επί της  . Αντικαθιστώντας γραμμικά το
. Αντικαθιστώντας γραμμικά το  συναρτήσει του
συναρτήσει του  στην κογχοειδή λαμβάνουμε μία εξίσωση τετάρτου βαθμού ως προς
στην κογχοειδή λαμβάνουμε μία εξίσωση τετάρτου βαθμού ως προς  , που φυσικά δεν μπορεί να έχει περισσότερες από
, που φυσικά δεν μπορεί να έχει περισσότερες από  πραγματικές ρίζες.
πραγματικές ρίζες. , κάθε σημείο
, κάθε σημείο  'εντός' της γωνίας, και κάθε
'εντός' της γωνίας, και κάθε 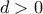 υπάρχουν σημεία
υπάρχουν σημεία  ,
,  επί των προεκτάσεων των ημιευθειών
επί των προεκτάσεων των ημιευθειών  ,
,  , αντίστοιχα, και οι αντίστοιχες τομές
, αντίστοιχα, και οι αντίστοιχες τομές  ,
,  των
των  ,
,  με τις ημιευθείες
με τις ημιευθείες  ,
,  , έτσι ώστε
, έτσι ώστε  . Υπάρχουν δηλαδή ΠΑΝΤΟΤΕ 2 'προεκτασιακές' λύσεις της
. Υπάρχουν δηλαδή ΠΑΝΤΟΤΕ 2 'προεκτασιακές' λύσεις της  , επιτρέποντας μόνον
, επιτρέποντας μόνον  'εσωτερικές' λύσεις. Επειδή υποθέσαμε εξ αρχής ότι το επί της διχοτόμου σημείο
'εσωτερικές' λύσεις. Επειδή υποθέσαμε εξ αρχής ότι το επί της διχοτόμου σημείο  (από το οποίο διέρχονται τα
(από το οποίο διέρχονται τα  ισομήκη τμήματα
ισομήκη τμήματα  ,
,  ,
,  ) βρίσκεται στο εσωτερικό του τριγώνου
) βρίσκεται στο εσωτερικό του τριγώνου  , έχουμε καταλήξει σε άτοπο -- εκτός και αν το
, έχουμε καταλήξει σε άτοπο -- εκτός και αν το  είναι όντως ισοσκελές.
είναι όντως ισοσκελές. επί της διχοτόμου αλλά εκτός του τριγώνου
επί της διχοτόμου αλλά εκτός του τριγώνου  ... με δύο 'προεκτασιακές' (μία από τις οποίες διέρχεται από την κορυφή
... με δύο 'προεκτασιακές' (μία από τις οποίες διέρχεται από την κορυφή  ) και δύο 'έσωτερικές' λύσεις (μία από τις οποίες διέρχεται από την κορυφή
) και δύο 'έσωτερικές' λύσεις (μία από τις οποίες διέρχεται από την κορυφή  ). Το σημείο
). Το σημείο  είναι τομή της διχοτόμου και της ισοσεβιανής που συζητήθηκε εδώ. Σίγουρα πρόκειται για ένα 'εξειδικευμένο' παράδειγμα, που επαληθεύει πάντως τους παραπάνω υπολογισμούς. (Εννοείται ότι η ακρίβεια του σχήματος δεν είναι απόλυτη, αλλά είναι χαρακτηριστικό ότι μία από τις προσεγγιστικές λύσεις,
είναι τομή της διχοτόμου και της ισοσεβιανής που συζητήθηκε εδώ. Σίγουρα πρόκειται για ένα 'εξειδικευμένο' παράδειγμα, που επαληθεύει πάντως τους παραπάνω υπολογισμούς. (Εννοείται ότι η ακρίβεια του σχήματος δεν είναι απόλυτη, αλλά είναι χαρακτηριστικό ότι μία από τις προσεγγιστικές λύσεις,  (αντιστοιχούσα στην κορυφή
(αντιστοιχούσα στην κορυφή  ), πλησιάζει πολύ τον
), πλησιάζει πολύ τον  ) ... και οι πιο δύσπιστοι μπορούν να δουν ότι η προσεγγιστική λύση
) ... και οι πιο δύσπιστοι μπορούν να δουν ότι η προσεγγιστική λύση  οδηγεί -- μέσω των τύπων για τα
οδηγεί -- μέσω των τύπων για τα  ,
,  που δεν παρέθεσα αναλυτικά αλλά προκύπτουν εύκολα από εξισώσεις και τομές ευθειών -- πολύ κοντά στην κορυφή
που δεν παρέθεσα αναλυτικά αλλά προκύπτουν εύκολα από εξισώσεις και τομές ευθειών -- πολύ κοντά στην κορυφή 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες