Μια λύση με συμμετρική αντιστροφή/μετρικές σχέσεις:

- mixtilinear1.png (64.58 KiB) Προβλήθηκε 1407 φορές
Παίρνουμε συμμετρική αντιστροφή κέντρου

που στέλνει το

στο

.
Η

πάει στον

.Έτσι το

πάει στο μέσο του τόξου

,
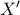
,ενώ το

από γνωστή ισογωνιότητα που αναφέρθηκε παραπάνω,πάει στην προβολή
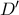
του

παρακέντρου.Έτσι ο

πάει στην ευθεία
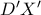
.
To

πάει σε σημείο της

ώστε

δηλαδή στην τομή της

με την εκ του

παράλληλη στη διχοτόμο

.
Ανάλογα ορίζεται και το

.
Αν

οι προβολές των

παρακέντρων στις
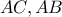
αντίστοιχα,τότε το

πάει στην τομή της

(ανήκει στον

) με την εκ του

παράλληλη στην

,έστω
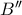
(

από ισογωνιότητες/εγγράψιμα από όπου έπεται η παραλληλία).Έστω

το αντίστοιχο του

.
Έτσι οι

πάνε στους

αντίστοιχα.

- mixtilineaar2.png (56.23 KiB) Προβλήθηκε 1407 φορές
(2ο σχήμα)Θέλουμε να δείξουμε πως η κοινή χορδή των

περνάει από τα

.
Το κάνουμε μετρικά.
Πρώτα για το
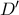
:
Από Θαλή στις

προκύπτει

.
Αρκεί

το οποίο δείχνεται εύκολα με πράξεις.
Έπειτα για το
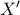
:
Αν

τα κέντρα των
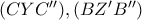
αντίστοιχα δείχνουμε πως

κάθετες και έχουμε τελειώσει.
Αν
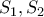
οι προβολές των κέντρων στην

και

εκείνες στη μεσοκάθετο

έχουμε:

κι άρα

.
Λόγω

κτλ. έχουμε πως τα

ανήκουν στις εξωτερικές διχοτόμους των

αντίστοιχα.
Έτσι με

το

παράκεντρο έχουμε τις ομοιότητες

και

από όπου με βάση και τα προηγούμενα παίρνουμε εύκολα

από όπου

.
Από

και
Θεώρημα Κούτρα αρκεί

.
Το

όμως ισούται με

.Επειδή

από τα ορθογώνια

αρκεί τελικά

.
Είναι

όπου

η ακτίνα του εγγεγραμμένου.
Αντικαθιστώντας και κάνοντας τις πράξεις το ζητούμενο είναι άμεσο.
 ένα τρίγωνο με έκκεντρο
ένα τρίγωνο με έκκεντρο  , και έστω
, και έστω  ,
,  ,
,  οι τομές των
οι τομές των  ,
,  ,
,  με τις πλευρές
με τις πλευρές  ,
, 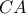 , and
, and  . Θεωρούμε
. Θεωρούμε 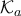 τον κύκλο που εφάπτεται στις πλευρές
τον κύκλο που εφάπτεται στις πλευρές  ,
,  , και εσωτερικά στον περιγεγραμμένο κύκλο
, και εσωτερικά στον περιγεγραμμένο κύκλο  του
του  , και έστω
, και έστω  το σημείο επαφής τους. Όμοια ορίζονται τα
το σημείο επαφής τους. Όμοια ορίζονται τα 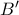 , και
, και  .
.  ,
,  , και
, και  περνούν όλοι από δύο διαφορετικά σημεία.
περνούν όλοι από δύο διαφορετικά σημεία.
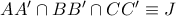 .
. για παράδειγμα, είναι ισογώνια της
για παράδειγμα, είναι ισογώνια της  ως προς την γωνία
ως προς την γωνία  , όπου
, όπου 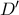 ( δεν εμφανίζεται στο σχήμα ) είναι το σημείο επαφής της πλευράς
( δεν εμφανίζεται στο σχήμα ) είναι το σημείο επαφής της πλευράς  -παρεγγεγραμμένο κύκλο του
-παρεγγεγραμμένο κύκλο του  και ομοίως για τις ευθείες
και ομοίως για τις ευθείες  .
. δηλαδή, είναι το ισογώνιο σημείο του
δηλαδή, είναι το ισογώνιο σημείο του  Εύκολα προκύπτει ότι οι ριζικοί άξονες των κύκλων
Εύκολα προκύπτει ότι οι ριζικοί άξονες των κύκλων  λαμβανομένων ανά δύο, περνάνε από το σημείο
λαμβανομένων ανά δύο, περνάνε από το σημείο 
 και ας είναι το
και ας είναι το  εκτός του
εκτός του  , είναι η κοινή χορδή των κύκλων
, είναι η κοινή χορδή των κύκλων  , προκύπτει εύκολα ότι το τετράπλευρο
, προκύπτει εύκολα ότι το τετράπλευρο  είναι εγγράψιμο και αρκεί να αποδειχθεί ότι ο περίκυκλός του περνάει από το σημείο
είναι εγγράψιμο και αρκεί να αποδειχθεί ότι ο περίκυκλός του περνάει από το σημείο  στο
στο  .
. .Έτσι το
.Έτσι το 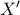 ,ενώ το
,ενώ το  από γνωστή ισογωνιότητα που αναφέρθηκε παραπάνω,πάει στην προβολή
από γνωστή ισογωνιότητα που αναφέρθηκε παραπάνω,πάει στην προβολή  πάει στην ευθεία
πάει στην ευθεία 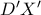 .
. πάει σε σημείο της
πάει σε σημείο της  δηλαδή στην τομή της
δηλαδή στην τομή της  .
. .
. οι προβολές των
οι προβολές των  παρακέντρων στις
παρακέντρων στις 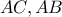 αντίστοιχα,τότε το
αντίστοιχα,τότε το  πάει στην τομή της
πάει στην τομή της  ,έστω
,έστω 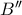 (
( από ισογωνιότητες/εγγράψιμα από όπου έπεται η παραλληλία).Έστω
από ισογωνιότητες/εγγράψιμα από όπου έπεται η παραλληλία).Έστω  το αντίστοιχο του
το αντίστοιχο του  .
. πάνε στους
πάνε στους  αντίστοιχα.
αντίστοιχα.
 .
. προκύπτει
προκύπτει  .
. το οποίο δείχνεται εύκολα με πράξεις.
το οποίο δείχνεται εύκολα με πράξεις. τα κέντρα των
τα κέντρα των 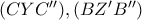 αντίστοιχα δείχνουμε πως
αντίστοιχα δείχνουμε πως  κάθετες και έχουμε τελειώσει.
κάθετες και έχουμε τελειώσει.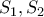 οι προβολές των κέντρων στην
οι προβολές των κέντρων στην  εκείνες στη μεσοκάθετο
εκείνες στη μεσοκάθετο  έχουμε:
έχουμε: κι άρα
κι άρα  .
. κτλ. έχουμε πως τα
κτλ. έχουμε πως τα  το
το  και
και  από όπου με βάση και τα προηγούμενα παίρνουμε εύκολα
από όπου με βάση και τα προηγούμενα παίρνουμε εύκολα  από όπου
από όπου  .
. και Θεώρημα Κούτρα αρκεί
και Θεώρημα Κούτρα αρκεί  .
. όμως ισούται με
όμως ισούται με  .Επειδή
.Επειδή  από τα ορθογώνια
από τα ορθογώνια  αρκεί τελικά
αρκεί τελικά  .
. όπου
όπου  η ακτίνα του εγγεγραμμένου.
η ακτίνα του εγγεγραμμένου.