Δίνεται τρίγωνο
 εγγεγραμμένο σε τρίγωνο
εγγεγραμμένο σε τρίγωνο  (το
(το  βρίσκεται στην
βρίσκεται στην  ,το
,το  βρίσκεται στην
βρίσκεται στην  , το
, το  βρίσκεται στην
βρίσκεται στην  ). Ισχύει ότι
). Ισχύει ότι  .
.Ήθελα να έχω μια ικανή συνθήκη έτσι ώστε τα τρίγωνα
 ,
,  να είναι όμοια. Δεν το έψαξα γιατί δεν είχα χρόνο...
να είναι όμοια. Δεν το έψαξα γιατί δεν είχα χρόνο...Όμως βρήκα αυτό που ήθελα στο βιβλίο '' ΠΑΝΕΝΩΣΙΑΚΕΣ ΜΑΘΗΜΑΤΙΚΕΣ ΟΛΥΜΠΙΑΔΕΣ ΤΗΣ Ε.Σ.Σ.Δ. '' τόμος 2 . Συγκεκριμένα πρόκειται για το θέμα 500 στο βιβλίο αυτό , ένα θέμα που έπεσε στην 23η Πανενωσιακή Ολυμπιάδα που έγινε στη Ρίγα.
Με χαρά σας το προτείνω.
Στις πλευρές
 ,
, και
και  τριγώνου
τριγώνου  βάφτηκαν με πράσινο χρώμα τα σημεία
βάφτηκαν με πράσινο χρώμα τα σημεία 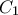 ,
,  και
και  αντίστοιχα , διάφορα από τις κορυφές του τριγώνου.
αντίστοιχα , διάφορα από τις κορυφές του τριγώνου.Εξάλλου , γι' αυτά ισχύει
 και
και 
Αποδείξτε ότι το τρίγωνο με τις πράσινες κορυφές είναι όμοιο με το τρίγωνο

Στο όμορφο αυτό θέμα ας μου επιτραπεί ακόμα ένα ζητούμενο .
Αν
 η κοινή τιμή των λόγων
η κοινή τιμή των λόγων 
βρείτε το λόγο ομοιότητας των ομοίων τριγώνων του προαναφερθέντος θέματος συναρτήσει του


 (
(
 ). Όπως αποδείξαμε εδώ:
). Όπως αποδείξαμε εδώ:  είναι παραλληλόγραμμο, οπότε
είναι παραλληλόγραμμο, οπότε  και επειδή
και επειδή 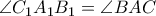 άρα και
άρα και  (κόκκινες γωνίες)
(κόκκινες γωνίες)  είναι εγγράψιμο, οπότε
είναι εγγράψιμο, οπότε  (γαλάζιες γωνίες) και αφού τα δύο τρίγωνο έχουν δύο ίσες γωνίες θα έχουν και τις τρίτες γωνίες ίσες και το πρώτο ζητούμενο εδείχθη.
(γαλάζιες γωνίες) και αφού τα δύο τρίγωνο έχουν δύο ίσες γωνίες θα έχουν και τις τρίτες γωνίες ίσες και το πρώτο ζητούμενο εδείχθη.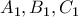 πάνω στις αντίστοιχες πλευρές αλλά δεν νομίζω ότι θα αλλάξει κάτι και κυρίως δεν έχω άλλο ελεύθερο χρόνο για διερεύνηση.)
πάνω στις αντίστοιχες πλευρές αλλά δεν νομίζω ότι θα αλλάξει κάτι και κυρίως δεν έχω άλλο ελεύθερο χρόνο για διερεύνηση.) τότε:
τότε: 
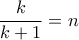 και αν
και αν 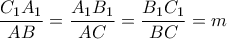 τότε:
τότε:



 με το ίσον του,
με το ίσον του,  , παίρνουμε τον ζητούμενο λόγο ομοιότητας των δύο τριγώνων.
, παίρνουμε τον ζητούμενο λόγο ομοιότητας των δύο τριγώνων. όπου
όπου  με
με 
 και μετά από κάποιες πράξεις καταλήγουμε ότι
και μετά από κάποιες πράξεις καταλήγουμε ότι
 να είναι όμοια ;
να είναι όμοια ;
 και
και  και
και  τότε μάλλον καλά πάνε τα πράγματα...
τότε μάλλον καλά πάνε τα πράγματα... είναι η μικρότερη πλευρά του τριγώνου.
είναι η μικρότερη πλευρά του τριγώνου. έχω ότι
έχω ότι 
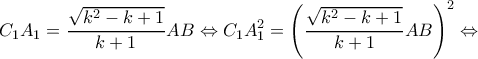




 και αφού
και αφού  ισοδύναμα έχω ότι
ισοδύναμα έχω ότι 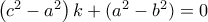 που ισοδυναμεί με
που ισοδυναμεί με 
 έχω ότι
έχω ότι 



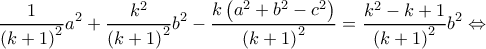
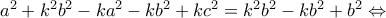
 έχω ότι
έχω ότι 






 και οι λύσεις της είναι το
και οι λύσεις της είναι το  και το
και το 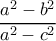
 με μικρότερη πλευρά την
με μικρότερη πλευρά την  εγγεγραμμένο στο τρίγωνο
εγγεγραμμένο στο τρίγωνο  , το
, το  .
. τότε τα τρίγωνα
τότε τα τρίγωνα  είναι όμοια και αντιστρόφως.
είναι όμοια και αντιστρόφως.