Μαθηματικοί Διαγωνισμοί
Χαράλαμπος Στεργίου-Σιλουανός Μπραζιτίκος
άσκηση
Έστω τρίγωνο ΑΒΓ με

Τα σημεία Μ,Ν βρίσκονται στη ΒΓ τέτοια ώστε το Ν να είναι μεταξύ των Μ,Γ.
Αν ισχύει
 , να αποδείξετε ότι
, να αποδείξετε ότι
Συντονιστές: cretanman, Demetres, polysot, socrates, silouan, rek2

 , να αποδείξετε ότι
, να αποδείξετε ότι

 άρα
άρα  , οπότε
, οπότε  .
. ,
,

 , κλπ
, κλπ Δια του σημείου
Δια του σημείου  φέρνουμε την κάθετη ευθεία επί την
φέρνουμε την κάθετη ευθεία επί την  η οποία τέμνει τον κύκλο
η οποία τέμνει τον κύκλο  με κέντρο το
με κέντρο το  και ακτίνα
και ακτίνα  στο σημείο έστω
στο σημείο έστω 
 επί την χορδή
επί την χορδή  του
του  τέμνει την πλευρά
τέμνει την πλευρά  του δοσμένου ορθογωνίου και ισοσκελούς τριγώνου
του δοσμένου ορθογωνίου και ισοσκελούς τριγώνου  στο σημείο έστω
στο σημείο έστω  και θα αποδείξουμε ότι
και θα αποδείξουμε ότι 
 είναι οι μεσοκάθετες των
είναι οι μεσοκάθετες των  αντιστοίχως και έτσι έχουμε ότι
αντιστοίχως και έτσι έχουμε ότι 
 και
και 
 καθώς επίσης και ότι το τριγωνο
καθώς επίσης και ότι το τριγωνο  είναι ορθογώνιο στο σημείο
είναι ορθογώνιο στο σημείο  γιατί
γιατί  .
. Στο ορθογώνιο λοιπόν τρίγωνο
Στο ορθογώνιο λοιπόν τρίγωνο  έχουμε ότι
έχουμε ότι 
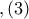



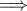

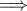
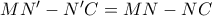


 Είναι εύκολο τώρα να δούμε ότι
Είναι εύκολο τώρα να δούμε ότι  και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. τέτοιες ώστε
τέτοιες ώστε  τέμνουν την ευθεία
τέμνουν την ευθεία  στα σημεία έστω
στα σημεία έστω  αντιστοίχως ( όχι απαραίτητα μεταξύ των
αντιστοίχως ( όχι απαραίτητα μεταξύ των  ), ισχύει πάντοτε η
), ισχύει πάντοτε η 
 το μέσον της
το μέσον της  και το τετράγωνο
και το τετράγωνο  .
.
 ..
..
 :
: 

 που είναι ισοδύναμη με την
που είναι ισοδύναμη με την  συνεπώς ισχύει. Άρα
συνεπώς ισχύει. Άρα  οπότε
οπότε 
 έχουμε αντίστοιχα
έχουμε αντίστοιχα και
και  και
και 
 εύκολα έχουμε
εύκολα έχουμε 



Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης