Δροσερό καφεδάκι

kkoudas · #1

Κάθε μέρα δροσίζω τον καφέ μου με 3 παγάκια, τα οποία παίρνω τυχαία από την 10θέσια παγοθήκη μου, και κατόπιν ξαναγεμίζω με νερό τις άδειες θέσεις, για να έχω μια γεμάτη παγοθήκη και την επόμενη μέρα. Κάθε πόσες μέρες (κατά μέσο όρο) ανανεώνονται όλες οι θήκες με καινούριο νερό;

Λάμπρος Κατσάπας · #2

kkoudas έγραψε: ↑
Σάβ Ιουν 29, 2019 10:36 pm
Κάθε μέρα δροσίζω τον καφέ μου με 3 παγάκια, τα οποία παίρνω τυχαία από την 10θέσια παγοθήκη μου, και κατόπιν ξαναγεμίζω με νερό τις άδειες θέσεις, για να έχω μια γεμάτη παγοθήκη και την επόμενη μέρα. Κάθε πόσες μέρες (κατά μέσο όρο) ανανεώνονται όλες οι θήκες με καινούριο νερό;

Αν με

συμβολίσουμε τον αναμενόμενο χρόνο μέχρι να ανανεωθούν όλα τα παγάκια δεδομένου ότι έχουν ήδη

ανανεωθεί ακριβώς

τότε η ζητούμενη μέση τιμή E_0

μπορεί να προκύψει από τη λύση του παρακάτω

συστήματος (όχι με το χέρι

):

και για

$E_k=1+ \sum_{j=0}^{3}\dfrac{\binom{k}{3-j}\binom{10-k}{j}}{\binom{10}{3}}E_{k+j}$

όπου συμβατικά θεωρούμε $E_{10}=E_{11}=E_{12}=0$ .

Για παράδειγμα για k=4

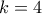έχουμε ότι βρισκόμαστε στην κατάσταση

(δηλαδή έχουν ανανεωθεί

μόνο παγάκια) και με πιθανότητα $\dfrac{\binom{4}{3}}{\binom{10}{3}}$ παραμένουμε σε αυτή την

κατάσταση, με πιθανότητα $\dfrac{\binom{4}{2}\binom{6}{1}}{\binom{10}{3}}$ πάμε σε κατάσταση

, με

πιθανότητα $\dfrac{\binom{4}{1}\binom{6}{2}}{\binom{10}{3}}$ πάμε σε κατάσταση

και τέλος με

πιθανότητα $\dfrac{\binom{4}{0}\binom{6}{3}}{\binom{10}{3}}$ πάμε σε κατάσταση

.

Η λύση του παραπάνω συστήματος δίνει E_0=9.04621.

Παρακάτω βάζω και μια εικόνα όπου φαίνεται η επίλυση του προβλήματος με Monte Carlo simulation στο πακέτο

Mathematica. Υπολογίζεται η προσεγγιστική μέση τιμή, η τυπική απόκλιση και δίνεται στο ιστόγραμμα η προσεγγιστική

κατανομή του χρόνου μέχρι να ανανεωθούν όλα τα παγάκια.

kkoudas · #3

Την ίδια ακριβώς λύση έφτιαξα κι εγώ! Μόνο τα σύμβολα j,k

ήταν διαφορετικά και τα $E_\nu$ ορισμένα ανάποδα (είχα πάρει $E_\nu=$ ημέρες μέχρι να ανανεωθούν όλα, όταν έχουν μείνει $\nu$ παλιά παγάκια)... Τι πιθανότητα έχει αυτό;

Λάμπρος Κατσάπας · #4

kkoudas έγραψε: ↑
Δευ Ιούλ 01, 2019 1:34 am
Τι πιθανότητα έχει αυτό;

Έστω

η τ.μ. που καταμετρεί το πλήθος από διαφορετικά παγάκια που έχουμε μαζέψει μέχρι την χρονική στιγμή

.

Ορίζουμε T=min(n:X_n=10).

H

είναι χρόνος διακοπής (stopping time).

Για την κατανομή της

μπορούμε να δουλέψουμε με τον πίνακα πιθανοτήτων μετάβασης (η X_n

έχει

την ιδιότητα Markov). Οι καταστάσεις είναι οι 0,3,4,...,10

. Ο πίνακας πιθανοτήτων μετάβασης (ενός βήματος) είναι ο

$P=\begin{pmatrix} 0 & 1& 0 & 0& 0& 0 & 0 &0 &0 \\ 0& \frac{\binom{3}{3}\binom{7}{0}}{\binom{10}{3}} & \frac{\binom{3}{2}\binom{7}{1}}{\binom{10}{3}} & \frac{\binom{3}{1}\binom{7}{2}}{\binom{10}{3}}& \frac{\binom{3}{0}\binom{7}{3}}{\binom{10}{3}}& 0 & 0& 0 &0 \\ 0&0 & \frac{\binom{4}{3}\binom{6}{0}}{\binom{10}{3}} &\frac{\binom{4}{2}\binom{6}{1}}{\binom{10}{3}} & \frac{\binom{4}{1}\binom{6}{2}}{\binom{10}{3}} & \frac{\binom{4}{0}\binom{6}{3}}{\binom{10}{3}} &0 & 0&0 \\ 0& 0& 0 & * & * & * &* & 0 &0 \\ 0& 0&0 &0 &* &* & * &* & 0\\ 0& 0 &0 & 0& 0 & *& * & * & *\\ 0& 0 & 0 & 0 &0 & 0 & \frac{\binom{8}{3}\binom{2}{0}}{\binom{10}{3}}& \frac{\binom{8}{2}\binom{2}{1}}{\binom{10}{3}} & \frac{\binom{8}{1}\binom{2}{2}}{\binom{10}{3}}\\ 0& 0 & 0 & 0 & 0 & 0 & 0& \frac{\binom{9}{3}\binom{1}{0}}{\binom{10}{3}}&\frac{\binom{9}{2}\binom{1}{1}}{\binom{10}{3}} \\ 0& 0& 0 & 0 &0 &0 &0 &0 & 1 \end{pmatrix}$

ο οποίος έχει ιδιοτιμές τα διαγώνια στοιχεία (είναι άνω τριγωνικός) και από το φασματικό θεώρημα της Γραμμικής

Άλγεβρας έχουμε ότι γράφεται $P=QLQ^{-1}$ όπου

o πίνακας με τα ιδιοδιανύσματα και

ο

διαγώνιος με στοιχεία της διαγωνίου τις ιδιοτιμές. Άρα $P^k=QL^kQ^{-1},k=1,2,3,...$ . To $a_{1,9}$

στοιχείο του P^k

μας δίνει την πιθανότητα να φτάσουμε από κατάσταση

σε κατάσταση

σε

βήματα. Επειδή στο υπολογισμό αυτής της πιθανότητας συνυπολογίζονται και τα ενδεχόμενα να έχουμε

πιάσει κατάσταση

σε λιγότερα βήματα από

και μετά, στα επόμενα βήματα, να παραμένουμε σε

αυτή την κατάσταση η ζητούμενη κατανομή $P(T=k)=P(X_k=10,X_{k-1}<10)$ για k=4,5,...

θα είναι το στοιχείο $b_{1,9}$ του $QL^kQ^{-1}-QL^{k-1}Q^{-1}$ . Οι υπολογισμοί έγιναν στο mathematica

και έδωσαν τελικά (το όχι και τόσο κομψό)

$P(T=k)=3 \left ( \dfrac{10}{7} \right )^{1 - k} + 85 \left ( \dfrac{24}{7} \right )^{1 - k} + 77 \cdot 3^{2 - k} \cdot 4^{1 - k}$

$- 175 \cdot 6^{1 - k} - 8 \cdot 3^{2 - k} \cdot 5^{1 - k} \cdot 7^{k-1} - 203 \cdot 30^{1 - k} + 119 \cdot 120^{1 - k}$

και το γράφημά της είναι στην παρακάτω εικόνα

Δροσερό καφεδάκι

Δροσερό καφεδάκι

Re: Δροσερό καφεδάκι

Re: Δροσερό καφεδάκι

Re: Δροσερό καφεδάκι

Μέλη σε σύνδεση