Είμαι καινούριος στο υπέροχο forum αυτο, το οποίο βρήκα, αναζητόντας λύση/επεξίγηση σε ένα θέμα εξετάσεων της σχολής μου.
Ψάχνοντας λοιπόν παλαιότερα θέματα (μιάς που πρώτη φορά θα δώσω το μάθημα, έπεσε το μάτι μου σε αυτό το ενδιαφέρον θέμα:
--------------------------------------------------
Στο παρακάτω ολοκλήρωμα, αφού γίνει αλλαγή μεταβλητών
 και
και  , να υπολογιστεί.
, να υπολογιστεί.
--------------------------------------------------
Το ζήτημά μου δεν είναι το πώς λύνεται η άσκηση, αλλα το με ποιόν τρόπο θα φτάσω στο σημέιο να λύσω το 2x2 matrix (καθως, απ ότι έχω καταλάβει, κάπως έτσι πρέπει να λυθεί)... Με λίγα λόγια, έχω κολλήσει και δεν μπορώ να καταλάβω πώς θα έπρεπε να λύσω ως προς x και ως προς y...
Έχει κάποιος καμία ιδέα/hint/πρόταση;
Ευχαριστώ εκ των προτέρων
Ανδρέας Μ.

 , ως προς
, ως προς  ,
,  ;
; 



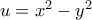 και όχι
και όχι  .
.

 . Παρατηρούμε ότι
. Παρατηρούμε ότι 
 θα απλοποιηθεί με το
θα απλοποιηθεί με το  και έτσι δεν είναι απαραίτητο να την εκφράσουμε ως προς
και έτσι δεν είναι απαραίτητο να την εκφράσουμε ως προς  , ως θα οφείλαμε. Έτσι
, ως θα οφείλαμε. Έτσι 

 από
από  σε
σε  .
. . Παρόμοιο θεώρημα ισχύει και για αλλαγής μεταβλητών στον
. Παρόμοιο θεώρημα ισχύει και για αλλαγής μεταβλητών στον  . Η θεωρία άλλωστε υπάρχει σε κάθε βιβλίο λογισμού πολλών μεταβλητών:
. Η θεωρία άλλωστε υπάρχει σε κάθε βιβλίο λογισμού πολλών μεταβλητών: θέλουμε να υπολογίσουμε το ολοκλήρωμα
θέλουμε να υπολογίσουμε το ολοκλήρωμα  και για κάποιον λόγο θέλουμε να κάνουμε αντικατάσταση των μεταβλητών
και για κάποιον λόγο θέλουμε να κάνουμε αντικατάσταση των μεταβλητών  , με τις μεταβλητές
, με τις μεταβλητές  .
. 
 της
της  :
:  .
. 