Νεγρεπόντης Στυλιανός
Α-1. (α) Δώστε τον ορισμό της βάσης τοπολογίαςκαι τον ορισμό της βάσης περιοχών σε ένα τοπολογικό χώρο
(β) Διατυπώστε και αποδείξτε το κριτήριο Hausdorff ισότητος τοπολογιών
Α-2. (α) Δώστε τον ορισμό της κλειστότητας και του εσωτερικού ενός υποσυνόλου ενός τοπολογικού χώρου.
(β) Έστω Χ τοπολογικός χώρος και
 .
.Αποδείξτε ότι τα εξής είναι ισοδύναμα:
(ι) G είναι ανοικτό
(ιι)

για κάθε
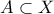
Α-3. (α) Έστω Χ πρώτος αριθμήσιμος τοπολογικός χώρος ,
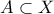 και
και 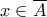
Αποδείξτε ότι υπάρχει ακολουθία
 στο Α ώστε
στο Α ώστε 
(β) Δώστε παράδειγμα με πλήρη απόδειξη , ενός τοπολογικού χώρου στον οποίο δεν ισχύει το συμπέρασμα του (α)
Α-4. (α) Έστω Χ τοπολογικός χώρος ,
 συνεκτικό για κάθε
συνεκτικό για κάθε  και
και 
Αποδείξτε ότι το σύνολο
 είναι συνεκτικό.
είναι συνεκτικό.(β) Αν Χ και Y είναι τοπολογικοί χώροι συνεκτικοί , αποδείξτε (με την βοήθεια του (α) ) ότι και το γινόμενο Χ*Y είναι χώρος συνεκτικός.
Β-1. (α) Περιγράψτε λεπτομερώς την τοπολογία Καρτεσιανό γινόμενο.
(β) Αν
 είναι χώρος
είναι χώρος  για κάθε
για κάθε  , αποδείξτε ότι και
, αποδείξτε ότι και  είναι χώρος
είναι χώρος 
Β-2. (α) Δώστε τον ορισμό του δικτύου και της συγκλίσεως δικτύου σε ένα τοπολογικό χώρο.
(β) Έστω Χ τοπολογικός χώρος
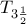 . Αποδείξτε ότι ένα δίκτυο
. Αποδείξτε ότι ένα δίκτυο 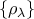 στον Χ συγλίνει σε ένα σημείο ρ, αν και μόνο αν
στον Χ συγλίνει σε ένα σημείο ρ, αν και μόνο αν 
για κάθε
 με f συνεχή.
με f συνεχή.Β-3. (α) Έστω Χ τοπολογικός χώρος,
 κλειστά υποσύνολα του Χ ώστε:
κλειστά υποσύνολα του Χ ώστε: . Αποδείξτε ότι μια συνάρτηση
. Αποδείξτε ότι μια συνάρτηση  είναι συνεχής αν και μόνο αν
είναι συνεχής αν και μόνο αν  είναι συνεχής για κάθε i = 1,2,...,ν
είναι συνεχής για κάθε i = 1,2,...,ν(β) Έστω Χ τοπολογικός χώρος ,
 κλειστό για κάθε
κλειστό για κάθε  και
και  ώστε για κάθε
ώστε για κάθε  υπάρχει U περιοχή του x ώστε το σύνολο
υπάρχει U περιοχή του x ώστε το σύνολο  να είναι πεπερασμένο. Αποδείξτε ότι μια συνάρτηση
να είναι πεπερασμένο. Αποδείξτε ότι μια συνάρτηση  είναι συνεχής αν και μόνο αν
είναι συνεχής αν και μόνο αν  συνεχής για κάθε
συνεχής για κάθε 
Γ-1. (α) Έστω (Χ,ρ) μετρικός χώρος , Α, Β κλειστά μη κενά υποσύνολα του Χ ώστε
 και Α συμπαγές. Αποδείξτε ότι
και Α συμπαγές. Αποδείξτε ότι 
(β) Δώστε παράδειγμα στον μετρικό χώρο
 δύο μη κενών ξένων κλειστών υποσυνόλων Α,Β ώστε
δύο μη κενών ξένων κλειστών υποσυνόλων Α,Β ώστε ρ(Α,Β)=0.
Γ-2 (α) 'Εστω Χ συμπαγής μετρικός χώρος και
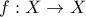 ισομετρία, δηλαδή για κάθε
ισομετρία, δηλαδή για κάθε  ,
, . Αποδείξτε ότι η f είναι επί.
. Αποδείξτε ότι η f είναι επί.(Υποθέσατε ότι
 (n όροι))
(n όροι))(Να απαντήσετε σε 2 θέματα της ομάδας Α, 2 της Β και σε 1 της Γ)


 . Αφού ο
. Αφού ο  είναι πρώτος αριθμήσιμος υπάρχει ακολουθία
είναι πρώτος αριθμήσιμος υπάρχει ακολουθία  ανοικτών συνόλων ώστε κάθε ανοικτό σύνολο που περιέχει το
ανοικτών συνόλων ώστε κάθε ανοικτό σύνολο που περιέχει το  περιέχει και κάποιο από τα
περιέχει και κάποιο από τα  . Μπορούμε να υποθέσουμε ότι
. Μπορούμε να υποθέσουμε ότι  .
. το
το  είναι μη κενό. Έστω λοιπόν
είναι μη κενό. Έστω λοιπόν  . Ισχυρίζομαι ότι
. Ισχυρίζομαι ότι  . Πρέπει να δείξω ότι για κάθε ανοικτο
. Πρέπει να δείξω ότι για κάθε ανοικτο  που περιέχει το
που περιέχει το  , ώστε
, ώστε  για κάθε
για κάθε  . Αυτό όμως είναι άμεσο αφού από τον ορισμό της ακολουθίας
. Αυτό όμως είναι άμεσο αφού από τον ορισμό της ακολουθίας  , και άρα
, και άρα 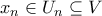 για κάθε
για κάθε  με την cocountable τοπολογία. Δηλαδή τα κλειστά σύνολα είναι το
με την cocountable τοπολογία. Δηλαδή τα κλειστά σύνολα είναι το ![A = [0,1] A = [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/5091c91e2fe9a25b2aea47dd5f673a7f.png) . Τότε απαραίτητα
. Τότε απαραίτητα  . Έστω
. Έστω  και
και  ακολουθία στοιχείων του
ακολουθία στοιχείων του  . Θα δείξουμε ότι
. Θα δείξουμε ότι  . Παίρνουμε το ανοικτό σύνολο
. Παίρνουμε το ανοικτό σύνολο  το οποίο περιέχει το
το οποίο περιέχει το  , τότε για κάθε ανοικτό σύνολο
, τότε για κάθε ανοικτό σύνολο  με
με  υπάρχει ανοικτό
υπάρχει ανοικτό 

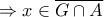
 δεν είναι ανοικτό, τότε θα υπάρχει
δεν είναι ανοικτό, τότε θα υπάρχει  , ώστε για κάθε ανοικτή περιοχή
, ώστε για κάθε ανοικτή περιοχή 
 , άτοπο.
, άτοπο. και
και 
 , τότε
, τότε  .
.
 θα έχειν συγκλινουσα υπακολουθία
θα έχειν συγκλινουσα υπακολουθία  , αδύνατο γιατί
, αδύνατο γιατί (
( )
) τότε υπάρχει ακολουθία
τότε υπάρχει ακολουθία  με
με  . Μετά θεωρούμε συγκλίνουσα υπακολουθία της
. Μετά θεωρούμε συγκλίνουσα υπακολουθία της  Οι λεπτομέρεις είναι άμεσες.
Οι λεπτομέρεις είναι άμεσες.
 δεν είναι συνεκτικό. Τότε υπάρχουν μη κενά ανοικτά υποσύνολα
δεν είναι συνεκτικό. Τότε υπάρχουν μη κενά ανοικτά υποσύνολα  στο
στο  και
και  . Για κάθε
. Για κάθε 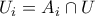 και
και  . Τα
. Τα  είναι ανοικτά υποσύνολα του
είναι ανοικτά υποσύνολα του  και προφανώς
και προφανώς  . Επίσης
. Επίσης 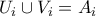 . Πράγματι το
. Πράγματι το  είναι προφανές ενώ για το αντίστροφο, αν
είναι προφανές ενώ για το αντίστροφο, αν  τότε χωρίς βλάβη της γενικότητας
τότε χωρίς βλάβη της γενικότητας  . Αρκεί λοιπόν να δείξω ότι για κάποιο
. Αρκεί λοιπόν να δείξω ότι για κάποιο  .
.  . Χωρίς βλάβη της γενικότητας
. Χωρίς βλάβη της γενικότητας  και άρα
και άρα  για κάθε
για κάθε  . Αυτό όμως είναι άμεσο αφού το
. Αυτό όμως είναι άμεσο αφού το  έχουμε
έχουμε  για κάποιο
για κάποιο  αφού τότε θα είχαμε
αφού τότε θα είχαμε  και άρα
και άρα  . Άρα
. Άρα  και άρα
και άρα  είναι μη κενά αλλιώς το συμπέρασμα είναι προφανές αφού τότε θα είχαμε
είναι μη κενά αλλιώς το συμπέρασμα είναι προφανές αφού τότε θα είχαμε 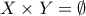 το οποίο εξ' ορισμού είναι συνεκτικό
το οποίο εξ' ορισμού είναι συνεκτικό τα
τα 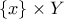 και
και  είναι συνεκτικά και έχουν μη κενή τομή άρα η ένωσή τους
είναι συνεκτικά και έχουν μη κενή τομή άρα η ένωσή τους  είναι συνεκτική. Κρατούμε τώρα το
είναι συνεκτική. Κρατούμε τώρα το  το
το  είναι μη κενό, τότε η ένωση
είναι μη κενό, τότε η ένωση 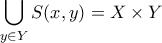 είναι συνεκτική όπως θέλαμε να δείξουμε.
είναι συνεκτική όπως θέλαμε να δείξουμε. ένα κλειστό υποσύνολο του
ένα κλειστό υποσύνολο του 
 είναι κλειστό, λόγω της συνέχειας των
είναι κλειστό, λόγω της συνέχειας των  , θα είναι κλειστό και το
, θα είναι κλειστό και το  , συνεπώς το ζητούμενο απεδείχθη.
, συνεπώς το ζητούμενο απεδείχθη.

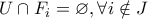 , όπου
, όπου  και
και  το υποσύνολο του
το υποσύνολο του  το οποίο
το οποίο
 υπάρχει ανοικτό υποσύνολο
υπάρχει ανοικτό υποσύνολο  του
του  με
με 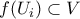
 , ώστε
, ώστε 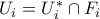
 , είναι μία ανοικτή
, είναι μία ανοικτή , άρα η
, άρα η  είναι συνεχής στο
είναι συνεχής στο