Λύσεις Μαθ. κατ. 2009
Re: Λύσεις Μαθ. κατ. 2009
Αυτό ακριβώς αναφέρει και ο κύριος Ιωσηφίδης , ότι αφού στην εκφώνηση του θέματος δεν αναφέρει ότι το α είναι μοναδικό πρέπει να το δείξουμε
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3342
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Λύσεις Μαθ. κατ. 2009
Καταλαβαινω που το πας, υπαρχει ομως μια καιρια διαφορα αναμεσα στην a^x - ln(x+1) και στην (x-a)^2 + 1 : στην πρωτη περιπτωση a^0 - ln(0+1) = 1 (*ανεξαρτητο του a*), στην δευτερη περιπτωση (0-a)^2 + 1 = a^2 + 1 (*μη ανεξαρτητο του a*). [Στην πρωτη περιπτωση μπορουμε να πουμε πως εχουμε τοπικο ελαχιστο στο x = 0 ανεξαρτητως της τιμης του a, στην δευτερη περιπτωση οχι -- και βεβαια οπως εχει δοθει το (Α) πιο πανω ... το ζητουμενο δεν ισχυει καν, εχουμε εσφαλμενο προβλημα*.]lehrer έγραψε:Σωστός. Ας δούμε τώρα ξανά το θέμα χωρίς την αρχική συνθήκη όπως δίνονταν στις εξετάσεις.
Δίνεται η συνάρτηση
f(x)=(x-α)^2+1
Α ) Αν ισχύει f(x)>=1 να δειχτεί ότι α=0
Ερώτηση : Είναι το α μοναδικό; Ή μήπως είναι άπειρα;
*αν βεβαια τροποποιουσαμε το (Α) σε "Αν ισχύει f(x) >= a^2 + 1 (για καθε x) να δειχτεί ότι a = 0" τοτε ... κανενα προβλημα! (Διοτι θα επρεπε να εχουμε x^2 - ax >= 0 για καθε x, δηλαδη x(x-a) >= 0 για καθε x, κατι που ισχυει *μονον* οταν a = 0. H, καταφευγοντας στον Fermat (που δεν χρειαζεται σ' αυτην την περιπτωση), επειδη εχουμε τοπικο ελαχιστο στο x = 0 προκυπτει f'(0) = 0 και 2(0-a) = 0 αρα a = 0.)
Γιωργος Μπαλογλου
Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Re: Λύσεις Μαθ. κατ. 2009
Καλημέραlehrer έγραψε:Σωστός. Ας δούμε τώρα ξανά το θέμα χωρίς την αρχική συνθήκη όπως δίνονταν στις εξετάσεις.
Δίνεται η συνάρτηση
f(x)=(x-α)^2+1
Α ) Αν ισχύει f(x)>=1 να δειχτεί ότι α=0
Ερώτηση : Είναι το α μοναδικό; Ή μήπως είναι άπειρα;
Δεν υφίσταται το ερώτημα (δεν μπορεί με τα δεδομένα που υπάρχουν να ζητάμε να αποδειχθεί ότι α=0, άρα δεν έχει νόημα να το κουβεντιάζουμε. )
Η σχέση
 ισχύει για κάθε x και α στο R και δεν χρειάζεται κανένας Fermat για τους μαθητές της Α΄ Λυκείου.
ισχύει για κάθε x και α στο R και δεν χρειάζεται κανένας Fermat για τους μαθητές της Α΄ Λυκείου.Φιλικά
Γιώργος
Γιώργος Ροδόπουλος
Re: Λύσεις Μαθ. κατ. 2009
Ασ το δουμε λιγο και με τη μορφη συστηματος. Ας πουμε οτι βρισκαμε διαφορες συνθηκες για το α, π.χ.
α=0
2α+5=5

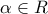

Αν ξερουμε οτι ειναι συμβιβαστο, δηλαδη οτι η ασκηση ειναι σωστη, δεν χρειαζεται να ελεγξουμε τιποτα. α=0 απο την πρωτη και τελειωσε
θα πηγαινε κανεις να βρει και τις λυσεις π.χ. της τελευταιας και να αναρωτηθει μηπως ειναι και αυτες αποδεκτές(εκτος του α=0)?. Οχι, διοτι πρεπει να συναληθευουν ολες οι συνθηκες, αρα και η πρωτη, η οποια αληθευει μονο οταν α=0.
α=0
2α+5=5

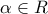

Αν ξερουμε οτι ειναι συμβιβαστο, δηλαδη οτι η ασκηση ειναι σωστη, δεν χρειαζεται να ελεγξουμε τιποτα. α=0 απο την πρωτη και τελειωσε
θα πηγαινε κανεις να βρει και τις λυσεις π.χ. της τελευταιας και να αναρωτηθει μηπως ειναι και αυτες αποδεκτές(εκτος του α=0)?. Οχι, διοτι πρεπει να συναληθευουν ολες οι συνθηκες, αρα και η πρωτη, η οποια αληθευει μονο οταν α=0.
Re: Λύσεις Μαθ. κατ. 2009
Και βεβαια, δεν γραφω κατι καινουριο, απλως δινω παραδειγματα. Ολα αυτα τα ειχαν γραψει αρκετα πιο νωρις στη συζητηση αλλα μελη.
Re: Λύσεις Μαθ. κατ. 2009
Συμφωνω απολυτα, για την περιπτωση των εξετασεων γραφωhsiodos έγραψε:Καλημέραlehrer έγραψε:Σωστός. Ας δούμε τώρα ξανά το θέμα χωρίς την αρχική συνθήκη όπως δίνονταν στις εξετάσεις.
Δίνεται η συνάρτηση
f(x)=(x-α)^2+1
Α ) Αν ισχύει f(x)>=1 να δειχτεί ότι α=0
Ερώτηση : Είναι το α μοναδικό; Ή μήπως είναι άπειρα;
Δεν υφίσταται το ερώτημα (δεν μπορεί με τα δεδομένα που υπάρχουν να ζητάμε να αποδειχθεί ότι α=0, άρα δεν έχει νόημα να το κουβεντιάζουμε. )
Η σχέσηισχύει για κάθε x και α στο R και δεν χρειάζεται κανένας Fermat για τους μαθητές της Α΄ Λυκείου.
Φιλικά
Γιώργος
Re: Λύσεις Μαθ. κατ. 2009
Νομίζω ότι η συζήτηση για το συγκεκριμένο θέμα συνεχίζεται χωρίς να υπάρχει λόγος και οι μαθητές μας έχουν αρχίσει να μπερδεύονται. Μπορεί να κάνουμε διάλογο όπως σωστά λέει ο συνάδελφος κ. Μαυρογάννης, όμως το θέμα είναι πλέον ξεκάθαρο και έχει απαντηθεί αναλυτικά από τον Α. Κυριακόπουλο. Αν μία αληθής πρόταση p μέσα από έγκυρους μαθηματικούς συλλογισμούς οδηγεί στην q, τότε η συνεπαγωγή είναι αληθής αλλά και η q και η απόδειξη είναι πλήρης. Αποτελεί βασικό κανόνα της μαθηματικής λογικής. Αν τον αποδεχόμαστε τότε όλα τα δήθεν αντιπαραδείγματα έχουν λάθος στην διατύπωση ή την επιχειρηματολογία τους. Διαφορετικά, πρέπει να αρχίζουμε να ψάχνουμε για νέους κανόνες στα μαθηματικά.
Σ. Ορφανάκης
Σ. Ορφανάκης
Σπύρος
Re: Λύσεις Μαθ. κατ. 2009
Αγαπητοί συνάδελφοι,
Με αφορμή το εξής σχόλιο του κ. Α.Κυριακόπουλου :
«3) Γράφεις: « Ανεξάρτητα αν είναι δυνατόν ή όχι να βρούμε δύο διαφορετικές τιμές του α, πρέπει να υπάρξει αιτιολόγηση. Αυτό λέει ο Λεωνίδας». Θα μου επιτρέψεις να σου πω ότι αυτό ακριβώς είναι το λάθος του Λεωνίδα. Τι να αιτιολογήσουμε; Αφού αποδείξαμε αυτό που μας ζητούσαν δεν τελειώσαμε; Οτιδήποτε άλλο προσθέσουμε, όχι μόνο θα είναι λάθος, αλλά θα δείχνει ότι δεν έχουμε κατανοήσει την έννοια της απόδειξης στα μαθηματικά.»
Θέλω να δείτε τις εξής ασκήσεις:
ΑΣΚΗΣΗ 1:
Δίνεται η συνάρτηση
f(x)=α^x - ln(x+1) , x>-1
Αν η f(x) παρουσιάζει τοπικό ακρότατο στο 0, να αποδείξετε ότι α=e.
ΑΣΚΗΣΗ 2:
Δίνεται η συνάρτηση
f(x)= α^x - ln(x+1) , x>-1
Αν η f(x) παρουσιάζει τοπικό ελάχιστο στο 0, να αποδείξετε ότι α=e.
ΑΣΚΗΣΗ 3
Δίνεται η συνάρτηση
f(x)= α^x - ln(x+1) , x>-1
Αν η f(x) παρουσιάζει ολικό ελάχιστο στο 0, να αποδείξετε ότι α=e.
Οι τρεις αυτές ασκήσεις είναι εντελώς διαφορετικές ωστόσο λύνονται με τον ίδιο τρόπο!!!
Ξεκινάμε λέγοντας ότι πρέπει f΄(0)=0=> … =>α=e.
Δηλαδή, αγαπητοί συνάδελφοι είτε λέμε ότι η f παρουσιάζει τοπικό ακρότατο, είτε τοπικό ελάχιστο, είτε ολικό ελάχιστο η αποδεικτική διαδικασία είναι ακριβώς η ίδια!!! Μα καλά, 3 διαφορετικές ασκήσεις, λύνονται με τον ίδιο ακριβώς τρόπο; Το γεγονός ότι η άσκηση 2 έχει ένα παραπάνω δεδομένο από την 1 δεν επηρεάζει τη λύση ; Όμοια και για τις ασκήσεις 2 και 3. Δεν είναι αυτό περίεργο; Χρησιμοποιήθηκαν όλα τα δεδομένα μας πλήρως στις λύσεις αυτές για τις ασκήσεις 2 και 3;
Για αυτό το λόγο διαφωνώ πλήρως με αυτά που είπε ο συνάδελφος. Το ίδιο συμβαίνει και με την άσκηση 3 Α. Αν η άσκηση έδινε τοπικό ακρότατο στο 0 τι θα άλλαζε στην απόδειξη; ΤΙΠΟΤΑ. Άρα η λύση του 3 Α σίγουρα δεν τελειώνει εδώ.
Φιλικά
Λ. Ιωσηφίδης
Με αφορμή το εξής σχόλιο του κ. Α.Κυριακόπουλου :
«3) Γράφεις: « Ανεξάρτητα αν είναι δυνατόν ή όχι να βρούμε δύο διαφορετικές τιμές του α, πρέπει να υπάρξει αιτιολόγηση. Αυτό λέει ο Λεωνίδας». Θα μου επιτρέψεις να σου πω ότι αυτό ακριβώς είναι το λάθος του Λεωνίδα. Τι να αιτιολογήσουμε; Αφού αποδείξαμε αυτό που μας ζητούσαν δεν τελειώσαμε; Οτιδήποτε άλλο προσθέσουμε, όχι μόνο θα είναι λάθος, αλλά θα δείχνει ότι δεν έχουμε κατανοήσει την έννοια της απόδειξης στα μαθηματικά.»
Θέλω να δείτε τις εξής ασκήσεις:
ΑΣΚΗΣΗ 1:
Δίνεται η συνάρτηση
f(x)=α^x - ln(x+1) , x>-1
Αν η f(x) παρουσιάζει τοπικό ακρότατο στο 0, να αποδείξετε ότι α=e.
ΑΣΚΗΣΗ 2:
Δίνεται η συνάρτηση
f(x)= α^x - ln(x+1) , x>-1
Αν η f(x) παρουσιάζει τοπικό ελάχιστο στο 0, να αποδείξετε ότι α=e.
ΑΣΚΗΣΗ 3
Δίνεται η συνάρτηση
f(x)= α^x - ln(x+1) , x>-1
Αν η f(x) παρουσιάζει ολικό ελάχιστο στο 0, να αποδείξετε ότι α=e.
Οι τρεις αυτές ασκήσεις είναι εντελώς διαφορετικές ωστόσο λύνονται με τον ίδιο τρόπο!!!
Ξεκινάμε λέγοντας ότι πρέπει f΄(0)=0=> … =>α=e.
Δηλαδή, αγαπητοί συνάδελφοι είτε λέμε ότι η f παρουσιάζει τοπικό ακρότατο, είτε τοπικό ελάχιστο, είτε ολικό ελάχιστο η αποδεικτική διαδικασία είναι ακριβώς η ίδια!!! Μα καλά, 3 διαφορετικές ασκήσεις, λύνονται με τον ίδιο ακριβώς τρόπο; Το γεγονός ότι η άσκηση 2 έχει ένα παραπάνω δεδομένο από την 1 δεν επηρεάζει τη λύση ; Όμοια και για τις ασκήσεις 2 και 3. Δεν είναι αυτό περίεργο; Χρησιμοποιήθηκαν όλα τα δεδομένα μας πλήρως στις λύσεις αυτές για τις ασκήσεις 2 και 3;
Για αυτό το λόγο διαφωνώ πλήρως με αυτά που είπε ο συνάδελφος. Το ίδιο συμβαίνει και με την άσκηση 3 Α. Αν η άσκηση έδινε τοπικό ακρότατο στο 0 τι θα άλλαζε στην απόδειξη; ΤΙΠΟΤΑ. Άρα η λύση του 3 Α σίγουρα δεν τελειώνει εδώ.
Φιλικά
Λ. Ιωσηφίδης
Re: Λύσεις Μαθ. κατ. 2009
Δηλαδή, αν τρεις αληθείς προτάσεις p1, p2, p3 με μαθηματικούς συλλογισμούς συνεπάγονται την πρόταση q,
τότε δεν πρέπει να είμαστε σίγουροι για την πληρότητα της απόδειξης. Με άλλα λόγια μπαίνει θέμα ορθότητας της μαθηματικής λογικής. Προφανώς, διαφωνώ με αυτό συνάδελφε.
τότε δεν πρέπει να είμαστε σίγουροι για την πληρότητα της απόδειξης. Με άλλα λόγια μπαίνει θέμα ορθότητας της μαθηματικής λογικής. Προφανώς, διαφωνώ με αυτό συνάδελφε.
Σπύρος
Re: Λύσεις Μαθ. κατ. 2009
Aγαπητέ Λεωνίδαiosifile έγραψε:Αγαπητοί συνάδελφοι,
Με αφορμή το εξής σχόλιο του κ. Α.Κυριακόπουλου :
«3) Γράφεις: « Ανεξάρτητα αν είναι δυνατόν ή όχι να βρούμε δύο διαφορετικές τιμές του α, πρέπει να υπάρξει αιτιολόγηση. Αυτό λέει ο Λεωνίδας». Θα μου επιτρέψεις να σου πω ότι αυτό ακριβώς είναι το λάθος του Λεωνίδα. Τι να αιτιολογήσουμε; Αφού αποδείξαμε αυτό που μας ζητούσαν δεν τελειώσαμε; Οτιδήποτε άλλο προσθέσουμε, όχι μόνο θα είναι λάθος, αλλά θα δείχνει ότι δεν έχουμε κατανοήσει την έννοια της απόδειξης στα μαθηματικά.»
Θέλω να δείτε τις εξής ασκήσεις:
ΑΣΚΗΣΗ 1:
Δίνεται η συνάρτηση
f(x)=α^x - ln(x+1) , x>-1
Αν η f(x) παρουσιάζει τοπικό ακρότατο στο 0, να αποδείξετε ότι α=e.
ΑΣΚΗΣΗ 2:
Δίνεται η συνάρτηση
f(x)= α^x - ln(x+1) , x>-1
Αν η f(x) παρουσιάζει τοπικό ελάχιστο στο 0, να αποδείξετε ότι α=e.
ΑΣΚΗΣΗ 3
Δίνεται η συνάρτηση
f(x)= α^x - ln(x+1) , x>-1
Αν η f(x) παρουσιάζει ολικό ελάχιστο στο 0, να αποδείξετε ότι α=e.
Οι τρεις αυτές ασκήσεις είναι εντελώς διαφορετικές ωστόσο λύνονται με τον ίδιο τρόπο!!!
Ξεκινάμε λέγοντας ότι πρέπει f΄(0)=0=> … =>α=e.
Δηλαδή, αγαπητοί συνάδελφοι είτε λέμε ότι η f παρουσιάζει τοπικό ακρότατο, είτε τοπικό ελάχιστο, είτε ολικό ελάχιστο η αποδεικτική διαδικασία είναι ακριβώς η ίδια!!! Μα καλά, 3 διαφορετικές ασκήσεις, λύνονται με τον ίδιο ακριβώς τρόπο; Το γεγονός ότι η άσκηση 2 έχει ένα παραπάνω δεδομένο από την 1 δεν επηρεάζει τη λύση ; Όμοια και για τις ασκήσεις 2 και 3. Δεν είναι αυτό περίεργο; Χρησιμοποιήθηκαν όλα τα δεδομένα μας πλήρως στις λύσεις αυτές για τις ασκήσεις 2 και 3;
Για αυτό το λόγο διαφωνώ πλήρως με αυτά που είπε ο συνάδελφος. Το ίδιο συμβαίνει και με την άσκηση 3 Α. Αν η άσκηση έδινε τοπικό ακρότατο στο 0 τι θα άλλαζε στην απόδειξη; ΤΙΠΟΤΑ. Άρα η λύση του 3 Α σίγουρα δεν τελειώνει εδώ.
Φιλικά
Λ. Ιωσηφίδης
Η λύση του 3Α έχει τελειώσει εδώ και καιρό.
Έχω να παρατηρήσω τα εξής:
1) Δεν έχεις αντιτάξει κανένα μαθηματικό επιχείρημα στα όσα συγκεκριμένα έχει γράψει ο Α.Κυριακόπουλος και οι άλλοι συνάδελφοι που έχουμε ασχοληθεί με το θέμα αυτό.
Προβάλεις μόνο αίολους ισχυρισμούς.
2) Οι τρεις ασκήσεις που παραθέτεις είναι ακριβώς ίδιες , δεν έχουν επί της ουσίας τίποτα το διαφορετικό.
Αλλάζεις την μορφή του δεδομένου (το κάνεις ολοένα και πιο ισχυρό , το ολικό είναι και τοπικό ελάχιστο και αυτό είναι τοπικό ακρότατο) αλλά αυτό δεν επηρεάζει στο παραμικρό την αποδεικτική διαδικασία που έχει χιλιοειπωθεί.
3) Ούτε λίγο ούτε πολύ μας ζητάς το εξής:
Σε ένα μαθητή της Α Λυκείου δίνουμε το ερώτημα
Αν f(x) = 2x + α και f(0) = 1 να αποδείξετε ότι α = 1 .
Ο μαθητής (και σωστά) από την f(0) = 1 βρίσκει πράγματι ότι α=1.
Εμείς τώρα πρέπει να του πούμε (σύμφωνα με αυτά που ισχυρίζεσαι)
'' Η απόδειξη δεν είναι πλήρης. Γιατί μπορεί να υπάρχει κάποιο
 με
με  και έτσι μπορεί να προκύψει διαφορετική τιμή του α , άρα...(δεν συνεχίζω) ''
και έτσι μπορεί να προκύψει διαφορετική τιμή του α , άρα...(δεν συνεχίζω) ''Αυτό δεν είναι Μαθηματικός Λογισμός αλλά Παραμαθηματικός παραλογισμός.
Φιλικά
Γιώργος
Γιώργος Ροδόπουλος
Re: Λύσεις Μαθ. κατ. 2009
Αυτό που προσπαθώ να πω είναι ότι αν βρούμε ένα α δεν σημαίνει ότι αυτό είναι μοναδικό. Είναι μοναδικό για την συνάρτηση αλλά όχι και για την συγκεκριμένη οικογένεια των συναρτήσεων. Για άλλο α μπορεί να υπάρχει συνάρτηση που να ικανοποιεί τις υποθέσεις του προβλήματος
Για τον διορατικότατο κύριο Μπάλογλου ας δούμε ξανά το θέμα :
Δίνεται η συνάρτηση
f(x)=(αx)^2+1
Αν f(x)>=1 βρείτε το α
Απ ότι βλέπετε υπάρχουν άπειρα α. Αν τώρα ο εξεταστής μας ζητούσε ότι α=3 εμείς θα έπρεπε να απορίψουμε όλες τις υπόλοιπες. Ή αν βρίσκαμε μια θα έπρεπε να δείξουμε ότι είναι και η μοναδική. Αυτό κάνει ο κύριος Ιωσηφίδης
Για τον διορατικότατο κύριο Μπάλογλου ας δούμε ξανά το θέμα :
Δίνεται η συνάρτηση
f(x)=(αx)^2+1
Αν f(x)>=1 βρείτε το α
Απ ότι βλέπετε υπάρχουν άπειρα α. Αν τώρα ο εξεταστής μας ζητούσε ότι α=3 εμείς θα έπρεπε να απορίψουμε όλες τις υπόλοιπες. Ή αν βρίσκαμε μια θα έπρεπε να δείξουμε ότι είναι και η μοναδική. Αυτό κάνει ο κύριος Ιωσηφίδης
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3342
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Λύσεις Μαθ. κατ. 2009
Ας δουμε τα τρια προβληματα απο την αρχη:lehrer έγραψε:Αυτό που προσπαθώ να πω είναι ότι αν βρούμε ένα α δεν σημαίνει ότι αυτό είναι μοναδικό. Είναι μοναδικό για την συνάρτηση αλλά όχι και για την συγκεκριμένη οικογένεια των συναρτήσεων. Για άλλο α μπορεί να υπάρχει συνάρτηση που να ικανοποιεί τις υποθέσεις του προβλήματος
Για τον διορατικότατο κύριο Μπάλογλου ας δούμε ξανά το θέμα :
Δίνεται η συνάρτηση
f(x)=(αx)^2+1
Αν f(x)>=1 βρείτε το α
Απ ότι βλέπετε υπάρχουν άπειρα α. Αν τώρα ο εξεταστής μας ζητούσε ότι α=3 εμείς θα έπρεπε να απορίψουμε όλες τις υπόλοιπες. Ή αν βρίσκαμε μια θα έπρεπε να δείξουμε ότι είναι και η μοναδική. Αυτό κάνει ο κύριος Ιωσηφίδης
(1)
Δίνεται η συνάρτηση
f(x)=(x-α)^2+1 και f(0)=1
Αν f(x)>=1 να δειχτεί ότι α=0
(2)
Δίνεται η συνάρτηση
f(x)=(x-α)^2+1
Αν f(x)>=1 να δειχτεί ότι α=0
(3)
Δίνεται η συνάρτηση
f(x)=(αx)^2+1
Αν f(x)>=1 βρείτε το α
Το (1) ειναι σωστο, αν και το α=0 προκυπτει *απευθειας* απο την σχεση f(0)=1 *και μονον* -- περιττευει δηλαδη η υποθεση f(x)>=1, η οποια παντως ισχυει ουτως η αλλως και ανεξαρτητως του α.
Τα (2) και (3) ειναι εξισου εσφαλμενα: η ανισοτητα f(x)>=1 ισχυει και παλι ουτως η αλλως και ανεξαρτητως του α, αρα δεν μπορουμε να βρουμε το α -- να το πουμε αλλοιως, η υποθεση f(x)>=1 αληθευει για ολα τα α.
Η μονη διαφορα αναμεσα σε (2) και (3) ειναι οτι το μεν (2) μπορει να τροποποιηθει σε αποδεκτο προβλημα (οπως εδειξα σε προηγουμενη αναρτηση), το δε (3) δεν σωζεται με τιποτα!
Γιωργος Μπαλόγλου
Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
-
k-ser
- Δημοσιεύσεις: 870
- Εγγραφή: Σάβ Δεκ 20, 2008 10:22 am
- Τοποθεσία: Μουζάκι Καρδίτσας
- Επικοινωνία:
Re: Λύσεις Μαθ. κατ. 2009
Είπα να μην επανέλθω μα...
Η άσκηση δεν ζητάει καμιά εύρεση της τιμής του α.
Η άσκηση ζητάει την απόδειξη - την "αλήθεια" μιας συνεπαγωγής: Αν Α τότε Β.
Για την απόδειξη αυτής της συνεπαγωγής δεν χρειάζεται να εξετάσουμε αν η Α είναι ψευδής γιατί τότε, η αλήθεια της συνεπαγωγής είναι προφανής.
Υποθέτουμε έτσι, ότι Α αληθής και φτάνουμε, χρησιμοποιώντας αυτή την υπόθεση και τις αληθείς μαθηματικές προτάσεις, ότι και Β αληθής.
Μπορούμε να αποδείξουμε αυτή την συνεπαγωγή , εφόσον αυτό είναι εφικτό, και με τον εξής τρόπο:
Αποδεικνύουμε ότι η Α είναι ψευδής.
Παράδειγμα:
Να δειχθεί ότι:
Αν η συνάρτηση ,
,  παρουσιάζει μέγιστο στο 1 τότε
παρουσιάζει μέγιστο στο 1 τότε  .
.
Απόδειξη:
1ος τρόπος: με θεώρημα Fermat.
2ος τρόπος:
Η συνάρτηση αυτή δεν έχει μέγιστη τιμή.
Η υπόθεση είναι λανθασμένη οπότε η συνεπαγωγή είναι αληθής!
Η άσκηση δεν ζητάει καμιά εύρεση της τιμής του α.
Η άσκηση ζητάει την απόδειξη - την "αλήθεια" μιας συνεπαγωγής: Αν Α τότε Β.
Για την απόδειξη αυτής της συνεπαγωγής δεν χρειάζεται να εξετάσουμε αν η Α είναι ψευδής γιατί τότε, η αλήθεια της συνεπαγωγής είναι προφανής.
Υποθέτουμε έτσι, ότι Α αληθής και φτάνουμε, χρησιμοποιώντας αυτή την υπόθεση και τις αληθείς μαθηματικές προτάσεις, ότι και Β αληθής.
Μπορούμε να αποδείξουμε αυτή την συνεπαγωγή , εφόσον αυτό είναι εφικτό, και με τον εξής τρόπο:
Αποδεικνύουμε ότι η Α είναι ψευδής.
Παράδειγμα:
Να δειχθεί ότι:
Αν η συνάρτηση
 ,
,  παρουσιάζει μέγιστο στο 1 τότε
παρουσιάζει μέγιστο στο 1 τότε  .
.Απόδειξη:
1ος τρόπος: με θεώρημα Fermat.
2ος τρόπος:
Η συνάρτηση αυτή δεν έχει μέγιστη τιμή.
Η υπόθεση είναι λανθασμένη οπότε η συνεπαγωγή είναι αληθής!
Κώστας Σερίφης
- Ραϊκόφτσαλης Θωμάς
- Δημοσιεύσεις: 1112
- Εγγραφή: Κυρ Δεκ 21, 2008 12:01 am
- Τοποθεσία: Άλιμος, Αθήνα
- Επικοινωνία:
Re: Λύσεις Μαθ. κατ. 2009
Αγαπητέ Λεωνίδα, αν είχες ασχοληθεί με την άσκηση που είχα στείλει και είναι η εξής:iosifile έγραψε:Αγαπητοί συνάδελφοι,
Οι τρεις αυτές ασκήσεις είναι εντελώς διαφορετικές ωστόσο λύνονται με τον ίδιο τρόπο!!!
Ξεκινάμε λέγοντας ότι πρέπει f΄(0)=0=> … =>α=e.
Δηλαδή, αγαπητοί συνάδελφοι είτε λέμε ότι η f παρουσιάζει τοπικό ακρότατο, είτε τοπικό ελάχιστο, είτε ολικό ελάχιστο η αποδεικτική διαδικασία είναι ακριβώς η ίδια!!! Μα καλά, 3 διαφορετικές ασκήσεις, λύνονται με τον ίδιο ακριβώς τρόπο; Το γεγονός ότι η άσκηση 2 έχει ένα παραπάνω δεδομένο από την 1 δεν επηρεάζει τη λύση ; Όμοια και για τις ασκήσεις 2 και 3. Δεν είναι αυτό περίεργο; Χρησιμοποιήθηκαν όλα τα δεδομένα μας πλήρως στις λύσεις αυτές για τις ασκήσεις 2 και 3;
Για αυτό το λόγο διαφωνώ πλήρως με αυτά που είπε ο συνάδελφος. Το ίδιο συμβαίνει και με την άσκηση 3 Α. Αν η άσκηση έδινε τοπικό ακρότατο στο 0 τι θα άλλαζε στην απόδειξη; ΤΙΠΟΤΑ. Άρα η λύση του 3 Α σίγουρα δεν τελειώνει εδώ.
Φιλικά
Λ. Ιωσηφίδης
Έστω η συνάρτηση
 \displaystyle f(x) = \alpha \eta \mu (\alpha x) - 2(\alpha + 1)\eta \mu 2(\alpha + 1)x
\displaystyle f(x) = \alpha \eta \mu (\alpha x) - 2(\alpha + 1)\eta \mu 2(\alpha + 1)x , όπου
, όπου  \displaystyle \alpha \in \mathbb{R}
\displaystyle \alpha \in \mathbb{R} .
.Αν ισχύει
 \displaystyle f(x) \geqslant 0
\displaystyle f(x) \geqslant 0 για κάθε
για κάθε  \displaystyle x \in \mathbb{R}
\displaystyle x \in \mathbb{R} , να βρεθούν οι τιμές του α,
, να βρεθούν οι τιμές του α,θα έβλεπες ότι για
 \displaystyle \alpha = - \frac{2}
\displaystyle \alpha = - \frac{2}{3}
 ή α=-2, η συνάρτηση είναι σταθερή (f(x)=0, πρέπει να κάνεις επαλήθευση των τιμών του α για να το δεις), οπότε παρουσιάζονται σε άπειρες θέσεις τα τοπικά ή ολικά μέγιστα ή ελάχιστα.
ή α=-2, η συνάρτηση είναι σταθερή (f(x)=0, πρέπει να κάνεις επαλήθευση των τιμών του α για να το δεις), οπότε παρουσιάζονται σε άπειρες θέσεις τα τοπικά ή ολικά μέγιστα ή ελάχιστα.Το θέμα έχει εξαντληθεί και απαντηθεί δεόντως.
Θωμάς
Η γνώση μας κάνει περήφανους, η σοφία ταπεινούς.
- Α.Κυριακόπουλος
- Δημοσιεύσεις: 988
- Εγγραφή: Κυρ Ιαν 04, 2009 9:49 am
- Τοποθεσία: ΧΟΛΑΡΓΟΣ
Re: Λύσεις Μαθ. κατ. 2009
Αγαπητέ Λεωνίδα.iosifile έγραψε:Αγαπητοί συνάδελφοι,
Με αφορμή το εξής σχόλιο του κ. Α.Κυριακόπουλου :
«3) Γράφεις: « Ανεξάρτητα αν είναι δυνατόν ή όχι να βρούμε δύο διαφορετικές τιμές του α, πρέπει να υπάρξει αιτιολόγηση. Αυτό λέει ο Λεωνίδας». Θα μου επιτρέψεις να σου πω ότι αυτό ακριβώς είναι το λάθος του Λεωνίδα. Τι να αιτιολογήσουμε; Αφού αποδείξαμε αυτό που μας ζητούσαν δεν τελειώσαμε; Οτιδήποτε άλλο προσθέσουμε, όχι μόνο θα είναι λάθος, αλλά θα δείχνει ότι δεν έχουμε κατανοήσει την έννοια της απόδειξης στα μαθηματικά.»
Θέλω να δείτε τις εξής ασκήσεις:
ΑΣΚΗΣΗ 1:
Δίνεται η συνάρτηση
f(x)=α^x - ln(x+1) , x>-1
Αν η f(x) παρουσιάζει τοπικό ακρότατο στο 0, να αποδείξετε ότι α=e.
ΑΣΚΗΣΗ 2:
Δίνεται η συνάρτηση
f(x)= α^x - ln(x+1) , x>-1
Αν η f(x) παρουσιάζει τοπικό ελάχιστο στο 0, να αποδείξετε ότι α=e.
ΑΣΚΗΣΗ 3
Δίνεται η συνάρτηση
f(x)= α^x - ln(x+1) , x>-1
Αν η f(x) παρουσιάζει ολικό ελάχιστο στο 0, να αποδείξετε ότι α=e.
Οι τρεις αυτές ασκήσεις είναι εντελώς διαφορετικές ωστόσο λύνονται με τον ίδιο τρόπο!!!
Ξεκινάμε λέγοντας ότι πρέπει f΄(0)=0=> … =>α=e.
Δηλαδή, αγαπητοί συνάδελφοι είτε λέμε ότι η f παρουσιάζει τοπικό ακρότατο, είτε τοπικό ελάχιστο, είτε ολικό ελάχιστο η αποδεικτική διαδικασία είναι ακριβώς η ίδια!!! Μα καλά, 3 διαφορετικές ασκήσεις, λύνονται με τον ίδιο ακριβώς τρόπο; Το γεγονός ότι η άσκηση 2 έχει ένα παραπάνω δεδομένο από την 1 δεν επηρεάζει τη λύση ; Όμοια και για τις ασκήσεις 2 και 3. Δεν είναι αυτό περίεργο; Χρησιμοποιήθηκαν όλα τα δεδομένα μας πλήρως στις λύσεις αυτές για τις ασκήσεις 2 και 3;
Για αυτό το λόγο διαφωνώ πλήρως με αυτά που είπε ο συνάδελφος. Το ίδιο συμβαίνει και με την άσκηση 3 Α. Αν η άσκηση έδινε τοπικό ακρότατο στο 0 τι θα άλλαζε στην απόδειξη; ΤΙΠΟΤΑ. Άρα η λύση του 3 Α σίγουρα δεν τελειώνει εδώ.
Φιλικά
Λ. Ιωσηφίδης
Που είναι το περίεργο στο ότι και οι τρεις ασκήσεις που αναφέρεις λύνονται με τον ίδιο ακριβώς τρόπο; Μήπως ξεχνάς ότι στις υποθέσεις του θεωρήματος του Fermat είναι ότι η συνάρτηση παρουσιάζει( σε ένα εσωτερικό σημείο του συνόλου ορισμού της) τοπικό ακρότατο και δεν έχει καμία σημασία αν αυτό είναι: τοπικό ελάχιστο ή τοπικό μέγιστο ή ολικό ελάχιστο ή ολικό μέγιστο; Και στις τρεις ασκήσεις που αναφέρεις ( όπως και σε κάθε άλλη άσκηση) όταν αποδείξουμε αυτό που μας ζητάνε βάζουμε τελεία και η απόδειξη έχει τελειώσει (Ο.Ε.Δ. Κουράστηκα να το γράφω).
Αγαπητέ Λεωνίδα. Διαφώνησε μαζί μου όσο θέλεις. Θα σε παρακαλούσα όμως να το ξανασκεφτείς και να διαβάσεις προσεκτικά τα προηγούμενα μηνύματά μου, όπως και των άλλων συναδέλφων.
Θα μου ήταν πολύ δυσάρεστο αν αναγκαζόμουνα να επανέλθω στο ίδιο θέμα.
Με εκτίμηση
Αντώνης Κυριακόπουλος
•Ο έξυπνος παραδέχεται •Ο πονηρός δικαιολογείται •Ο βλάκας επιμένει
•Ο έξυπνος παραδέχεται •Ο πονηρός δικαιολογείται •Ο βλάκας επιμένει
- Κοτρώνης Αναστάσιος
- Επιμελητής
- Δημοσιεύσεις: 3203
- Εγγραφή: Κυρ Φεβ 22, 2009 11:11 pm
- Τοποθεσία: Μπροστά στο πισί...
- Επικοινωνία:
Re: Λύσεις Μαθ. κατ. 2009
Εδώ κατα τη γνώμη μου υπάρχει ένα ζήτημα.Α.Κυριακόπουλος έγραψε: όταν αποδείξουμε αυτό που μας ζητάνε βάζουμε τελεία και η απόδειξη έχει τελειώσει
Παραπέμπω στη συζήτηση
viewtopic.php?f=55&t=1021&hilit=%CE%9C% ... E%BE%CE%B7
στο σχόλιο του gatou για το θέμα των πανελληνίων του 97 όπου συνάρτηση με τις δοθείσες ιδιότητες δεν υπήρχε, με αποτέλεσμα, υποθέτοντας κανείς την ύπαρξή της να μπορεί να αποδείξει "τα πάντα", ακόμα και ότι e=1
(όπως παρατήρησε ο gatos). Θα μπορούσε βέβαια κανείς να περιοριστεί στο να αποδείξει, όπως του ζητήθηκε, την αλήθεια της συνεπαγωγής : ύπαρξη τέθοιας f
 κάτι.. . Κάτα πόσο όμως έχει νόημα ένα τέθοιο θέμα;
κάτι.. . Κάτα πόσο όμως έχει νόημα ένα τέθοιο θέμα;Αν για παράδειγμα κάποιος μαθητής από περιέργεια επεξεργαζόταν λίγο παραπάνω τις δοθείσες σχέσεις και κατέληγε στο ότι e=1, δε θα αντιμετώπιζε τραγικό πρόβλημα;
Εσύ....; Θα γίνεις κανίβαλος....;
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3342
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Λύσεις Μαθ. κατ. 2009
Ελεγα καποτε στους φοιτητες μου "question your answers!" ("να αμφισβητειτε τις απαντησεις σας!"), τωρα οδηγουμαστε στο "question our questions!" ("να αμφισβητειτε τις ερωτησεις μας!") 
Γιωργος Μπαλογλου
Γιωργος Μπαλογλου
Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
-
k-ser
- Δημοσιεύσεις: 870
- Εγγραφή: Σάβ Δεκ 20, 2008 10:22 am
- Τοποθεσία: Μουζάκι Καρδίτσας
- Επικοινωνία:
Re: Λύσεις Μαθ. κατ. 2009
Αναστάση,Κοτρώνης Αναστάσιος έγραψε: Εδώ κατα τη γνώμη μου υπάρχει ένα ζήτημα.
Παραπέμπω στη συζήτηση
viewtopic.php?f=55&t=1021&hilit=%CE%9C% ... E%BE%CE%B7
στο σχόλιο του gatou για το θέμα των πανελληνίων του 97 όπου συνάρτηση με τις δοθείσες ιδιότητες δεν υπήρχε, με αποτέλεσμα, υποθέτοντας κανείς την ύπαρξή της να μπορεί να αποδείξει "τα πάντα", ακόμα και ότι e=1
(όπως παρατήρησε ο gatos). Θα μπορούσε βέβαια κανείς να περιοριστεί στο να αποδείξει, όπως του ζητήθηκε, την αλήθεια της συνεπαγωγής : ύπαρξη τέτοιας fκάτι.. . Κάτα πόσο όμως έχει νόημα ένα τέθοιο θέμα;
Αν για παράδειγμα κάποιος μαθητής από περιέργεια επεξεργαζόταν λίγο παραπάνω τις δοθείσες σχέσεις και κατέληγε στο ότι e=1, δε θα αντιμετώπιζε τραγικό πρόβλημα;
και βέβαια έχει νόημα ένα τέτοιο θέμα. Εξάλλου, αποτελεί τη βάση της "εις άτοπο απαγωγής".
Υποθέτω ότι κάποια ψευδής πρόταση είναι αληθής και συμπεραίνω μία ψευδή μαθηματική πρόταση.
Στη συζήτηση που αναφέρεις, γράφω ότι, ένα τέτοιο θέμα, δεν είναι καλό να δίνεται - δεν είναι μαθηματικά ορθό, με την εξής έννοια:
δοσμένης μιας ψευδής υπόθεσης μπορούμε να αποδείξουμε, όπως γράφεις, τα πάντα - κάθε αληθή ή ψευδή μαθηματική πρόταση.
Κώστας Σερίφης
- Κοτρώνης Αναστάσιος
- Επιμελητής
- Δημοσιεύσεις: 3203
- Εγγραφή: Κυρ Φεβ 22, 2009 11:11 pm
- Τοποθεσία: Μπροστά στο πισί...
- Επικοινωνία:
Re: Λύσεις Μαθ. κατ. 2009
Μεβάση το παραπάνω το θέμα θα έπρεπε να είχε τεθεί υπό τη διατύπωση : Δείξτε ότι δεν υπάρχει συνάρτηση με τις τάδε ιδιότητες.k-ser έγραψε:και βέβαια έχει νόημα ένα τέτοιο θέμα. Εξάλλου, αποτελεί τη βάση της "εις άτοπο απαγωγής".
Σαφώς όμως και δεν τέθηκε έτσι γιατί οι θεματοδότες δεν είχαν προφανώς καν υπόψιν την μη ύπαρξη μιας τέθοιας συνάρτησης.
Εκεί είναι που αρχίζουν να δημιουργούνται τα προβλήματα....
Εσύ....; Θα γίνεις κανίβαλος....;
-
k-ser
- Δημοσιεύσεις: 870
- Εγγραφή: Σάβ Δεκ 20, 2008 10:22 am
- Τοποθεσία: Μουζάκι Καρδίτσας
- Επικοινωνία:
Re: Λύσεις Μαθ. κατ. 2009
Αναστάση,
ρωτάς: έχει νόημα να τεθεί σαν πρόβλημα προς απόδειξη μια συνεπαγωγή με ψευδή πρόταση την Α;
με ψευδή πρόταση την Α;
Η απάντησή μου είναι: Ναι.
Αιτιολογώ την απάντησή μου λέγοντάς σου ότι την παραπάνω διαδικασία την εφαρμόζουμε στην απόδειξη με τη μέθοδο της εις "άτοπον απαγωγής".
Δηλαδή, αν δεν είχε νόημα να τεθεί ένα τέτοιο πρόβλημα, δεν θα είχε νόημα και η μέθοδος της εις "άτοπον απαγωγής".
Η απάντησή μου δεν ήταν: Ναι, εφόσον το θέμα τίθεται για να αποδείξουμε την μη αλήθεια της υπόθεσης με τη μέθοδο της εις "άτοπο επαγωγής"!
Φιλικά
ρωτάς: έχει νόημα να τεθεί σαν πρόβλημα προς απόδειξη μια συνεπαγωγή
 με ψευδή πρόταση την Α;
με ψευδή πρόταση την Α;Η απάντησή μου είναι: Ναι.
Αιτιολογώ την απάντησή μου λέγοντάς σου ότι την παραπάνω διαδικασία την εφαρμόζουμε στην απόδειξη με τη μέθοδο της εις "άτοπον απαγωγής".
Δηλαδή, αν δεν είχε νόημα να τεθεί ένα τέτοιο πρόβλημα, δεν θα είχε νόημα και η μέθοδος της εις "άτοπον απαγωγής".
Η απάντησή μου δεν ήταν: Ναι, εφόσον το θέμα τίθεται για να αποδείξουμε την μη αλήθεια της υπόθεσης με τη μέθοδο της εις "άτοπο επαγωγής"!
Φιλικά
Κώστας Σερίφης
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες
