Καλησπέρα παιδιά. θα ήθελα να με βοηθήσετε σχετικά με το που κυμαίνομαι στην βαθμολογία
Καταρχάς στο β3 βρήκα μόνο την ασύμπτωτη στο μείον άπειρο λέγοντας οτι η ευθεία

είναι η μοναδική ασύμπωτη. Δεν έδειξα οτι ειναι και στο σύν άπειρο επειδή η διαδικασία είναι ίδια.
Στο γ2 έθεσα συναρτηση

εδειξα οτι δν μηδενίζεται για

και οτι διατηρεί σταθ πρόσημο. Οπότε για

ο τύπος είναι όπως αυτός στο γ1 ερώτημα και έκανα το ιδιο για

οπότε έβγαλα τον ίδιο τύπο ξανά.
στο γ4 πήρα την βασικη σχέση

και επειδή δουλέυω για

έβγαλα το απόλυτο απ το δεύτερο μέλος και μετά πέρασα μονοτονία της

για να δημιουργήσω τις σχέσεις που μου δίνει. Το ίδιο έκανα και για το
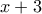
οπότε έφτιαξα 2 ανισώσεις. Μετά όμως τ λαθος είναι οτι τις αφαίρεσα και είπα οτι η ισότητα ισχύει για

και επειδή

γνησίως αύξουσα θα είναι μοναδική.
Στο Δ1 το

το βρήκα κάνοντας delhopital στο όριο που μου δίνεται σαν δεδομένο επειδή

2 φορές παρ/μη και συνεχής. Είναι σωστό;
Τέλος στο Δ4 είπα

πέρασα
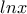
μονοτονία της

μετά ολοκλήρωμα και το βρήκα . Θα χάσω κατι;
Θα ήθελα να μου πείτε απο τα παραπάνω πόσα μόρια χάνω στην χειρότερη περίπτωση
είναι κυρτή. Άρα δεν υπάρχουν παράλληλες εφαπτομένες σε οποιαδήποτε σημεία, σωστά ;
(σε οποιαδήποτε διαστήματα), τέτοια ώστε
με
διαφορετικό του
.
 που παίρνεις είναι διαφορετικά αν τα διαστήματα είναι οποιαδήποτε; (Αν τα διαστήματα αλληλοεπικαλύπτονται μπορεί τα
που παίρνεις είναι διαφορετικά αν τα διαστήματα είναι οποιαδήποτε; (Αν τα διαστήματα αλληλοεπικαλύπτονται μπορεί τα  να ταυτίζονται κάτι που ΔΕ θέλεις για να μπορείς να καταλήξεις σε άτοπο).
να ταυτίζονται κάτι που ΔΕ θέλεις για να μπορείς να καταλήξεις σε άτοπο).
 είναι η μοναδική ασύμπωτη. Δεν έδειξα οτι ειναι και στο σύν άπειρο επειδή η διαδικασία είναι ίδια.
είναι η μοναδική ασύμπωτη. Δεν έδειξα οτι ειναι και στο σύν άπειρο επειδή η διαδικασία είναι ίδια. εδειξα οτι δν μηδενίζεται για
εδειξα οτι δν μηδενίζεται για  και οτι διατηρεί σταθ πρόσημο. Οπότε για
και οτι διατηρεί σταθ πρόσημο. Οπότε για ο τύπος είναι όπως αυτός στο γ1 ερώτημα και έκανα το ιδιο για
ο τύπος είναι όπως αυτός στο γ1 ερώτημα και έκανα το ιδιο για  οπότε έβγαλα τον ίδιο τύπο ξανά.
οπότε έβγαλα τον ίδιο τύπο ξανά. και επειδή δουλέυω για
και επειδή δουλέυω για 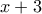 οπότε έφτιαξα 2 ανισώσεις. Μετά όμως τ λαθος είναι οτι τις αφαίρεσα και είπα οτι η ισότητα ισχύει για
οπότε έφτιαξα 2 ανισώσεις. Μετά όμως τ λαθος είναι οτι τις αφαίρεσα και είπα οτι η ισότητα ισχύει για  και επειδή
και επειδή  το βρήκα κάνοντας delhopital στο όριο που μου δίνεται σαν δεδομένο επειδή
το βρήκα κάνοντας delhopital στο όριο που μου δίνεται σαν δεδομένο επειδή  πέρασα
πέρασα 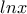 μονοτονία της
μονοτονία της ![f((- \infty,0])=(- \infty,0] f((- \infty,0])=(- \infty,0]](/forum/ext/geomar/texintegr/latexrender/pictures/deb4697ad4417422d088a33e2ffc6a21.png) , αυτό είναι εύκολο. Σε εκείνο ειδικώς το διάστημα έχει βεβαίως αντίστροφη
, αυτό είναι εύκολο. Σε εκείνο ειδικώς το διάστημα έχει βεβαίως αντίστροφη  , με
, με ![f^{-1}(- \infty , 0] =(- \infty , 0] f^{-1}(- \infty , 0] =(- \infty , 0]](/forum/ext/geomar/texintegr/latexrender/pictures/7b57d5d3c960f98f4b5df9266ae56cc9.png)
 και θέσουμε όπου
και θέσουμε όπου  το
το  θα πάρουμε την :
θα πάρουμε την : .
. που μετατρέπεται στην
που μετατρέπεται στην  και θεωρώντας της
και θεωρώντας της  στο
στο ![(- \infty,0] (- \infty,0]](/forum/ext/geomar/texintegr/latexrender/pictures/eb9318020aa8e809ad430e1e3559edd3.png) η οποία είναι γνησίως αύξουσα ως άθροισμα των γνησίως αυξουσών συναρτήσεων
η οποία είναι γνησίως αύξουσα ως άθροισμα των γνησίως αυξουσών συναρτήσεων  .
. , στο
, στο  και τη σχέση που ισχύει
και τη σχέση που ισχύει  (1).
(1). , τότε
, τότε  για
για  άρα είναι γνήσια φθίνουσα στο διάστημα
άρα είναι γνήσια φθίνουσα στο διάστημα ![(-\propto ,0] (-\propto ,0]](/forum/ext/geomar/texintegr/latexrender/pictures/2270d36a09b2b2c717f9085ed9630bf3.png) .
. , τότε
, τότε  ,
, 
 άτοπο.
άτοπο. , τότε
, τότε  ,
, 
 άτοπο.
άτοπο. .
. . Επειδή ο χρόνος αυτές τις μέρες είναι περιορισμένος και το μυαλό πολύ ταλαιπωρημένο, παρακαλώ τους συναδέλφους να ελέγξουν τις παραπάνω σκέψεις. Αν δεν έχουν κάποιο λάθος, θα το ξανακοιτάξω μήπως καταφέρω να το συμπληρώσω όταν βρω χρόνο!
. Επειδή ο χρόνος αυτές τις μέρες είναι περιορισμένος και το μυαλό πολύ ταλαιπωρημένο, παρακαλώ τους συναδέλφους να ελέγξουν τις παραπάνω σκέψεις. Αν δεν έχουν κάποιο λάθος, θα το ξανακοιτάξω μήπως καταφέρω να το συμπληρώσω όταν βρω χρόνο! στην προηγούμενη σελίδα οι οποίοι είναι εξίσου μία χαρά!
στην προηγούμενη σελίδα οι οποίοι είναι εξίσου μία χαρά!  είναι μοναδική λύση της εξίσωσης.
είναι μοναδική λύση της εξίσωσης.  που να είναι λύση της εξίσωσης. Ισxύει
που να είναι λύση της εξίσωσης. Ισxύει 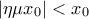 (από τη γνωστή ανισότητα
(από τη γνωστή ανισότητα  με ισότητα μόνο για
με ισότητα μόνο για  και
και 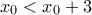 .
. Αν
Αν 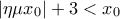 τότε
τότε  και επειδή ισxύουν οι προϋποθέσεις του ΘΜΤ σε κάθε ένα από τα διαστήματα
και επειδή ισxύουν οι προϋποθέσεις του ΘΜΤ σε κάθε ένα από τα διαστήματα ![\left[|\eta\mu x_0|, |\eta\mu x_0|+3\right], \ \left[x_0,x_0+3\right] \left[|\eta\mu x_0|, |\eta\mu x_0|+3\right], \ \left[x_0,x_0+3\right]](/forum/ext/geomar/texintegr/latexrender/pictures/b23bf28fb8af84eff9d273f63a43f50a.png) άρα υπάρxουν
άρα υπάρxουν  ώστε η εξίσωση να γράφεται:
ώστε η εξίσωση να γράφεται: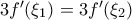 απ΄όπου
απ΄όπου  και αφού η
και αφού η  είναι γνησίως αύξουσα (ως κυρτή) άρα είναι και
είναι γνησίως αύξουσα (ως κυρτή) άρα είναι και  κι έτσι παίρνουμε
κι έτσι παίρνουμε  , πράγμα άτοπο αφού τα
, πράγμα άτοπο αφού τα 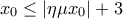 τότε
τότε 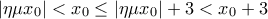 .
. 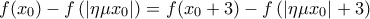
![\left[|\eta\mu x_0|, x_0\right], \ \left[|\eta\mu x_0|+3, x_0+3\right] \left[|\eta\mu x_0|, x_0\right], \ \left[|\eta\mu x_0|+3, x_0+3\right]](/forum/ext/geomar/texintegr/latexrender/pictures/35f56cb0e89ae84a5e44c3c79d576874.png) άρα υπάρxουν
άρα υπάρxουν  ώστε η εξίσωση να γράφεται:
ώστε η εξίσωση να γράφεται: και αφού
και αφού  άρα
άρα 
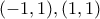 και ασύμπτωτη την
και ασύμπτωτη την  . Και έτσι όμως δεν είναι άσχημα,μια και δεν έχουμε πολύ δύσκολα νούμερα.
. Και έτσι όμως δεν είναι άσχημα,μια και δεν έχουμε πολύ δύσκολα νούμερα.