Αγαπητοί Μιχάλη Λάμπρου και Δημήτρη Σκουτέρη,dement έγραψε:Η γεωμετρία δεν ήταν δική μου, αλλά εν πάση περιπτώσει. Επειδή δεν φαίνεσαι να προβάλλεις ένσταση στηνΠαντελής Μιντεκίδης έγραψε: Μιχάλη Λάμπρου και Δημήτρη Σκουτέρη,
Αφήστε τους "γεωμετρικούς" παρελκισμούς! Για τελευταία φορά σας παρακαλώ! Δώστε το έσχατο μέρος της απόδειξης, δηλαδή: sinα+α<π, ώστε να ολοκληρώσετε την φυσική και κομψή σας απόδειξη!!!
Παντελής Μιντεκίδης, (που χρησιμοποιείται στο πρώτο τεταρτημόριο), υποθέτω ότι τη θεωρείς δεδομένη.
Λοιπόν (για δεύτερη φορά, δεν θα υπάρξει τρίτη).
Επιτέλους, μετά από 24 ώρες, ολοκληρώσατε (διά της εκμαιευτικής μεθόδου ...) την φυσική και κομψή σας απόδειξη (ερώτημα Γ1, 2017), έναντι της αφύσικης και άκομψης δικής μου που διδάσκεται κατά κόρον στο σχολικό βιβλίο και την γνωρίζουν όλοι οι καθηγητές και οι μαθητές, πέραν του γεγονότος ότι μαζί με την μονοτονία εφαρμόζεται για "όλες" τις συναρτήσεις, όταν θέλουμε να αποδείξουμε προτάσεις ύπαρξης "το πολύ ν λύσεων".
Πρέπει να γίνει κατανοητό ότι ουδόλως υποτιμώ την απόπειρα της γεωμετρικής σας λύσης, και αν επέμενα είναι διότι θέλω να βλέπω όντως λύσεις, τεκμηριωμένες.
Ευχαριστώ για την φιλοξενία των λύσεών μου, γεγονός που το mathematica.gr πράττει κάθε χρόνο, καθώς και για την εποικοδομητική συζήτηση,
Θερμούς χαιρετισμούς,
Παντελής Μιντεκίδης

 το πρωί έχω αεροπορικό ταξίδι και θα λείπω όλη μέρα. Δύσκολα θα μπορέσω να διαβάσω σχόλια, αν υπάρξουν. Ευελπιστώ ότι δεν θα υπάρξουν. Όποιος διαβάσει νηφάλια τα γραφόμενα, θα καταλάβει την απόδειξη που παραθέτω αν και ομολογώ ότι δεν βλέπω γιατί πρέπει να εξηγήσω τα ήδη γραμμένα. Ας είναι.
το πρωί έχω αεροπορικό ταξίδι και θα λείπω όλη μέρα. Δύσκολα θα μπορέσω να διαβάσω σχόλια, αν υπάρξουν. Ευελπιστώ ότι δεν θα υπάρξουν. Όποιος διαβάσει νηφάλια τα γραφόμενα, θα καταλάβει την απόδειξη που παραθέτω αν και ομολογώ ότι δεν βλέπω γιατί πρέπει να εξηγήσω τα ήδη γραμμένα. Ας είναι. πέρα από αυτές στα
πέρα από αυτές στα  , έστω
, έστω  . Η εφαπτομένη στο
. Η εφαπτομένη στο 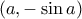 έχει κλίση
έχει κλίση  . Επίσης θα έπρεπε να έχει κλίση
. Επίσης θα έπρεπε να έχει κλίση  , που αντιβαίνει στην
, που αντιβαίνει στην  .
.  ή, εργαζόμαστε με την συμμετρία που έχουμε ως προς τον άξονα
ή, εργαζόμαστε με την συμμετρία που έχουμε ως προς τον άξονα  ". Ας δούμε τις λεπτομέριεις παρ' όλο ότι είναι τετριμμένη παραλλαγή του παραπάνω.
". Ας δούμε τις λεπτομέριεις παρ' όλο ότι είναι τετριμμένη παραλλαγή του παραπάνω. είναι άμεση (οριζόντια εφαπτομένη). Μένει η περίπτωση
είναι άμεση (οριζόντια εφαπτομένη). Μένει η περίπτωση 
 στην θέση του
στην θέση του  . Κάνω άλλη παραλλαγή για λόγους πολυφωνίας. Ομολογώ ότι δεν βλέπω γιατί δεν έγινε κατανοητή την πρώτη φορά, στο σημείο που επικαλέστηκα την συμμετρία του σχήματος, αλλά ας είναι. Ας κάνω και τα προφανή αφού δυσκολεύουν κάποιους.
. Κάνω άλλη παραλλαγή για λόγους πολυφωνίας. Ομολογώ ότι δεν βλέπω γιατί δεν έγινε κατανοητή την πρώτη φορά, στο σημείο που επικαλέστηκα την συμμετρία του σχήματος, αλλά ας είναι. Ας κάνω και τα προφανή αφού δυσκολεύουν κάποιους.  , που διέρχεται από το
, που διέρχεται από το 

 και η προηγούμενη γράφεται
και η προηγούμενη γράφεται  (άμεσο)
(άμεσο) .
.