Γεια σου Σταύρο,ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τετ Ιουν 17, 2020 10:47 pmΓεια σου Γιώργο.george visvikis έγραψε: ↑Τετ Ιουν 17, 2020 10:27 pmΠοτέ δεν αναφέρθηκα στο σχήμα. Προσπαθώ να καταλάβω τι γίνεται. Έχουμε ένα ισοσκελές τρίγωνοΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τετ Ιουν 17, 2020 7:19 pmΕξαρτάται πως θα το πάρεις.george visvikis έγραψε: ↑Τετ Ιουν 17, 2020 7:08 pmΚι όμως Σταύρο, η ουσία αλλάζει. Δεν έπρεπε να δοθείγιατί
και έτσι ακυρώνονται τα ερωτήματα (Γ.3), (Γ.4).
Για κανονικά μαθηματικά αν δοθεί σχήμα αυτό είναι βοηθητικό.
Δηλαδή σου κάνει το σχήμα για μια περίπτωση.
Ετσι η άσκηση δεν έχει πρόβλημα γιατί ο τύπος
του εμβαδού δεν αλλάζει αν η γωνία είναι αμβλεία.
Τώρα για σχολικά μαθηματικά θα μου επιτρέψεις να μην
εκφέρω γνώμη.
Είναι άλλοι πιο ειδικοί από εμένα.π.χ εσύ.τη διάμεσό του
το περίκεντρο
και
Στα κανονικά μαθηματικά η γωνία
μπορεί να είναι αμβλεία;
Τι λέω εγώ.
Λέω ότι η
δεν είναι σωστό.
Το έχει σημειώσει στο σχήμα το οποίο το έχει κάνει όταν η γωνία είναι οξεία.
Εσύ από ότι καταλαβαίνω (διόρθωσε με αν κάνω λάθος)
λες ότι αφού στο σχήμα το έχει βάλει έτσι, έτσι θα είναι.
Και σε σχολικό επίπεδο έχεις και δίκιο.
Συνήθως στα Μαθηματικά τα σχήματα απέχουν πάρα πολύ από την πραγματικότητα.
π.χ σχεδιάζουμε σχήματα σε χώρους άπειρης διάστασης.
σχεδιάζουμε τρίγωνα με άθροισμα γωνιών μικρότερο του
(στην Υπερβολική Γεωμετρία)
Το ζήτημα είναι τι είναι σχήμα.
Τώρα για το σχολείο δεν ξέρω τι κανόνες ισχύουν.
Σε τελική ανάλυση δεν νομίζω ότι διαφωνούμε.
Τελικά υπάρχει παρεξήγηση. Εσύ νομίζεις ότι το είδα στο σχήμα, αλλά εγώ αναφέρομαι στην εκφώνηση. Δεν έλαβα υπόψη μου το σχήμα. Στην εκφώνηση όμως αναφέρεται ρητά ότι



 στον υπολογισμό του ζητούμενου ορίου, τους οδήγησε στη σκέψη να σχηματίσουν μέσα στο όριο τον λόγο μεταβολής
στον υπολογισμό του ζητούμενου ορίου, τους οδήγησε στη σκέψη να σχηματίσουν μέσα στο όριο τον λόγο μεταβολής  που οδηγεί στον ορισμό της παραγώγου.
που οδηγεί στον ορισμό της παραγώγου.![\mathop {\lim }\limits_{x \to x_0 } \frac{1}{{x - x_0 }}[\frac{{x - x_0 }}{{f(x) - f(x_0 )}} + (x - x_0 )\eta \mu \frac{1}{{x - x_0 }}] = \mathop {\lim }\limits_{x \to x_0 } \frac{1}{{x - x_0 }}[\frac{{x - x_0 }}{{f(x) - f(x_0 )}} + (x - x_0 )\eta \mu \frac{1}{{x - x_0 }}] =](/forum/ext/geomar/texintegr/latexrender/pictures/bb7ae9c664d5f33b00a9af5c249e7f60.png)
![= \mathop {\lim }\limits_{x \to x_0 } \frac{1}{{x - x_0 }}[\frac{1}{{\frac{{f(x) - f(x_0 )}}{{x - x_0 }}}} + (x - x_0 )\eta \mu \frac{1}{{x - x_0 }}] = \mathop {\lim }\limits_{x \to x_0 } \frac{1}{{x - x_0 }}[\frac{1}{{\frac{{f(x) - f(x_0 )}}{{x - x_0 }}}} + (x - x_0 )\eta \mu \frac{1}{{x - x_0 }}]](/forum/ext/geomar/texintegr/latexrender/pictures/b0d6a4dee106518b5a7619b95f86475d.png)
 (μηδενική επί φραγμένη)
(μηδενική επί φραγμένη)

 τότε:
τότε: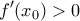 άρα
άρα 

 είναι
είναι 
 τότε
τότε άρα
άρα 

 είναι
είναι 

 έχουμε
έχουμε  άρα
άρα  άρα
άρα 
 , εγγεγραμένο σε κύκλο ακτίνας 1. Αν
, εγγεγραμένο σε κύκλο ακτίνας 1. Αν  και
και  , να βρεθεί το εμβαδό του τριγώνου συναρτήσει του θ")
, να βρεθεί το εμβαδό του τριγώνου συναρτήσει του θ") αφού το θ είναι γωνία τριγώνου.
αφού το θ είναι γωνία τριγώνου. :
:


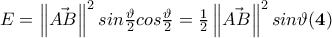



 οδηγεί στο συμπέρασμα ότι
οδηγεί στο συμπέρασμα ότι  , αφού για
, αφού για  το εγγεγραμένο τρίγωνο βαίνει σε ημικύκλιο οπότε τα σημεία Ο και Μ ταυτίζονται, ενώ για
το εγγεγραμένο τρίγωνο βαίνει σε ημικύκλιο οπότε τα σημεία Ο και Μ ταυτίζονται, ενώ για  η γωνία
η γωνία 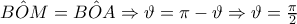
 σε κύκλο ακτίνας
σε κύκλο ακτίνας  ισούται προς
ισούται προς  ... κλπ κλπ]
... κλπ κλπ]

 με
με





 εχουμε
εχουμε  μιγαδικό και τα
μιγαδικό και τα  είναι μιγαδικοί
είναι μιγαδικοί 


 στην εκφώνηση, αρκούσε να την δείξουν στο σχήμα ... είτε αναμένοντας τους διαγωνιζόμενους και διαγωνιζόμενες να επεκτείνουν στην περίπτωση της αμβλείας γωνίας είτε όχι
στην εκφώνηση, αρκούσε να την δείξουν στο σχήμα ... είτε αναμένοντας τους διαγωνιζόμενους και διαγωνιζόμενες να επεκτείνουν στην περίπτωση της αμβλείας γωνίας είτε όχι  και στο
και στο  , το λεγόμενο απόστημα, τότε το εμβαδόν του ισοσκελούς τριγώνου ισούται προς
, το λεγόμενο απόστημα, τότε το εμβαδόν του ισοσκελούς τριγώνου ισούται προς  , όπου
, όπου  -- θετικό
-- θετικό 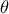 ), αρνητικό
), αρνητικό  και από το Δ3 , το
και από το Δ3 , το  .
.![[x_{0} , \rho ] [x_{0} , \rho ]](/forum/ext/geomar/texintegr/latexrender/pictures/f90249e8cdf6609a718b72a5bd0fc6ca.png) , δίνει την κλίση της εφαπτομένης στο σημείο
, δίνει την κλίση της εφαπτομένης στο σημείο  .
. είναι γνησίως αύξουσα , προκύπτει η :
είναι γνησίως αύξουσα , προκύπτει η :  .
. , με το
, με το  και λίγες πράξεις δίνουν το ζητούμενο .
και λίγες πράξεις δίνουν το ζητούμενο . είναι συνεχής και παραγωγίσιμη στο
είναι συνεχής και παραγωγίσιμη στο  ως άθροισμα τέτοιων συναρτήσεων με
ως άθροισμα τέτοιων συναρτήσεων με  .
.  για κάθε
για κάθε  , γεγονός που αποδεικνύει ότι η
, γεγονός που αποδεικνύει ότι η  είναι
είναι ![\left[0,1\right] \left[0,1\right]](/forum/ext/geomar/texintegr/latexrender/pictures/4f27db35c23e1b587a92f6ba055a4b94.png) και του γεγονότος ότι
και του γεγονότος ότι , έπεται από το Θεώρημα του Bolzano ότι υπάρχει
, έπεται από το Θεώρημα του Bolzano ότι υπάρχει  ώστε
ώστε  ,
,  και
και  , δηλαδή
, δηλαδή ![\left(-\infty,x_0\right] \left(-\infty,x_0\right]](/forum/ext/geomar/texintegr/latexrender/pictures/d16355589a3254877943b479c68859e0.png) , γνησίως αύξουσα στο
, γνησίως αύξουσα στο  , δηλαδή
, δηλαδή  για κάθε
για κάθε  , οπότε
, οπότε  .
. έχουμε
έχουμε  , οπότε
, οπότε 
 , και επιπλέον
, και επιπλέον  , έπεται ότι
, έπεται ότι  και από το κριτήριο παρεμβολής
και από το κριτήριο παρεμβολής![\lim_{x\to x_0}\left[\dfrac{1}{f(x)-f(x_0)}+\eta \mu\,\left(\dfrac{1}{x-x_0}\right)\right]=+\infty \lim_{x\to x_0}\left[\dfrac{1}{f(x)-f(x_0)}+\eta \mu\,\left(\dfrac{1}{x-x_0}\right)\right]=+\infty](/forum/ext/geomar/texintegr/latexrender/pictures/837803048193cbdc74cf3becdb9c36fa.png)
![h(x)=f(x)+x-x_0\,,x\in\left[x_0,1\right] h(x)=f(x)+x-x_0\,,x\in\left[x_0,1\right]](/forum/ext/geomar/texintegr/latexrender/pictures/a6be59a37e95fe27e297bf2a2fd45baa.png) είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο ![\left[x_0,1\right] \left[x_0,1\right]](/forum/ext/geomar/texintegr/latexrender/pictures/8f16cda250af5ec7ad477b89468ac3d0.png) ως άθροισμα της γνησίως αύξουσας
ως άθροισμα της γνησίως αύξουσας![x\mapsto x-x_0\,,x\in\left[x_0,1\right] x\mapsto x-x_0\,,x\in\left[x_0,1\right]](/forum/ext/geomar/texintegr/latexrender/pictures/eb5048063f1a487a353fe30202db4a18.png) . Επίσης, είναι συνεχής ώς άθροισμα συνεχών με
. Επίσης, είναι συνεχής ώς άθροισμα συνεχών με  διότι
διότι  και
και  , οπότε από μονοτονία και Θεώρημα Bolzano, υπάρχει
, οπότε από μονοτονία και Θεώρημα Bolzano, υπάρχει ώστε
ώστε  .
. . Η
. Η ![\left[x_0,\rho\right] \left[x_0,\rho\right]](/forum/ext/geomar/texintegr/latexrender/pictures/ba622b0fb9888e5f2889ac481cc0eceb.png) , οπότε υπάρχει
, οπότε υπάρχει ώστε
ώστε  .
. και η
και η 
 .
. , η πεπλατυσμένη ευθεία των πραγματικών.
, η πεπλατυσμένη ευθεία των πραγματικών.
 στο οποίο η f παρουσιάζει ολικό ελάχιστο και
στο οποίο η f παρουσιάζει ολικό ελάχιστο και
![\displaystyle \underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\ \left[ \frac{1}{f\left( x \right)-f\left( {{x}_{0}} \right)}+\frac{\eta \mu \left( \frac{1}{x-{{x}_{0}}} \right)}{x-{{x}_{0}}} \right]\ . \displaystyle \underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\ \left[ \frac{1}{f\left( x \right)-f\left( {{x}_{0}} \right)}+\frac{\eta \mu \left( \frac{1}{x-{{x}_{0}}} \right)}{x-{{x}_{0}}} \right]\ .](/forum/ext/geomar/texintegr/latexrender/pictures/9108622b3f3ae9b1d8b112ffd575936d.png)
 είναι το σημείο του ερωτήματος Δ1, να δείξετε ότι η εξίσωση
είναι το σημείο του ερωτήματος Δ1, να δείξετε ότι η εξίσωση  έχει στο
έχει στο 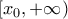 μοναδική ρίζα ρ, η οποία ανήκει στο
μοναδική ρίζα ρ, η οποία ανήκει στο 
 ώστε
ώστε 
 ισχύει
ισχύει  όπου
όπου 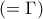 είναι εγγεγραμμένο σε κύκλο με κέντρο O και ακτίνα 1, όπως φαίνεται στο σχήμα (δίνεται ότι η ευθεία ΑΟ τέμνει την ΒΓ στο σημείο Μ). Αν
είναι εγγεγραμμένο σε κύκλο με κέντρο O και ακτίνα 1, όπως φαίνεται στο σχήμα (δίνεται ότι η ευθεία ΑΟ τέμνει την ΒΓ στο σημείο Μ). Αν  είναι η γωνία μεταξύ των ίσων πλευρών του τριγώνου και
είναι η γωνία μεταξύ των ίσων πλευρών του τριγώνου και 

 για την οποία το εμβαδόν του τριγώνου μεγιστοποιείται.
για την οποία το εμβαδόν του τριγώνου μεγιστοποιείται.  με
με  για τις οποίες το εμβαδόν του τριγώνου ισούται με
για τις οποίες το εμβαδόν του τριγώνου ισούται με 
 ,με
,με  τέτοια, ώστε:
τέτοια, ώστε: 
