Μαθηματικά προσανατολισμού 2022 (Θέματα & Λύσεις)
-
Επιτροπή Θεμάτων 2023
- Δημοσιεύσεις: 28
- Εγγραφή: Πέμ Μάιος 12, 2016 9:41 am
Μαθηματικά προσανατολισμού 2022 (Θέματα & Λύσεις)
Αγαπητές/τοί φίλες/οι
Στο θέμα αυτό θα αναρτηθούν (αμέσως μόλις δημοσιευθούν στη σελίδα του Υπουργείου) και, αποκλειστικά, θα λυθούν τα θέματα των Μαθηματικών προσανατολισμού 2022 (των ημερησίων ΓΕΛ). Επομένως σχολιασμοί-κριτική επί της δυσκολίας κ.λ.π. των θεμάτων θα απομακρύνονται από αυτήν την συζήτηση. Αυτές μπορούν να γίνουν στο Σχόλια στα Μαθηματικά προσανατολισμού 2022
Στο θέμα αυτό θα αναρτηθούν (αμέσως μόλις δημοσιευθούν στη σελίδα του Υπουργείου) και, αποκλειστικά, θα λυθούν τα θέματα των Μαθηματικών προσανατολισμού 2022 (των ημερησίων ΓΕΛ). Επομένως σχολιασμοί-κριτική επί της δυσκολίας κ.λ.π. των θεμάτων θα απομακρύνονται από αυτήν την συζήτηση. Αυτές μπορούν να γίνουν στο Σχόλια στα Μαθηματικά προσανατολισμού 2022
Λέξεις Κλειδιά:
- Πρωτοπαπάς Λευτέρης
- Συντονιστής
- Δημοσιεύσεις: 2937
- Εγγραφή: Τετ Οκτ 14, 2009 12:20 am
- Τοποθεσία: Πετρούπολη, Αθήνα
- Επικοινωνία:
Re: Μαθηματικά προσανατολισμού 2022 (Θέματα & Λύσεις)
Τα σημερινά θέματα.
- Συνημμένα
-
- them_math_gel_220606.pdf
- (249.01 KiB) Μεταφορτώθηκε 661 φορές
Κάθε πρόβλημα έχει μία τουλάχιστον λύση!!!
Re: Μαθηματικά προσανατολισμού 2022 (Θέματα & Λύσεις)
Τα θέματα σε word
Γιατί πάντα αριθμόν έχοντι. Άνευ τούτου ουδέν νοητόν και γνωστόν.
- Πρωτοπαπάς Λευτέρης
- Συντονιστής
- Δημοσιεύσεις: 2937
- Εγγραφή: Τετ Οκτ 14, 2009 12:20 am
- Τοποθεσία: Πετρούπολη, Αθήνα
- Επικοινωνία:
Re: Μαθηματικά προσανατολισμού 2022 (Θέματα & Λύσεις)
Θέμα 1
Α1. Θεωρία στο σχολικό βιβλίο στη σελίδα 186.
Α2. Θεωρία στο σχολικό βιβλίο στη σελίδα 192.
Α3. Θεωρία στο σχολικό βιβλίο στη σελίδα 161.
Α4. α) Σ , β) Σ , γ) Σ , δ) Λ , ε) Λ.
Θέμα 2
Για![x \in D_f=(-\infty,1], x \in D_f=(-\infty,1],](/forum/ext/geomar/texintegr/latexrender/pictures/b9adda6495ed602e9d773ab2d34b2d89.png) ισχύει ότι
ισχύει ότι 
Επίσης
B1. Έχουμε ότι:
![\displaystyle{\left\{ x \in D_g : g(x) \in D_f \right\}=\left\{ x \in [0,+\infty) : \sqrt{x} \in (-\infty,1] \right\}=} \displaystyle{\left\{ x \in D_g : g(x) \in D_f \right\}=\left\{ x \in [0,+\infty) : \sqrt{x} \in (-\infty,1] \right\}=}](/forum/ext/geomar/texintegr/latexrender/pictures/df530cfa9d7c9a18bd3eeb61369f49e4.png)
![\displaystyle{=\left\{x \geq 0 : \sqrt{x} \leq 1 \right\}=\left\{x \geq 0 : x\leq 1 \right\}=[0,1] \neq \varnothing,} \displaystyle{=\left\{x \geq 0 : \sqrt{x} \leq 1 \right\}=\left\{x \geq 0 : x\leq 1 \right\}=[0,1] \neq \varnothing,}](/forum/ext/geomar/texintegr/latexrender/pictures/dd89dac59f62e25b805dcab6697c860a.png)
άρα![D_h=D_{f \circ g} = [0,1]. D_h=D_{f \circ g} = [0,1].](/forum/ext/geomar/texintegr/latexrender/pictures/521afcf13ee7b37f0123b3861c3f9ff4.png)
Συνεπώς:
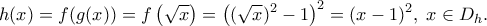
B2. H συνάρτηση είναι συνεχής και παραγωγίσιμη στο
είναι συνεχής και παραγωγίσιμη στο ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) ως πολυωυμική, με
ως πολυωυμική, με 
Για , ισχύει
, ισχύει 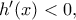 οπότε η
οπότε η  είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) ως συνεχής στο
ως συνεχής στο ![[0,1]. [0,1].](/forum/ext/geomar/texintegr/latexrender/pictures/5477054a4f15a08ccb4fce88af75dcb7.png)
Αφού η είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο ![[0,1], [0,1],](/forum/ext/geomar/texintegr/latexrender/pictures/d46be37163fdfc204e95d257d0515696.png) άρα και 1-1, οπότε η
άρα και 1-1, οπότε η  αντιστρέφεται.
αντιστρέφεται.
H είναι γνησίως φθίνουσα και συνεχής στο
είναι γνησίως φθίνουσα και συνεχής στο ![[0,1], [0,1],](/forum/ext/geomar/texintegr/latexrender/pictures/d46be37163fdfc204e95d257d0515696.png) οπότε
οπότε
![h(D_h)=[h(1),h(0)]=[0,1] h(D_h)=[h(1),h(0)]=[0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/4ab1af7a03127b8b20c3e61bf6cd412c.png) και κατά συνέπεια το πεδίο ορισμού της
και κατά συνέπεια το πεδίο ορισμού της 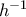 είναι το
είναι το ![D_{h^{-1}}=[0,1]. D_{h^{-1}}=[0,1].](/forum/ext/geomar/texintegr/latexrender/pictures/ecef2e6705213ced85323ab45a2a7f08.png)
Τότε για![x\in[0,1], x\in[0,1],](/forum/ext/geomar/texintegr/latexrender/pictures/5efd9ab836dec526d165fa311ce57480.png)
![y \in [0,1], y \in [0,1],](/forum/ext/geomar/texintegr/latexrender/pictures/377874e72a8dc7573bcc683f95005798.png) ισχύει:
ισχύει:
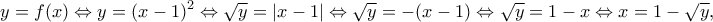
άρα![\displaystyle{h^{-1}(x)=1-\sqrt{x},\;x \in [0,1].} \displaystyle{h^{-1}(x)=1-\sqrt{x},\;x \in [0,1].}](/forum/ext/geomar/texintegr/latexrender/pictures/860c47fc9f494039e5a18b7f8ee24eb6.png)
Β3. Έχουμε ότι

(i) H συνάρτηση είναι συνεχής στο
είναι συνεχής στο  ως πηλίκο των συνεχών
ως πηλίκο των συνεχών 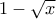 (διαφορά των συνεχών
(διαφορά των συνεχών  - σταθερή - και
- σταθερή - και  ) με την
) με την  (πολυωνυμική).
(πολυωνυμική).
Επίσης:
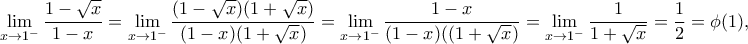
οπότε η είναι συνεχής στο
είναι συνεχής στο 
Τέλος
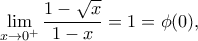
οπότε η είναι συνεχής στο
είναι συνεχής στο 
Συνεπώς η είναι συνεχής στο
είναι συνεχής στο ![[0,1]. [0,1].](/forum/ext/geomar/texintegr/latexrender/pictures/5477054a4f15a08ccb4fce88af75dcb7.png)
Επιπλέον:
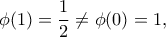
οπότε ικανοποιούνται οι προϋποθέσεις του θεωρήματος ενδιαμέσων τιμών για τη συνάρτηση στο
στο ![[0,1]. [0,1].](/forum/ext/geomar/texintegr/latexrender/pictures/5477054a4f15a08ccb4fce88af75dcb7.png)
(ii) Η συνάρτηση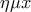 είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο 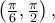 οπότε
οπότε
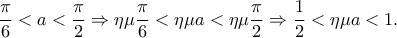
Επομένως
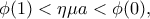
και δεδομένου ότι η ικανοποιεί τις προϋποθέσεις του θεωρήματος ενδιαμέσων τιμών, υπάρχει
ικανοποιεί τις προϋποθέσεις του θεωρήματος ενδιαμέσων τιμών, υπάρχει  έτσι ώστε
έτσι ώστε 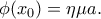
Α1. Θεωρία στο σχολικό βιβλίο στη σελίδα 186.
Α2. Θεωρία στο σχολικό βιβλίο στη σελίδα 192.
Α3. Θεωρία στο σχολικό βιβλίο στη σελίδα 161.
Α4. α) Σ , β) Σ , γ) Σ , δ) Λ , ε) Λ.
Θέμα 2
Για
![x \in D_f=(-\infty,1], x \in D_f=(-\infty,1],](/forum/ext/geomar/texintegr/latexrender/pictures/b9adda6495ed602e9d773ab2d34b2d89.png) ισχύει ότι
ισχύει ότι 
Επίσης

B1. Έχουμε ότι:
![\displaystyle{\left\{ x \in D_g : g(x) \in D_f \right\}=\left\{ x \in [0,+\infty) : \sqrt{x} \in (-\infty,1] \right\}=} \displaystyle{\left\{ x \in D_g : g(x) \in D_f \right\}=\left\{ x \in [0,+\infty) : \sqrt{x} \in (-\infty,1] \right\}=}](/forum/ext/geomar/texintegr/latexrender/pictures/df530cfa9d7c9a18bd3eeb61369f49e4.png)
![\displaystyle{=\left\{x \geq 0 : \sqrt{x} \leq 1 \right\}=\left\{x \geq 0 : x\leq 1 \right\}=[0,1] \neq \varnothing,} \displaystyle{=\left\{x \geq 0 : \sqrt{x} \leq 1 \right\}=\left\{x \geq 0 : x\leq 1 \right\}=[0,1] \neq \varnothing,}](/forum/ext/geomar/texintegr/latexrender/pictures/dd89dac59f62e25b805dcab6697c860a.png)
άρα
![D_h=D_{f \circ g} = [0,1]. D_h=D_{f \circ g} = [0,1].](/forum/ext/geomar/texintegr/latexrender/pictures/521afcf13ee7b37f0123b3861c3f9ff4.png)
Συνεπώς:
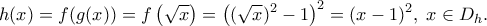
B2. H συνάρτηση
 είναι συνεχής και παραγωγίσιμη στο
είναι συνεχής και παραγωγίσιμη στο ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) ως πολυωυμική, με
ως πολυωυμική, με 
Για
 , ισχύει
, ισχύει 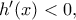 οπότε η
οπότε η  είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) ως συνεχής στο
ως συνεχής στο ![[0,1]. [0,1].](/forum/ext/geomar/texintegr/latexrender/pictures/5477054a4f15a08ccb4fce88af75dcb7.png)
Αφού η
 είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο ![[0,1], [0,1],](/forum/ext/geomar/texintegr/latexrender/pictures/d46be37163fdfc204e95d257d0515696.png) άρα και 1-1, οπότε η
άρα και 1-1, οπότε η  αντιστρέφεται.
αντιστρέφεται.H
 είναι γνησίως φθίνουσα και συνεχής στο
είναι γνησίως φθίνουσα και συνεχής στο ![[0,1], [0,1],](/forum/ext/geomar/texintegr/latexrender/pictures/d46be37163fdfc204e95d257d0515696.png) οπότε
οπότε![h(D_h)=[h(1),h(0)]=[0,1] h(D_h)=[h(1),h(0)]=[0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/4ab1af7a03127b8b20c3e61bf6cd412c.png) και κατά συνέπεια το πεδίο ορισμού της
και κατά συνέπεια το πεδίο ορισμού της 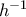 είναι το
είναι το ![D_{h^{-1}}=[0,1]. D_{h^{-1}}=[0,1].](/forum/ext/geomar/texintegr/latexrender/pictures/ecef2e6705213ced85323ab45a2a7f08.png)
Τότε για
![x\in[0,1], x\in[0,1],](/forum/ext/geomar/texintegr/latexrender/pictures/5efd9ab836dec526d165fa311ce57480.png)
![y \in [0,1], y \in [0,1],](/forum/ext/geomar/texintegr/latexrender/pictures/377874e72a8dc7573bcc683f95005798.png) ισχύει:
ισχύει: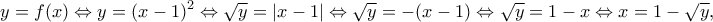
άρα
![\displaystyle{h^{-1}(x)=1-\sqrt{x},\;x \in [0,1].} \displaystyle{h^{-1}(x)=1-\sqrt{x},\;x \in [0,1].}](/forum/ext/geomar/texintegr/latexrender/pictures/860c47fc9f494039e5a18b7f8ee24eb6.png)
Β3. Έχουμε ότι

(i) H συνάρτηση
 είναι συνεχής στο
είναι συνεχής στο  ως πηλίκο των συνεχών
ως πηλίκο των συνεχών 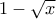 (διαφορά των συνεχών
(διαφορά των συνεχών  - σταθερή - και
- σταθερή - και  ) με την
) με την  (πολυωνυμική).
(πολυωνυμική).Επίσης:
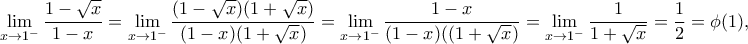
οπότε η
 είναι συνεχής στο
είναι συνεχής στο 
Τέλος
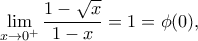
οπότε η
 είναι συνεχής στο
είναι συνεχής στο 
Συνεπώς η
 είναι συνεχής στο
είναι συνεχής στο ![[0,1]. [0,1].](/forum/ext/geomar/texintegr/latexrender/pictures/5477054a4f15a08ccb4fce88af75dcb7.png)
Επιπλέον:
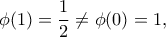
οπότε ικανοποιούνται οι προϋποθέσεις του θεωρήματος ενδιαμέσων τιμών για τη συνάρτηση
 στο
στο ![[0,1]. [0,1].](/forum/ext/geomar/texintegr/latexrender/pictures/5477054a4f15a08ccb4fce88af75dcb7.png)
(ii) Η συνάρτηση
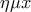 είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο 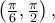 οπότε
οπότε 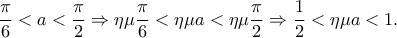
Επομένως
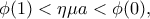
και δεδομένου ότι η
 ικανοποιεί τις προϋποθέσεις του θεωρήματος ενδιαμέσων τιμών, υπάρχει
ικανοποιεί τις προϋποθέσεις του θεωρήματος ενδιαμέσων τιμών, υπάρχει  έτσι ώστε
έτσι ώστε 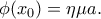
Κάθε πρόβλημα έχει μία τουλάχιστον λύση!!!
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13301
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
-
kostas.zig
- Δημοσιεύσεις: 533
- Εγγραφή: Κυρ Δεκ 21, 2008 3:29 pm
Re: Μαθηματικά προσανατολισμού 2022 (Θέματα & Λύσεις)
Ένα αρχείο geogebra για το θέμα Γ
Το σημείο μπήκε κατά λάθος πάνω στην συνάρτηση και όχι στην ευθεία που είναι το σωστό (ΜΕ συγχωρείτε...), οπότε διαγράφεται. Το σωστό σχήμα είναι παρκάτω σε δημοσίευση!
Το σημείο μπήκε κατά λάθος πάνω στην συνάρτηση και όχι στην ευθεία που είναι το σωστό (ΜΕ συγχωρείτε...), οπότε διαγράφεται. Το σωστό σχήμα είναι παρκάτω σε δημοσίευση!
τελευταία επεξεργασία από kostas.zig σε Δευ Ιουν 06, 2022 7:05 pm, έχει επεξεργασθεί 2 φορές συνολικά.
Ζυγούρης Κώστας
Re: Μαθηματικά προσανατολισμού 2022 (Θέματα & Λύσεις)
Αν για να αιτιολογήσω το τελευταίο ερώτημα έκανα άτοπο και κατέληξα με την κυρτότητα και το ελάχιστο στο ότι  αντί να δείξω απευθείας της ανίσωση υπάρχει περίπτωση κάποιος βαθμολογητής να το θεωρήσει λάθος;
αντί να δείξω απευθείας της ανίσωση υπάρχει περίπτωση κάποιος βαθμολογητής να το θεωρήσει λάθος;
 αντί να δείξω απευθείας της ανίσωση υπάρχει περίπτωση κάποιος βαθμολογητής να το θεωρήσει λάθος;
αντί να δείξω απευθείας της ανίσωση υπάρχει περίπτωση κάποιος βαθμολογητής να το θεωρήσει λάθος;Re: Μαθηματικά προσανατολισμού 2022 (Θέματα & Λύσεις)
Στο Δ3 είναι κλειδί ότι 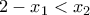 ή ισοδύναμα
ή ισοδύναμα 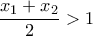 .
.
Φυσικά, ο πιο εύκολος τρόπος είναι από το Δ2.
Το πρωί στο σχολείο αναρτωτιόμουν αν υπάρχει και άλλος τρόπος. Πράγματι, ένας άλλος τρόπος είναι ο εξής:
Μια "γνωστή" ανισότητα είναι η ανισότητα λογαριθμικού-αριθμητικού μέσου: Αν , τότε
, τότε
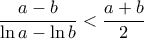 (*)
(*)
Από αυτή με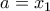 και
και  παίρνουμε
παίρνουμε  ,
,
οπότε
 ,
,
και άρα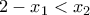 κτλ.
κτλ.
* Ισοδύναμα για τη συνάρτηση είναι
είναι 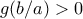 .
.
[Απόδειξη: Πράγματι, η έχει
έχει  και
και 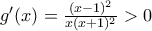 για
για 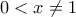 . Αφού
. Αφού 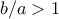 , έπεται ότι
, έπεται ότι 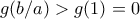 .]
.]
Φιλικά,
Αχιλλέας
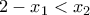 ή ισοδύναμα
ή ισοδύναμα 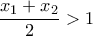 .
.Φυσικά, ο πιο εύκολος τρόπος είναι από το Δ2.
Το πρωί στο σχολείο αναρτωτιόμουν αν υπάρχει και άλλος τρόπος. Πράγματι, ένας άλλος τρόπος είναι ο εξής:
Μια "γνωστή" ανισότητα είναι η ανισότητα λογαριθμικού-αριθμητικού μέσου: Αν
 , τότε
, τότε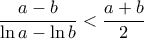 (*)
(*)Από αυτή με
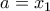 και
και  παίρνουμε
παίρνουμε  ,
,οπότε
 ,
,και άρα
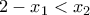 κτλ.
κτλ.* Ισοδύναμα για τη συνάρτηση
 είναι
είναι 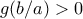 .
. [Απόδειξη: Πράγματι, η
 έχει
έχει  και
και 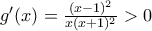 για
για 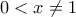 . Αφού
. Αφού 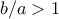 , έπεται ότι
, έπεται ότι 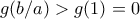 .]
.]Φιλικά,
Αχιλλέας
- Συνημμένα
-
- Screenshot 2022-06-06 at 6.45.16 PM.png (103.22 KiB) Προβλήθηκε 3686 φορές
- emouroukos
- Συντονιστής
- Δημοσιεύσεις: 1447
- Εγγραφή: Δευ Δεκ 22, 2008 1:27 pm
- Τοποθεσία: Αγρίνιο
Re: Μαθηματικά προσανατολισμού 2022 (Θέματα & Λύσεις)
Μια άλλη προσέγγιση για το Δ4, χωρίς κυρτότητα ή ΘΜΤ, αλλά με (κάποιες) πράξεις:
Θεωρούμε τη συνάρτηση
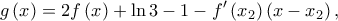
με .
.
Η είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  , με
, με
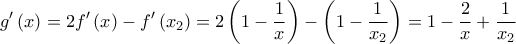
για κάθε .
.
Είναι:
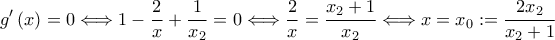
και

Eπομένως, η παρουσιάζει ολικό ελάχιστο στο
παρουσιάζει ολικό ελάχιστο στο  . Θα αποδείξουμε ότι
. Θα αποδείξουμε ότι 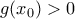 , οπότε θα είναι
, οπότε θα είναι  για κάθε
για κάθε  και η δοσμένη εξίσωση είναι αδύνατη. Πράγματι, είναι:
και η δοσμένη εξίσωση είναι αδύνατη. Πράγματι, είναι:
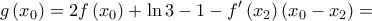

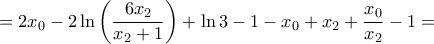

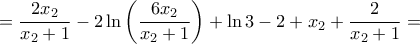
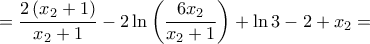
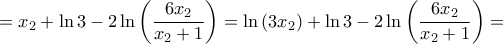
![\displaystyle{
=\ln \left[ \frac{9x_2}{\frac{36x_{2}^{2}}{\left( x_2+1 \right) ^2}} \right] =\ln \left[ \frac{\left( x_2+1 \right) ^2}{4x_2} \right] >\ln 1=0,
} \displaystyle{
=\ln \left[ \frac{9x_2}{\frac{36x_{2}^{2}}{\left( x_2+1 \right) ^2}} \right] =\ln \left[ \frac{\left( x_2+1 \right) ^2}{4x_2} \right] >\ln 1=0,
}](/forum/ext/geomar/texintegr/latexrender/pictures/10c6482b283d8fedfd1a4ef0d9c2db8f.png)
αφού
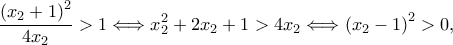
που ισχύει.
Θεωρούμε τη συνάρτηση
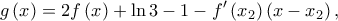
με
 .
.Η
 είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  , με
, με 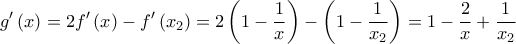
για κάθε
 .
.Είναι:
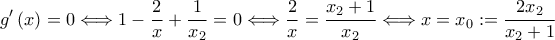
και

Eπομένως, η
 παρουσιάζει ολικό ελάχιστο στο
παρουσιάζει ολικό ελάχιστο στο  . Θα αποδείξουμε ότι
. Θα αποδείξουμε ότι 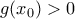 , οπότε θα είναι
, οπότε θα είναι  για κάθε
για κάθε  και η δοσμένη εξίσωση είναι αδύνατη. Πράγματι, είναι:
και η δοσμένη εξίσωση είναι αδύνατη. Πράγματι, είναι: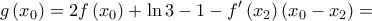

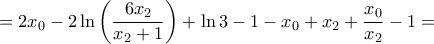

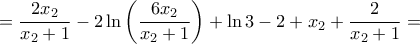
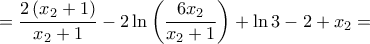
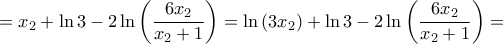
![\displaystyle{
=\ln \left[ \frac{9x_2}{\frac{36x_{2}^{2}}{\left( x_2+1 \right) ^2}} \right] =\ln \left[ \frac{\left( x_2+1 \right) ^2}{4x_2} \right] >\ln 1=0,
} \displaystyle{
=\ln \left[ \frac{9x_2}{\frac{36x_{2}^{2}}{\left( x_2+1 \right) ^2}} \right] =\ln \left[ \frac{\left( x_2+1 \right) ^2}{4x_2} \right] >\ln 1=0,
}](/forum/ext/geomar/texintegr/latexrender/pictures/10c6482b283d8fedfd1a4ef0d9c2db8f.png)
αφού
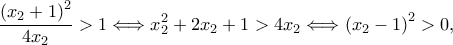
που ισχύει.
Βαγγέλης Μουρούκος
Erro ergo sum.
Erro ergo sum.
-
Pantelis.N
- Δημοσιεύσεις: 26
- Εγγραφή: Σάβ Απρ 20, 2019 10:00 pm
Re: Μαθηματικά προσανατολισμού 2022 (Θέματα & Λύσεις)
Στο θέμα Γ4 πήρα λάθος κλάδο για τον υπολογισμό του δεύτερου ορίου.
Στο Δ4 έκανα ένα μεγάλο λάθος...από λάθη σε πράξεις έβγαλα ότι με βάση το θεώρημα Μπολζάνο υπάρχει λύση και μετά δεν ξανακοίταξα τη λύση μου. Έχοντας βρει την εξίσωση της εφαπτομένης στο και αναφέροντας τα περί κυρτότητας και θεωρώντας πως τα λάθη μου είναι μόνο αυτά που ανέφερα, πόσο μπορώ να περιμένω πως θα πάρω;
Πραγματικά έχω απογοητευθεί πλήρως από την τραγική μου επίδοση.
Στο Δ4 έκανα ένα μεγάλο λάθος...από λάθη σε πράξεις έβγαλα ότι με βάση το θεώρημα Μπολζάνο υπάρχει λύση και μετά δεν ξανακοίταξα τη λύση μου. Έχοντας βρει την εξίσωση της εφαπτομένης στο και αναφέροντας τα περί κυρτότητας και θεωρώντας πως τα λάθη μου είναι μόνο αυτά που ανέφερα, πόσο μπορώ να περιμένω πως θα πάρω;
Πραγματικά έχω απογοητευθεί πλήρως από την τραγική μου επίδοση.
- Tolaso J Kos
- Δημοσιεύσεις: 5237
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: Μαθηματικά προσανατολισμού 2022 (Θέματα & Λύσεις)
Για μένα κοιτάς παρακάτω. Ό, τι έγινε , έγινε! Δεν σε ανησυχεί ... το κεφάλι ψηλά και κοιτάς το επόμενο μάθημα. Ό, τι και να σου πούμε εμείς τώρα πιο πολύ άγχος θα σου μεταδώσουμε!!
Καλή συνέχεια με τα υπόλοιπα μαθήματα ... και καλά αποτελέσματα.
Η φαντασία είναι σημαντικότερη από τη γνώση !


Re: Μαθηματικά προσανατολισμού 2022 (Θέματα & Λύσεις)
Ένα σχήμα και για την συνάρτηση του - έξοχου αλλά πολύ απαιτητικού - θέματος Δ .
-
Τσιαλας Νικολαος
- Δημοσιεύσεις: 789
- Εγγραφή: Σάβ Ιαν 17, 2015 1:04 pm
Re: Μαθηματικά προσανατολισμού 2022 (Θέματα & Λύσεις)
Αγαπητέ Παντελή δεν υπάρχει λόγος απογοήτευσης! Λάθη γίνονται και θα γίνονται μια ζωή! Συνέχισε δυνατά και στα αλλά 2 μαθήματα και τίποτα δεν εχει χαθεί!Pantelis.N έγραψε: ↑Δευ Ιουν 06, 2022 7:40 pmΣτο θέμα Γ4 πήρα λάθος κλάδο για τον υπολογισμό του δεύτερου ορίου.
Στο Δ4 έκανα ένα μεγάλο λάθος...από λάθη σε πράξεις έβγαλα ότι με βάση το θεώρημα Μπολζάνο υπάρχει λύση και μετά δεν ξανακοίταξα τη λύση μου. Έχοντας βρει την εξίσωση της εφαπτομένης στο και αναφέροντας τα περί κυρτότητας και θεωρώντας πως τα λάθη μου είναι μόνο αυτά που ανέφερα, πόσο μπορώ να περιμένω πως θα πάρω;
Πραγματικά έχω απογοητευθεί πλήρως από την τραγική μου επίδοση.
-
Επιτροπή Θεμάτων 2023
- Δημοσιεύσεις: 28
- Εγγραφή: Πέμ Μάιος 12, 2016 9:41 am
Re: Μαθηματικά προσανατολισμού 2022 (Θέματα & Λύσεις)
Αναρτούμε σήμερα, 6 Ιουνίου 2022, τη 1η έκδοση των λύσεων των θεμάτων Μαθηματικών προσανατολισμού 2022 η οποία είναι αποτέλεσμα συλλογικής δουλειάς των Επιμελητών του mathematica.gr.
Θέματα & Λύσεις Μαθηματικών προσαν. 2022 (1η έκδοση)
Θέματα & Λύσεις Μαθηματικών προσαν. 2022 (1η έκδοση)

-
Pantelis.N
- Δημοσιεύσεις: 26
- Εγγραφή: Σάβ Απρ 20, 2019 10:00 pm
Re: Μαθηματικά προσανατολισμού 2022 (Θέματα & Λύσεις)
Σας ευχαριστώ για τα καλά σας λόγια.
Οι εκτιμήσεις των καθηγητών μου είναι από 92 στην χειρότερη περίπτωση μέχρι και 96 στην καλύτερη.
Ίσως με σώζει το γεγονός ότι θα ανέβουν οι βάσεις και από όσο έμαθα οι μαθητές δυσκολεύθηκαν πιο πολύ στο Δ3, πολύ λίγοι υποψήφιοι το έχουν λύσει, ενώ πάρα πολλά άτομα την πάτησαν στο Γ4 στην επιλογή κλάδου.
Οι εκτιμήσεις των καθηγητών μου είναι από 92 στην χειρότερη περίπτωση μέχρι και 96 στην καλύτερη.
Ίσως με σώζει το γεγονός ότι θα ανέβουν οι βάσεις και από όσο έμαθα οι μαθητές δυσκολεύθηκαν πιο πολύ στο Δ3, πολύ λίγοι υποψήφιοι το έχουν λύσει, ενώ πάρα πολλά άτομα την πάτησαν στο Γ4 στην επιλογή κλάδου.
Re: Μαθηματικά προσανατολισμού 2022 (Θέματα & Λύσεις)
Καλησπέρα,
Παρατήρησα ότι για το Δ.4 θέμα κυκλοφορούν στο διαδίκτυο και στο site του mathematica δύο τρόποι επίλυσης, κυρίως με την εφαπτομένη και με το να θεωρήσουμε συνάρτηση η οποία έχει θετικό ολικό ακρότατο. Το έλυσα με εναν διαφορετικό τρόπο, εφαρμόζοντας Θεωρημα Μέσης Τιμής δύο φορές. Θα ήθελα να μου πείτε αν είναι σωστή ή αν υπάρχει κάτι μεμπτό στη λύση. Επισυνάπτω στις φωτογραφίες τη λύση μου.
Παρατήρησα ότι για το Δ.4 θέμα κυκλοφορούν στο διαδίκτυο και στο site του mathematica δύο τρόποι επίλυσης, κυρίως με την εφαπτομένη και με το να θεωρήσουμε συνάρτηση η οποία έχει θετικό ολικό ακρότατο. Το έλυσα με εναν διαφορετικό τρόπο, εφαρμόζοντας Θεωρημα Μέσης Τιμής δύο φορές. Θα ήθελα να μου πείτε αν είναι σωστή ή αν υπάρχει κάτι μεμπτό στη λύση. Επισυνάπτω στις φωτογραφίες τη λύση μου.
-
Λευτέρης Παπανικολάου
- Δημοσιεύσεις: 109
- Εγγραφή: Κυρ Νοέμ 02, 2014 11:25 pm
- Τοποθεσία: Πάτρα
Re: Μαθηματικά προσανατολισμού 2022 (Θέματα & Λύσεις)
Ό,τι έγινε, έγινε. Να κοιτάς μπροστά και θα πας μπροστά. Καλή συνέχεια στα επόμεναPantelis.N έγραψε: ↑Δευ Ιουν 06, 2022 7:40 pmΣτο θέμα Γ4 πήρα λάθος κλάδο για τον υπολογισμό του δεύτερου ορίου.
Στο Δ4 έκανα ένα μεγάλο λάθος...από λάθη σε πράξεις έβγαλα ότι με βάση το θεώρημα Μπολζάνο υπάρχει λύση και μετά δεν ξανακοίταξα τη λύση μου. Έχοντας βρει την εξίσωση της εφαπτομένης στο και αναφέροντας τα περί κυρτότητας και θεωρώντας πως τα λάθη μου είναι μόνο αυτά που ανέφερα, πόσο μπορώ να περιμένω πως θα πάρω;
Πραγματικά έχω απογοητευθεί πλήρως από την τραγική μου επίδοση.
Re: Μαθηματικά προσανατολισμού 2022 (Θέματα & Λύσεις)
Σωστή είναι η λύση σου.JimKas έγραψε: ↑Τρί Ιουν 07, 2022 12:34 amΚαλησπέρα,
Παρατήρησα ότι για το Δ.4 θέμα κυκλοφορούν στο διαδίκτυο και στο site του mathematica δύο τρόποι επίλυσης, κυρίως με την εφαπτομένη και με το να θεωρήσουμε συνάρτηση η οποία έχει θετικό ολικό ακρότατο. Το έλυσα με εναν διαφορετικό τρόπο, εφαρμόζοντας Θεωρημα Μέσης Τιμής δύο φορές. Θα ήθελα να μου πείτε αν είναι σωστή ή αν υπάρχει κάτι μεμπτό στη λύση. Επισυνάπτω στις φωτογραφίες τη λύση μου.
Ουσιαστικά χρησιμοποιείς αποδεικτικά την πρόταση ότι η εφαπτομένη στο
 είναι πιο κάτω από την γραφική παράσταση της συνάρτησης.
είναι πιο κάτω από την γραφική παράσταση της συνάρτησης.

Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες

 χωρίς παράγωγο.
χωρίς παράγωγο.