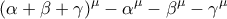 όπου
όπου  περιττός θετικός, διαιρείται από το γινόμενο
περιττός θετικός, διαιρείται από το γινόμενο 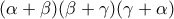
2. Να δειχθεί οτι η παράσταση
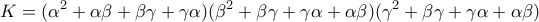 είναι τετράγωνο μιας άλλης ρητής παράστασης ως προς
είναι τετράγωνο μιας άλλης ρητής παράστασης ως προς  και να βρεθεί αυτή.
και να βρεθεί αυτή.3. Να λυθεί το σύστημα
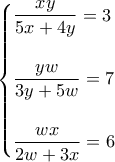
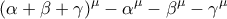 όπου
όπου  περιττός θετικός, διαιρείται από το γινόμενο
περιττός θετικός, διαιρείται από το γινόμενο 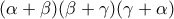
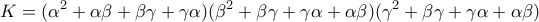 είναι τετράγωνο μιας άλλης ρητής παράστασης ως προς
είναι τετράγωνο μιας άλλης ρητής παράστασης ως προς  και να βρεθεί αυτή.
και να βρεθεί αυτή.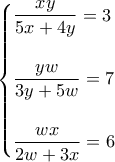
Το θέμα αυτό σκοπεύω να το θέσω στα τρία τμήματα Γ' Γυμνασίου που έχω φέτος, για αυτό το λύνω...parmenides51 έγραψε: ↑Τρί Νοέμ 05, 2013 8:20 am
2. Να δειχθεί οτι η παράστασηείναι τετράγωνο μιας άλλης ρητής παράστασης ως προς
και να βρεθεί αυτή.
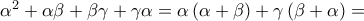
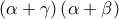
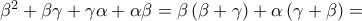
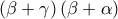
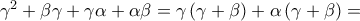
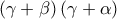
![K=\left ( \alpha +\beta \right )^{2}\left ( \beta +\gamma \right )^{2}\left ( \gamma +\alpha \right )^{2}=\left [ \left ( \alpha +\beta \right )\left ( \beta +\gamma \right )\left ( \gamma +\alpha \right ) \right ]^{2} K=\left ( \alpha +\beta \right )^{2}\left ( \beta +\gamma \right )^{2}\left ( \gamma +\alpha \right )^{2}=\left [ \left ( \alpha +\beta \right )\left ( \beta +\gamma \right )\left ( \gamma +\alpha \right ) \right ]^{2}](/forum/ext/geomar/texintegr/latexrender/pictures/f2c613198210547dd0217034d8f9fe4b.png)
Έστωparmenides51 έγραψε: ↑Τρί Νοέμ 05, 2013 8:20 am1. Να δείξετε οτι το πολυώνυμοόπου
περιττός θετικός, διαιρείται από το γινόμενο
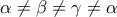
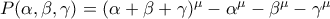 τότε
τότε 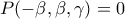 άρα
άρα 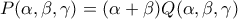 .
.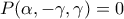 ενώ
ενώ 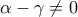 άρα
άρα 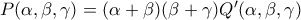
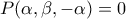 και
και 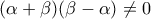 άρα
άρα 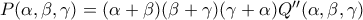
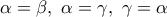 , ας είναι
, ας είναι 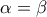 και
και 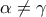
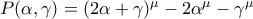 , παρατηρούμε ότι:
, παρατηρούμε ότι: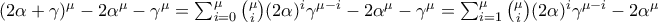
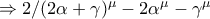
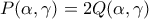
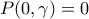 συνεπώς
συνεπώς 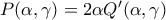 και
και 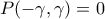 άρα
άρα 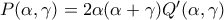 ...εδώ έχω κολλήσει....
...εδώ έχω κολλήσει....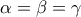
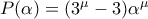 η απαίτηση
η απαίτηση 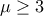 είναι επιτακτική. Μπορούμε να δούμε ότι
είναι επιτακτική. Μπορούμε να δούμε ότι 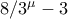 καθώς επαληθεύεται με επαγωγή. Δηλαδή
καθώς επαληθεύεται με επαγωγή. Δηλαδή 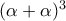 διαιρεί το
διαιρεί το 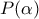
 είναι διαφορετικά μεταξύ τους. Θέλω να πω ότι το πρώτο μέρος της λύσης σου, επαρκούσε για τους τότε υποψηφίους.
είναι διαφορετικά μεταξύ τους. Θέλω να πω ότι το πρώτο μέρος της λύσης σου, επαρκούσε για τους τότε υποψηφίους. Τώρα, αν θέλουμε να συνεχίσουμε, όπως πολύ ορθά κάνεις, έχουμε δύο τρόπους. Σπεύδω να τονίσω ότι είναι εκτός ύλης για το Μικρό Πολυτεχνείο, αν και επιτρεπτό σήμερα.Christos.N έγραψε: ↑Δευ Μαρ 15, 2021 6:50 pmΜια μερική απάντηση
Άρα
επίσηςσυνεπώς
και
άρα
...εδώ έχω κολλήσει....
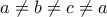 , παίρνουμε όριο
, παίρνουμε όριο 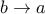 , οπότε έπεται και η περίπτωση
, οπότε έπεται και η περίπτωση  .
. . Έδειξες λοιπόν ότι το
. Έδειξες λοιπόν ότι το 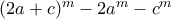 για
για  περιττό, έχει ρίζα την
περιττό, έχει ρίζα την 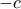 . Θέλουμε να δείξουμε ακόμα ότι είναι διπλή ρίζα. Απλά παραγωγίζουμε ως προς
. Θέλουμε να δείξουμε ακόμα ότι είναι διπλή ρίζα. Απλά παραγωγίζουμε ως προς  και βάζουμε
και βάζουμε 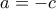 (άμεσο ότι μηδενίζεται).
(άμεσο ότι μηδενίζεται). 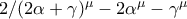 . Αυτό περιττεύει γιατί εδώ εννοείται η διαιρετότητα πολυωνύμων, όχι αριθμών. Για παράδειγμα στα πολυώνυμα το
. Αυτό περιττεύει γιατί εδώ εννοείται η διαιρετότητα πολυωνύμων, όχι αριθμών. Για παράδειγμα στα πολυώνυμα το 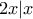 επιτρέπεται (έπεται από τον ορισμό), πράγμα που βέβαια δεν ισχύει στους αριθμούς.
επιτρέπεται (έπεται από τον ορισμό), πράγμα που βέβαια δεν ισχύει στους αριθμούς.Κύριε Μιχάλη ευχαριστώ πάρα πολύ, δεν το σκέφτηκα αυτό με την παράγωγο γιατί επέμενα σε συγκεκριμένο πλαίσιο. Τώρα αυτό με την διαιρετότητα με δεύτερη ματιά καταλαβαίνω πόσο ανούσιο είναι, αλίμονο στον λύτη που έχει αγκυλώσεις.Mihalis_Lambrou έγραψε: ↑Δευ Μαρ 15, 2021 7:47 pm
β) Κοιτάμε (όπως έκανες) το αριστερό μέλος ως πολυώνυμο του. Έδειξες λοιπόν ότι το
για
περιττό, έχει ρίζα την
. Θέλουμε να δείξουμε ακόμα ότι είναι διπλή ρίζα. Απλά παραγωγίζουμε ως προς
και βάζουμε
(άμεσο ότι μηδενίζεται).
Και ένα τελευταίο: Έδειξες ότι. Αυτό περιττεύει γιατί εδώ εννοείται η διαιρετότητα πολυωνύμων, όχι αριθμών. Για παράδειγμα στα πολυώνυμα το
επιτρέπεται (έπεται από τον ορισμό), πράγμα που βέβαια δεν ισχύει στους αριθμούς.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης