parmenides51 έγραψε:
2. Σε τρίγωνο

δίνονται
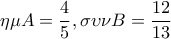
και
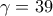
μέτρα.
Να βρεθεί η πλευρά
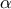
και το εμβαδόν

.
Δεν πρόκειται να σας κουράσω με την αναγραφή πολλών πράξεων....
Από τα πολύ βασικά της σχολικής τριγωνομετρίας προκύπτει εύκολα ότι
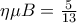
και ότι
ή
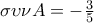
, κάτι που σημαίνει ότι η

είναι αμβλεία
ή
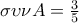
, κάτι που σημαίνει ότι η

είναι οξεία.
Θα εξετάσουμε και τις δύο περιπτώσεις.
Ας ξεκινήσουμε με την περίπτωση
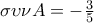
Αν θυμηθούμε το θεώρημα των προβολών , έχουμε ότι
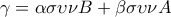
δηλαδή
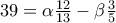

Aς θυμηθούμε τώρα και το νόμο των ημιτόνων , θα έχουμε
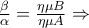
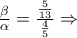
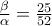

Έγραψα πριν ότι δε σκοπεύω να σας κουράσω με πράξεις , λύνουμε λοιπόν το σύστημα των

και

, για ένα γραμμικό σύστημα πρόκειται , καταλήγουμε ότι
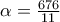
( και
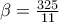
)
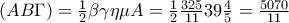
ή αν δε θέλουμε να χρησιμοποιήσουμε το

, μπορούμε να γράψουμε
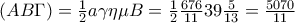
Ας δούμε και την περίπτωση
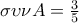
...
Η σκέψη μένει ίδια , η εξίσωση
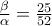

εξακολουθεί να ισχύει και το μόνο που αλλάζει είναι η εξίσωση που προκύπτει από το θεώρημα των προβολών , γίνεται
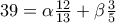
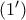
Aν λύσουμε το σύστημα των
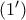
και

βρίσκουμε ότι
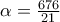
( και
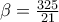
)
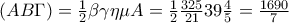
ή αν δε θέλουμε να χρησιμοποιήσουμε το

, μπορούμε να γράψουμε
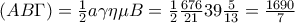 Ένας σημερινός μαθητής τι κέρδος θα έχει αν μελετήσει αυτό το θέμα;
Ένας σημερινός μαθητής τι κέρδος θα έχει αν μελετήσει αυτό το θέμα;
Να δει το θεώρημα των προβολών , στο σχολείο είναι απίθανο να το δει ....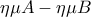 και
και 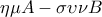
 δίνονται
δίνονται 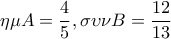 και
και 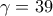 μέτρα.
μέτρα. 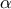 και το εμβαδόν
και το εμβαδόν  .
. μετριούνται σε ακτίνια.
μετριούνται σε ακτίνια.  τέτοιοι ώστε
τέτοιοι ώστε 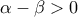 .
. 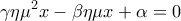 δεν έχει καμία λύση ως προς
δεν έχει καμία λύση ως προς  .
.
 ισχύει:
ισχύει: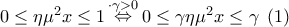
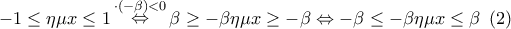
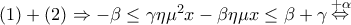
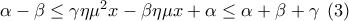
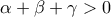 και
και 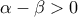 από τη σχέση
από τη σχέση  προκύπτει ότι:
προκύπτει ότι: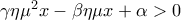 για κάθε
για κάθε 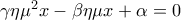 είναι αδύνατη.
είναι αδύνατη.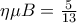
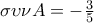 , κάτι που σημαίνει ότι η
, κάτι που σημαίνει ότι η  είναι αμβλεία
είναι αμβλεία 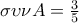 , κάτι που σημαίνει ότι η
, κάτι που σημαίνει ότι η 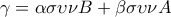
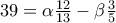

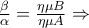
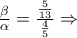
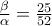

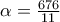 ( και
( και 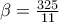 )
)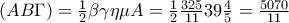
 , μπορούμε να γράψουμε
, μπορούμε να γράψουμε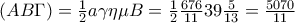
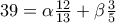
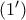
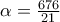 ( και
( και 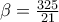 )
)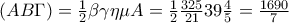
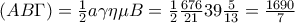
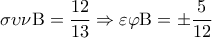
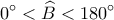 και αφού
και αφού 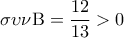 είναι
είναι 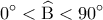 , οπότε και
, οπότε και 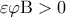 , άρα
, άρα 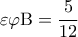
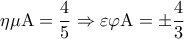
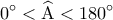 , οπότε
, οπότε 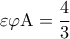 .
.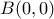 παίρνουμε
παίρνουμε 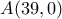 και κατασκευάζουμε τις ευθείες
και κατασκευάζουμε τις ευθείες 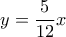 και
και 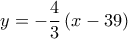 που ορίζουν τις
που ορίζουν τις  αντίστοιχα και τέμνονται στο
αντίστοιχα και τέμνονται στο 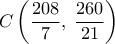
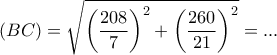 και
και 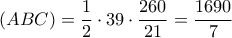
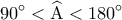 , οπότε
, οπότε 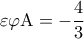 .
.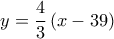 που ορίζουν τις
που ορίζουν τις 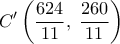
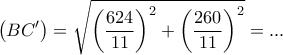 και
και 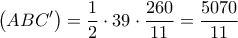
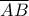 . Για παράδειγμα αν
. Για παράδειγμα αν  είναι το ύψος ορθογωνίου τριγώνου
είναι το ύψος ορθογωνίου τριγώνου 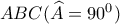 , γράφαμε:
, γράφαμε: 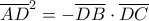 .
.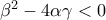 τότε η εξίσωση δεν έχει λύσεις.
τότε η εξίσωση δεν έχει λύσεις.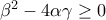 . Tότε υπάρχουν δύο πραγματικές λύσεις .
. Tότε υπάρχουν δύο πραγματικές λύσεις .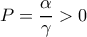 , άρα οι λύσεις είναι ομόσημες.
, άρα οι λύσεις είναι ομόσημες.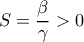 , άρα οι λύσεις είναι θετικές.
, άρα οι λύσεις είναι θετικές. και ας μην ξεχνάμε ότι παριστάνουν τιμές ημιτόνου , άρα ισχύει ότι
και ας μην ξεχνάμε ότι παριστάνουν τιμές ημιτόνου , άρα ισχύει ότι 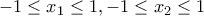
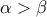 μπορούμε να γράψουμε ότι
μπορούμε να γράψουμε ότι 
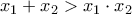
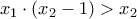
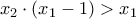
 .
.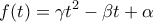
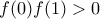 .
.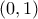 η και οι δύο είναι εκτός η δεν είναι πραγματικές.
η και οι δύο είναι εκτός η δεν είναι πραγματικές.![[-1,1] [-1,1]](/forum/ext/geomar/texintegr/latexrender/pictures/d060b17b29e0dae91a1cac23ea62281a.png)