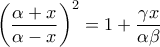
2. Μετά από πόσα έτη ένα κεφάλαιο
 δραχμών αναλογιζόμενο προς
δραχμών αναλογιζόμενο προς  γίνεται
γίνεται  δρχ ;
δρχ ; (εαν ο αριθμός των ετών δεν είναι ακέραιος να βρεθεί και το κλάσμα)
3. Να μετατραπεί διπλό ριζικό σε αλγεβρικό άθροισμα απλών ριζικών.
4. Πότε η διαίρεση
 είναι τέλεια;
είναι τέλεια; Να βρεθεί το πηλίκο χωρίς να εκτελεσθεί η διαίρεση.

 και
και  .
. Αν
Αν  έχουμε την εξίσωση
έχουμε την εξίσωση 
 έχουμε ισοδύναμα
έχουμε ισοδύναμα

 . Αφού
. Αφού  η εξίσωση είναι δευτέρου βαθμού με διακρίνουσα
η εξίσωση είναι δευτέρου βαθμού με διακρίνουσα
 Αν
Αν  τότε
τότε  και η εξίσωση έχει ρίζες
και η εξίσωση έχει ρίζες 
 τότε
τότε  και η εξίσωση έχει ρίζες
και η εξίσωση έχει ρίζες 
 . Για να είναι η διαίρεση τέλεια, πρέπει και αρκεί
. Για να είναι η διαίρεση τέλεια, πρέπει και αρκεί .
.
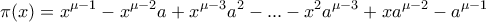
 σε αλγεβρικό άθροισμα δύο απλών ριζικών.
σε αλγεβρικό άθροισμα δύο απλών ριζικών. ρητοί αριθμοί με
ρητοί αριθμοί με 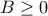 )
) και
και  , έτσι ώστε να είναι:
, έτσι ώστε να είναι:
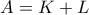 και
και  , δηλαδή
, δηλαδή  και
και 
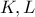 είναι οι ρίζες της εξίσωσης
είναι οι ρίζες της εξίσωσης 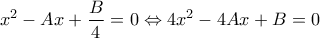
 . Για να υπάρχουν ρίζες ρητές, πρέπει ο αριθμός
. Για να υπάρχουν ρίζες ρητές, πρέπει ο αριθμός  να είναι τέλειο τετράγωνο ρητού. Δηλαδή
να είναι τέλειο τετράγωνο ρητού. Δηλαδή 
 , από όπου και προκύπτει ότι:
, από όπου και προκύπτει ότι: , με
, με 

 ,με
,με  ρητοί,
ρητοί, άρρητοι,τότε
άρρητοι,τότε 


 , ρητός ---> άτοπο
, ρητός ---> άτοπο
 να ήταν ρητός, γιατί τότε δεν θα
να ήταν ρητός, γιατί τότε δεν θα  θα μπορούσε να ήταν ρητός, γιατί τότε θα έπρεπε να ήταν
θα μπορούσε να ήταν ρητός, γιατί τότε θα έπρεπε να ήταν είναι το τελικό κεφάλαιο ,
είναι το τελικό κεφάλαιο ,  το αρχικό κεφάλαιο και
το αρχικό κεφάλαιο και  το επιτόκιο , τότε ισχύει ότι
το επιτόκιο , τότε ισχύει ότι  , όπου
, όπου  ο αριθμός των ετών που μεσολαβούν έτσι ώστε το αρχικό κεφάλαιο να φτάσει στο ύψος του τελικού κεφαλαίου.
ο αριθμός των ετών που μεσολαβούν έτσι ώστε το αρχικό κεφάλαιο να φτάσει στο ύψος του τελικού κεφαλαίου. και έτσι
και έτσι 
 , δηλαδή
, δηλαδή  . Το τελικό αποτέλεσμα είναι
. Το τελικό αποτέλεσμα είναι  έτη.
έτη. .
. η εξίσωση γίνεται:
η εξίσωση γίνεται: που ισοδυναμεί με την
που ισοδυναμεί με την 
