1. α) Οι πλευρές ενός τριγώνου υπακούουν στις σχέσεις
 .
. Να αποδειχθεί οτι το εμβαδόν του δίνεται από τον τύπο
 .
.β) Να λυθεί η εξίσωση

2. α) Να βρεθεί το άθροισμα

β) Εαν
 και
και  θετικά ποσά, λογιστά δια των λογαρίθμων και
θετικά ποσά, λογιστά δια των λογαρίθμων και  .
. Ζητείται για κατάλληλες βοηθητικές γωνίες να γίνουν λογιστές δια των λογαρίθμων
οι παραστάσεις

3. α) Σημείο O στον χώρο απέχει και από τις τρεις κορυφές τριγώνου
 του οποίου
του οποίου οι αποστάσεις είναι αντιστοίχως
 και
και  .
. Ζητείται η απόσταση του
 από το επίπεδο του τριγώνου και η δίεδρος γωνία
από το επίπεδο του τριγώνου και η δίεδρος γωνία  .
.β) Εαν οι γωνίες
 και τα αντίστοιχα ημίτονα τους, αποτελούν αντίστοιχα διαδοχικούς όρους αριθμητικής προόδου,
και τα αντίστοιχα ημίτονα τους, αποτελούν αντίστοιχα διαδοχικούς όρους αριθμητικής προόδου, να εκφραστούν δυο από τις γωνίες αυτές συναρτήσει της τρίτης.
4. Να επιλυθεί τρίγωνο
 (πλευρές και γωνίες) , του οποίου δίνονται
(πλευρές και γωνίες) , του οποίου δίνονται η διχοτόμος της γωνίας
 η διαφορά των γωνιών
η διαφορά των γωνιών 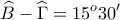
και η ακτίνα
 του εγγεγραμμένου του κύκλου.
του εγγεγραμμένου του κύκλου.Σημείωση για το 2α θέμα

Σημείωση για το 2β θέμα σχετικά με την έκφραση λογιστή δια των λογαρίθμων εδώ κι εδώ
Υ.Γ. Σύμφωνα με το Ετήσιο Δελτίο του Πάλλα :
το ερώτημα 1α ήταν λανθασμένο γιατί είχε δοθεί χωρίς απόλυτο στο ζητούμενο
το ερώτημα 1β ήταν λανθασμένο γιατί δεν μπορεί να λυθεί η συγκεκριμένη τριγωνομετρική εξίσωση
(μόνο με Θ.Bolzano σε διάφορα διαστήματα βρίσκουμε προσεγγιστικά οτι υπάρχει λύση)
το ερώτημα 2α ήταν λανθασμένο γιατί ζητείται το άθροισμα των άπειρων όρων ενώ η συγκεκριμένη σειρά είναι αποκλίνουσα
Ήταν τα 3 από τα 6 θέματα των εισαγωγικών εξετάσεων του ΕΜΠ το 1962 για τα οποία κατέθεσε μήνυση ο Αριστείδης Πάλλας
στο Συμβούλιο της Επικρατείας και ζητούσε την ακύρωση των τότε εξετάσεων. Το μέρος του πήρε η ΕΜΕ τότε.
Περισσότερα προσεχώς, θα ετοιμάσω κείμενο με δηλώσεις των συμμετεχόντων και ένα σύντομο ιστορικό.
Τα υπόλοιπα 3 θέματα ήταν τα εξής: 4ο θέμα Άλγεβρας Πολιτικών Μηχανικών
4ο θέμα Γεωμετρίας Αρχιτεκτόνων, 2β ερώτημα ΆΛγεβρας Τοπογράφων - Αγρονόμων Μηχανικών
Προτροπή: Αναζητήστε την ''Μαύρη Βίβλο των Εισαγωγικών Εξετάσεων του Εθνικού Μετσόβιου Πολυτεχνείου κατά Σεπτέμβριον 1962''
του Αριστείδου Φ. Πάλλα (περιέχει το ιστορικό των ακυρωθέντων θεμάτων και δημοσιεύματα εφημερίδων της εποχής)
Για να το διαβάσετε έχει 4 αντίτυπα η μη δανειστική Μπενάκειος Βιβλιοθήκη
η οποία στεγάζεται προς το παρόν στο Πρώην Δημόσιο Καπνεργοστάσιο (Λένορμαν 218, Αθήνα)
Τους κωδικούς τους βλέπετε με την αναζήτηση ''Η μαύρη βίβλος των εισαγωγικών εξετάσεων'' εδώ
Ώρες λειτουργίας: Δευτέρα και Τετάρτη 9:00-18:00, Τρίτη, Πέμπτη και Παρασκευή 9:00-15:00, Σάββατο 9:00-14:00
Επικοινωνία: (Αναγνωστήριο) 210 510 2059
Πληροφορίες εδώ


![\displaystyle \frac{1}{16}\left[\left(\beta +\gamma \right)^{2}-a^{2} \right]\left[ a^{2}-\left(\beta -\gamma \right)^{2}\right]=\frac{1}{16}\left(\beta ^{2}+2\beta \gamma +\gamma ^{2} -a^{2}\right)\left(a^{2}-\beta ^{2}+2\beta \gamma -\gamma ^{2} \right)= \displaystyle \frac{1}{16}\left[\left(\beta +\gamma \right)^{2}-a^{2} \right]\left[ a^{2}-\left(\beta -\gamma \right)^{2}\right]=\frac{1}{16}\left(\beta ^{2}+2\beta \gamma +\gamma ^{2} -a^{2}\right)\left(a^{2}-\beta ^{2}+2\beta \gamma -\gamma ^{2} \right)=](/forum/ext/geomar/texintegr/latexrender/pictures/055e2b1df8bbbf87d9d4fdef405cfe34.png)
![\displaystyle\frac{1}{16}\left[2\beta \gamma +\left(\beta ^{2}+\gamma ^{2}-a^{2} \right) \right]\left[2\beta \gamma -\left(\beta ^{2}+\gamma ^{2}-a^{2} \right) \right]=\frac{1}{16}\left[4\beta ^{2}\gamma ^{2}-\left(\beta ^{2}+\gamma ^{2}-a^{2} \right)^{2} \right] \displaystyle\frac{1}{16}\left[2\beta \gamma +\left(\beta ^{2}+\gamma ^{2}-a^{2} \right) \right]\left[2\beta \gamma -\left(\beta ^{2}+\gamma ^{2}-a^{2} \right) \right]=\frac{1}{16}\left[4\beta ^{2}\gamma ^{2}-\left(\beta ^{2}+\gamma ^{2}-a^{2} \right)^{2} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/2faeb3b8926f1a099c716ffcd885fcc5.png)
![\displaystyle E^{2}=\frac{1}{16}\left[4\left(x^{2}+y^{2}+xy \right)\left(x^{2}+z^{2}+xz \right)-\left(2x^{2}+xz+xy-yz \right)^{2} \right] \displaystyle E^{2}=\frac{1}{16}\left[4\left(x^{2}+y^{2}+xy \right)\left(x^{2}+z^{2}+xz \right)-\left(2x^{2}+xz+xy-yz \right)^{2} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/aae3d7f5e473fb3ebf7a76de7ef6d82f.png)


![4\left[x^{2}+\left(z^{2}+xz \right) \right]\left[x^{2}+\left(y^{2}+xy \right) \right]-\left[2x^{2}+\left(xz+xy-yz \right) \right]^{2}= 4\left[x^{2}+\left(z^{2}+xz \right) \right]\left[x^{2}+\left(y^{2}+xy \right) \right]-\left[2x^{2}+\left(xz+xy-yz \right) \right]^{2}=](/forum/ext/geomar/texintegr/latexrender/pictures/b1c0b058b9c0c52f5e188c90a217ed52.png)





 από όπου συμπεραίνουμε ότι
από όπου συμπεραίνουμε ότι