parmenides51 έγραψε:Εξεταστές: Συμόπουλος - Λαδόπουλος
1. Δίνεται τρίγωνο

εγγεγραμμένο σε τρίγωνο

(το

βρίσκεται στην

,το

βρίσκεται στην

, το

βρίσκεται στην

). Να δείξετε οτι για να έχουν τα τρίγωνα κοινό κέντρου βάρους πρέπει και αρκεί να ισχύει η σχέση

.
Αυτό το μάλλον κλασσικό θέμα θα λυθεί με διανύσματα , έξω από τα εξεταστικά πλαίσια του 1963.Νομίζω ότι πρόκειται για μια χαρακτηριστική περίπτωση για το πώς ένα θέμα Ευκλείδειας Γεωμετρίας αντιμετωπίζεται πολύ πετυχημένα με διανύσματα.
Θα βασιστούμε στην άσκηση 7 της σελίδας 29 του τρέχοντος σχολικού βιβλίου Μαθηματικών Κατεύθυνσης της Β' Λυκείου.
Η άσκηση είναι η εξής:
Αν  και
και  είναι τα βαρύκεντρα δύο τριγώνων
είναι τα βαρύκεντρα δύο τριγώνων  και
και  , να αποδείξετε ότι
, να αποδείξετε ότι

Δε γράφω λύση της άσκησης αυτής , τη θεωρώ πολύ απλή.
Θα αποδείξουμε πρώτα ότι :
Δίνεται τρίγωνο

εγγεγραμμένο σε τρίγωνο

(το

βρίσκεται στην

,το

βρίσκεται στην

, το

βρίσκεται στην

). Αν

τότε τα τρίγωνα αυτά έχουν κοινό κέντρο βάρους.
ΑΠΟΔΕΙΞΗ
Θέτουμε ότι

Ισχύει ότι

δηλαδή

Για να περάσουμε στη διανυσματική διατύπωση , ισχύει ότι



Συνεπώς έχουμε
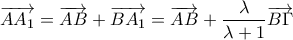

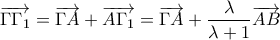
Αν προστεθούν κατά μέλη οι τρεις τελευταίες ισότητες έχουμε

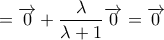
Έτσι λοιπόν , αν

τα βαρύκεντρα των τριγώνων

, ισχύει ότι
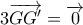
και συνεπώς

Αυτό σημαίνει ότι τα

ταυτίζονται.
Όποιος έχει κοιτάξει κάπως επισταμένα τα βιβλία Ευκλείδειας Γεωμετρίας που κυκλοφόρησαν τη δεκαετία του 1970 , έχει δει αποδείξεις της παραπάνω πρότασης.
Ας δούμε τώρα την αντίστροφη πρόταση:
Δίνεται τρίγωνο

εγγεγραμμένο σε τρίγωνο

(το

βρίσκεται στην

,το

βρίσκεται στην

, το

βρίσκεται στην

). Αν τα τρίγωνα αυτά έχουν κοινό κέντρο βάρους τότε

.
ΑΠΟΔΕΙΞΗ
Θέτω


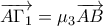
Αυτό που θα αποδειχθεί είναι ότι

Φυσικά

δηλαδή

δηλαδή

δηλαδή

δηλαδή

δηλαδή
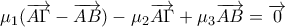
δηλαδή
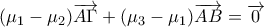
και αφού τα

είναι γραμμικώς ανεξάρτητα , έπεται ότι
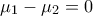
και

Από αυτές τις δυο τελευταίες βρίσκεται ότι
 Η ουσία της απόδειξης τελειώνει εδώ. Τα υπόλοιπα νομίζω ότι είναι θέμα ρουτίνας...
Νομίζω ότι αξίζει να γράψω λίγα για τον έναν από τους δύο ανθρώπους που έβαλαν αυτά τα θέματα , τον Παναγιώτη Λαδόπουλο. Γεννήθηκε στον Πειραιά το 1914 και πέθανε το 2005. Σπούδασε πολιτικός μηχανικός και κατόπιν μαθηματικά. Το 1947 αναγορεύτηκε διδάκτορας στα Μαθηματικά. Από το 1956 δίδαξε Παραστατική Γεωμετρία στο ΑΠΘ και από το 1965 έως το 1981 δίδαξε στο ΕΜΠ. Τα βιβλία του ''Παραστατική Γεωμετρία'' και ''Στοιχεία Προβολικής Γεωμετρίας I '' και '' Στοιχεία Προβολικής Γεωμετρίας ΙI '' είναι κλασσικά.
Η ουσία της απόδειξης τελειώνει εδώ. Τα υπόλοιπα νομίζω ότι είναι θέμα ρουτίνας...
Νομίζω ότι αξίζει να γράψω λίγα για τον έναν από τους δύο ανθρώπους που έβαλαν αυτά τα θέματα , τον Παναγιώτη Λαδόπουλο. Γεννήθηκε στον Πειραιά το 1914 και πέθανε το 2005. Σπούδασε πολιτικός μηχανικός και κατόπιν μαθηματικά. Το 1947 αναγορεύτηκε διδάκτορας στα Μαθηματικά. Από το 1956 δίδαξε Παραστατική Γεωμετρία στο ΑΠΘ και από το 1965 έως το 1981 δίδαξε στο ΕΜΠ. Τα βιβλία του ''Παραστατική Γεωμετρία'' και ''Στοιχεία Προβολικής Γεωμετρίας I '' και '' Στοιχεία Προβολικής Γεωμετρίας ΙI '' είναι κλασσικά. εγγεγραμμένο σε τρίγωνο
εγγεγραμμένο σε τρίγωνο  (το
(το  βρίσκεται στην
βρίσκεται στην  ,το
,το  βρίσκεται στην
βρίσκεται στην  , το
, το  βρίσκεται στην
βρίσκεται στην  ). Να δείξετε οτι για να έχουν τα τρίγωνα κοινό κέντρου βάρους πρέπει και αρκεί να ισχύει η σχέση
). Να δείξετε οτι για να έχουν τα τρίγωνα κοινό κέντρου βάρους πρέπει και αρκεί να ισχύει η σχέση  .
. και σημείο
και σημείο  εκτός αυτής. Φέρνουμε από το
εκτός αυτής. Φέρνουμε από το  μια τυχαία ευθεία που τέμνει την
μια τυχαία ευθεία που τέμνει την  στο
στο  . Με πλευρά την
. Με πλευρά την  κατασκευάζουμε ισοσκελές ορθογώνιο τρίγωνο
κατασκευάζουμε ισοσκελές ορθογώνιο τρίγωνο  (
( ). Να βρεθεί ο γεωμετρικός τόπος του εγγεγραμμένου κύκλου στο
). Να βρεθεί ο γεωμετρικός τόπος του εγγεγραμμένου κύκλου στο  .
. . Να αποδειχθεί οτι το τετράγωνο της επιφάνειας της σφαίρας, που βρίσκεται εσωτερικά της στερεάς γωνίας ισούται με το άθροισμα των τετραγώνων των επιφανειών της σφαίρας που βρίσκονται εξωτερικά της τρίεδρης γωνίας.
. Να αποδειχθεί οτι το τετράγωνο της επιφάνειας της σφαίρας, που βρίσκεται εσωτερικά της στερεάς γωνίας ισούται με το άθροισμα των τετραγώνων των επιφανειών της σφαίρας που βρίσκονται εξωτερικά της τρίεδρης γωνίας.
 και
και  είναι τα βαρύκεντρα δύο τριγώνων
είναι τα βαρύκεντρα δύο τριγώνων  και
και  , να αποδείξετε ότι
, να αποδείξετε ότι 






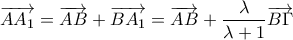

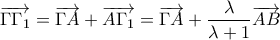

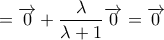
 τα βαρύκεντρα των τριγώνων
τα βαρύκεντρα των τριγώνων  , ισχύει ότι
, ισχύει ότι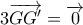



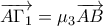






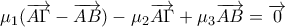
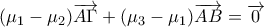
 είναι γραμμικώς ανεξάρτητα , έπεται ότι
είναι γραμμικώς ανεξάρτητα , έπεται ότι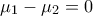 και
και 