- ThemataAG-4.pdf
- (89.37 KiB) Μεταφορτώθηκε 275 φορές
ΘΕΜΑΤΑ ΑΛΓΕΒΡΙΚΗΣ ΓΕΩΜΕΤΡΙΑΣ
- nsmavrogiannis
- Επιμελητής
- Δημοσιεύσεις: 4455
- Εγγραφή: Σάβ Δεκ 20, 2008 7:13 pm
- Τοποθεσία: Αθήνα
- Επικοινωνία:
Re: ΘΕΜΑΤΑ ΑΛΓΕΒΡΙΚΗΣ ΓΕΩΜΕΤΡΙΑΣ
Ευχαριστούμε. Αλλά σε ποιο πανεπιστήμιο ήσαν θέματα;
Αν κανείς δεν ελπίζει, δεν θα βρεί το ανέλπιστο, οι δρόμοι για το ανεξερεύνητο θα είναι κλειστοί.
Ηράκλειτος
Ηράκλειτος
Re: ΘΕΜΑΤΑ ΑΛΓΕΒΡΙΚΗΣ ΓΕΩΜΕΤΡΙΑΣ
ΘΕΜΑ 1
1. Θεωρία : Μπορείς να βρεις την απάντηση σε κάθε σχετικό βιβλίο. Χρησιμοποιείται ο επιμορφισμός
![\displaystyle{\mathbb{K}[x_1,...,x_n]\to \mathbb{K}\,\,,f(x_1,...,x_n)\mapsto f(a_1,...,a_n)} \displaystyle{\mathbb{K}[x_1,...,x_n]\to \mathbb{K}\,\,,f(x_1,...,x_n)\mapsto f(a_1,...,a_n)}](/forum/ext/geomar/texintegr/latexrender/pictures/c13e63da58716f74af00725eb748678e.png) .
.
2. Αν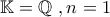 (όχι αλγεβρικά κλειστό), τότε το
(όχι αλγεβρικά κλειστό), τότε το 
είναι μέγιστο, αλλά όχι της μορφής για κάποιο
για κάποιο  .
.
3. Όχι, στον δακτύλιο , το
, το  είναι πρώτο αλλά, όχι μέγιστο ιδέωδες.
είναι πρώτο αλλά, όχι μέγιστο ιδέωδες.
4. Θα αποδειχθεί κάτι πιο γενικό : Σε μια περιοχή κύριων ιδεωδών, κάθε μη μηδενικό πρώτο ιδεώδες είναι και μέγιστο (και αυτό το βρίσκεις αλλά το γράφω)
Απόδειξη
Έστω μια περιοχή κύριων ιδεωδών και ας είναι
μια περιοχή κύριων ιδεωδών και ας είναι  πρώτο ιδεώδες .
πρώτο ιδεώδες .
Έστω . Τότε,
. Τότε,
 και άρα
και άρα  με
με  πρώτο.
πρώτο.
Συνεπώς, ή
ή  . Αν
. Αν  , τότε
, τότε  ,
,
οπότε .
.
Αν , τότε
, τότε  .
.
Εν τέλει, το είναι μέγιστο.
είναι μέγιστο.
1. Θεωρία : Μπορείς να βρεις την απάντηση σε κάθε σχετικό βιβλίο. Χρησιμοποιείται ο επιμορφισμός
![\displaystyle{\mathbb{K}[x_1,...,x_n]\to \mathbb{K}\,\,,f(x_1,...,x_n)\mapsto f(a_1,...,a_n)} \displaystyle{\mathbb{K}[x_1,...,x_n]\to \mathbb{K}\,\,,f(x_1,...,x_n)\mapsto f(a_1,...,a_n)}](/forum/ext/geomar/texintegr/latexrender/pictures/c13e63da58716f74af00725eb748678e.png) .
.2. Αν
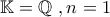 (όχι αλγεβρικά κλειστό), τότε το
(όχι αλγεβρικά κλειστό), τότε το 
είναι μέγιστο, αλλά όχι της μορφής
 για κάποιο
για κάποιο  .
.3. Όχι, στον δακτύλιο
 , το
, το  είναι πρώτο αλλά, όχι μέγιστο ιδέωδες.
είναι πρώτο αλλά, όχι μέγιστο ιδέωδες.4. Θα αποδειχθεί κάτι πιο γενικό : Σε μια περιοχή κύριων ιδεωδών, κάθε μη μηδενικό πρώτο ιδεώδες είναι και μέγιστο (και αυτό το βρίσκεις αλλά το γράφω)
Απόδειξη
Έστω
 μια περιοχή κύριων ιδεωδών και ας είναι
μια περιοχή κύριων ιδεωδών και ας είναι  πρώτο ιδεώδες .
πρώτο ιδεώδες .Έστω
 . Τότε,
. Τότε, και άρα
και άρα  με
με  πρώτο.
πρώτο.Συνεπώς,
 ή
ή  . Αν
. Αν  , τότε
, τότε  ,
,οπότε
 .
.Αν
 , τότε
, τότε  .
.Εν τέλει, το
 είναι μέγιστο.
είναι μέγιστο.Παπαπέτρος Ευάγγελος
Re: ΘΕΜΑΤΑ ΑΛΓΕΒΡΙΚΗΣ ΓΕΩΜΕΤΡΙΑΣ
ΘΕΜΑ 2
1,2.
Το είναι το σύνολο των πρώτων ιδεωδών του
είναι το σύνολο των πρώτων ιδεωδών του  και τα κλειστά της τοπολογίας
και τα κλειστά της τοπολογίας
 είναι τα
είναι τα  , όπου
, όπου
 .
.
Μπορείς να αποδείξεις ότι αν είναι ιδεώδη, τότε
είναι ιδεώδη, τότε

1,2.
Το
 είναι το σύνολο των πρώτων ιδεωδών του
είναι το σύνολο των πρώτων ιδεωδών του  και τα κλειστά της τοπολογίας
και τα κλειστά της τοπολογίας  είναι τα
είναι τα  , όπου
, όπου .
.Μπορείς να αποδείξεις ότι αν
 είναι ιδεώδη, τότε
είναι ιδεώδη, τότε
Παπαπέτρος Ευάγγελος
Re: ΘΕΜΑΤΑ ΑΛΓΕΒΡΙΚΗΣ ΓΕΩΜΕΤΡΙΑΣ
ΘΕΜΑ 3
1.
Αρχικά, υπάρχει μέγιστο ιδεώδες, άρα πρώτο, που περιέχει το ιδεώδες , οπότε
, οπότε
 . Αν
. Αν  , τότε υπάρχει
, τότε υπάρχει
 τέτοιο, ώστε
τέτοιο, ώστε  , δηλαδή
, δηλαδή 
για κάποιο . Αν λοιπόν
. Αν λοιπόν 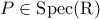 με
με  , τότε
, τότε
 . Ώστε,
. Ώστε,
 .
.
Απ' την άλλη, έστω

και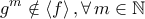 .
.
Έστω και από υπόθεση
και από υπόθεση 
διότι . Επειδή θα χρησιμοποιηθεί το λήμμα του Zorn, γράφω αναλυτικά.
. Επειδή θα χρησιμοποιηθεί το λήμμα του Zorn, γράφω αναλυτικά.
Το μη κενό σύνολο είναι μερικώς διατεταγμένο από τη σχέση του "υποσυνόλου" .
είναι μερικώς διατεταγμένο από τη σχέση του "υποσυνόλου" .
Έστω ένα ολικώς διατεταγμένο υποσύνολό του. Θέτουμε
ένα ολικώς διατεταγμένο υποσύνολό του. Θέτουμε  , όπου λόγω
, όπου λόγω
ολικής διάταξης, το είναι ιδεώδες και
είναι ιδεώδες και 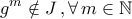 .
.
Άρα, . Επιπλέον,
. Επιπλέον,  και έτσι, το
και έτσι, το 
είναι άνω φράγμα του στο
στο  .
.
Από το λήμμα του Zorn, το έχει μεγιστικό στοιχείο, έστω
έχει μεγιστικό στοιχείο, έστω  .
.
Ας είναι τέτοια, ώστε
τέτοια, ώστε  αλλά
αλλά  .
.
Έτσι, (αφού το
(αφού το  είναι μεγιστικό) και συνεπώς
είναι μεγιστικό) και συνεπώς
υπάρχουν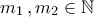 με
με 
δηλαδή . Τότε,
. Τότε,
 , άτοπο διότι
, άτοπο διότι  .
.
Άρα πρώτο ιδεώδες με
πρώτο ιδεώδες με  , άτοπο και πάλι αφού
, άτοπο και πάλι αφού
 .
.
Εν τέλει,
1.
Αρχικά, υπάρχει μέγιστο ιδεώδες, άρα πρώτο, που περιέχει το ιδεώδες
 , οπότε
, οπότε . Αν
. Αν  , τότε υπάρχει
, τότε υπάρχει τέτοιο, ώστε
τέτοιο, ώστε  , δηλαδή
, δηλαδή 
για κάποιο
 . Αν λοιπόν
. Αν λοιπόν 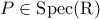 με
με  , τότε
, τότε . Ώστε,
. Ώστε,  .
.Απ' την άλλη, έστω

και
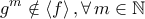 .
.Έστω
 και από υπόθεση
και από υπόθεση 
διότι
 . Επειδή θα χρησιμοποιηθεί το λήμμα του Zorn, γράφω αναλυτικά.
. Επειδή θα χρησιμοποιηθεί το λήμμα του Zorn, γράφω αναλυτικά.Το μη κενό σύνολο
 είναι μερικώς διατεταγμένο από τη σχέση του "υποσυνόλου" .
είναι μερικώς διατεταγμένο από τη σχέση του "υποσυνόλου" .Έστω
 ένα ολικώς διατεταγμένο υποσύνολό του. Θέτουμε
ένα ολικώς διατεταγμένο υποσύνολό του. Θέτουμε  , όπου λόγω
, όπου λόγω ολικής διάταξης, το
 είναι ιδεώδες και
είναι ιδεώδες και 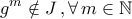 .
.Άρα,
 . Επιπλέον,
. Επιπλέον,  και έτσι, το
και έτσι, το 
είναι άνω φράγμα του
 στο
στο  .
.Από το λήμμα του Zorn, το
 έχει μεγιστικό στοιχείο, έστω
έχει μεγιστικό στοιχείο, έστω  .
.Ας είναι
 τέτοια, ώστε
τέτοια, ώστε  αλλά
αλλά  .
.Έτσι,
 (αφού το
(αφού το  είναι μεγιστικό) και συνεπώς
είναι μεγιστικό) και συνεπώςυπάρχουν
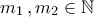 με
με 
δηλαδή
 . Τότε,
. Τότε, , άτοπο διότι
, άτοπο διότι  .
.Άρα
 πρώτο ιδεώδες με
πρώτο ιδεώδες με  , άτοπο και πάλι αφού
, άτοπο και πάλι αφού  .
.Εν τέλει,

Παπαπέτρος Ευάγγελος
Re: ΘΕΜΑΤΑ ΑΛΓΕΒΡΙΚΗΣ ΓΕΩΜΕΤΡΙΑΣ
ΘΕΜΑ 4
4. Κλασική κατασκευή και έχουμε ότι
 .
.
(το έγραψα αμέσως διότι υπάρχει σε όλα τα βιβλία)
Βάσει αυτού, θα λύσουμε και το τέταρτο ερώτημα του 3ου θέματος.
Υποθέτουμε ότι το είναι μηδενοδύναμο, δηλαδή
είναι μηδενοδύναμο, δηλαδή  για κάποιο
για κάποιο  .
.
Εδώ έχουμε .
.
Έστω . Τότε, υπάρχει πρώτο ιδεώδες
. Τότε, υπάρχει πρώτο ιδεώδες  του
του 
με και
και  είναι πρώτο ιδέωδες του
είναι πρώτο ιδέωδες του  .
.
Όμως, από το πρώτο ερώτημα έχουμε,
 ,
,
δηλαδή, , άτοπο.
, άτοπο.
Αλλιώς υπάρχει η ακόλουθη πρόταση :
 αν, και μόνο αν, το
αν, και μόνο αν, το  περιέχει ένα μηδενοδύναμο στοιχείο.
περιέχει ένα μηδενοδύναμο στοιχείο.
4. Κλασική κατασκευή και έχουμε ότι
 .
.(το έγραψα αμέσως διότι υπάρχει σε όλα τα βιβλία)
Βάσει αυτού, θα λύσουμε και το τέταρτο ερώτημα του 3ου θέματος.
Υποθέτουμε ότι το
 είναι μηδενοδύναμο, δηλαδή
είναι μηδενοδύναμο, δηλαδή  για κάποιο
για κάποιο  .
.Εδώ έχουμε
 .
.Έστω
 . Τότε, υπάρχει πρώτο ιδεώδες
. Τότε, υπάρχει πρώτο ιδεώδες  του
του 
με
 και
και  είναι πρώτο ιδέωδες του
είναι πρώτο ιδέωδες του  .
.Όμως, από το πρώτο ερώτημα έχουμε,
 ,
,δηλαδή,
 , άτοπο.
, άτοπο.Αλλιώς υπάρχει η ακόλουθη πρόταση :
 αν, και μόνο αν, το
αν, και μόνο αν, το  περιέχει ένα μηδενοδύναμο στοιχείο.
περιέχει ένα μηδενοδύναμο στοιχείο.Παπαπέτρος Ευάγγελος
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης
