Θέμα Εισαγωγικών Scuola Normale Superiore 2014-15 (1)

dement · #1

Να βρεθούν όλες οι τριάδες θετικών ακεραίων a, b, c

που ικανοποιούν την εξίσωση

a^7 + b^7 = 7^c

harrisp · #2

Απο το θεωρημα Zsigmondy το a^7+b^7

εχει τουλάχιστον

πρώτους διαιρέτες, άτοπο αφου 7 πρωτος.

Η Επίλυση του a^p+b^p=q^c

,

πρωτοι ακολουθεί ακριβώς την ίδια τακτική.

dement · #3

(Ο

, αν δεν κάνω λάθος, αρκεί να είναι περιττός.)

harrisp · #4

Ναι έχετε δίκιο.

#5

ΧΑΡΗΣ ΤΙΟΥΡΙΝΓΚ έγραψε:Απο το θεωρημα Zsigmondy το εχει τουλάχιστον πρώτους διαιρέτες, άτοπο αφου 7 πρωτος.

Η Επίλυση του , πρωτοι ακολουθεί ακριβώς την ίδια τακτική.

Αυτό το θεώρημα -- ωραία περίπτωση οι 4 αδελφοί Zsigmondy, αναζητήστε τους στο διαδίκτυο -- αναμένεται να είναι γνωστό στους εξεταζόμενους ή θεωρείται αρκετά ρεαλιστική η απόδειξη (του) κατά την διάρκεια της εξέτασης χωρίς προηγούμενη γνώση του; Νομίζω ότι η ανεξάρτητη από το Θεώρημα Zsigmondy απόδειξη που δίνω παρακάτω είναι αρκετά απλή:

Θέτουμε a+b=7^d

, οπότε από την $a^6-a^5b+a^4b^2-a^3b^3+a^2b^4-ab^5+b^6=7^{c-d}$ προκύπτει η

$7^d(7^{5d}-13\cdot7^{4d}a+27\cdot7^{3d}a^2-41\cdot7^{2d}a^3+35\cdot7^da^4-21a^5)+7a^6=7^{c-d},$

απ' όπου εύκολα συνάγεται, λόγω $d\geq1$ , ότι 7^2|7a^6

(άτοπο) ... εκτός και αν c-d=1

(αδύνατο).

Συμπεραίνουμε ότι η αρχική εξίσωση δεν έχει ακέραιες λύσεις.

#6

Η παραπάνω μέθοδος δίνει την εξής γενίκευση (που ήδη αναφέρθηκε):

Θεώρημα: Αν

,

φυσικοί,

πρώτος και

περιττός τότε οι μόνες λύσεις της a^p+b^p=q^c

στους φυσικούς είναι οι a=1, b=2, q=3, p=3

και

.

Απόδειξη: με διαδοχική αναγωγή στις (I) a^q+b^q=q^c

και (II) $a^q+b^q\leq (a+b)^2$ .

(I) Εύλογα υποθέτουμε ότι οι

,

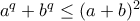δεν διαιρούνται δια

, και θέτουμε a+b=q^d

, όπου

. Αντικαθιστώντας την b=q^d-a

στην $(a+b)(a^{p-1}-a^{p-2}b+...-ab^{p-2}+b^{p-1})=q^c$ προκύπτει η ισότητα

$pa^{p-1}+Mq^d=q^{c-d},$ όπου

ακέραιος,

από την οποία συμπεραίνουμε ότι q|p

. Θέτοντας p=mq

, η

δίνει

, όπου

,

.

(II) Αντικαθιστώντας, και πάλι, την b=q^d-a

στην $(a+b)(a^{q-1}-a^{q-2}b+...-ab^{q-2}+b^{q-1})=q^c$ , λαμβάνουμε διαδοχικά τις ισότητες

$qa^{q-1}-[1+...+(q-2)+(q-1)]a^{q-2}q^d+Nq^{2d}=q^{c-d},$ όπου

ακέραιος, και

$a^{q-1}-\displaystyle\frac{q+1}{2}a^{q-2}q^d+Nq^{2d-1}=q^{c-d-1}.$

Επειδή $d\leq 2d-1$ , αν ίσχυε και η $d\leq c-d-1$ ... ο q^d

θα διαιρούσε τον $a^{q-1}$ , άτοπο. Ισχύει λοιπόν η ανισότητα d>c-d-1

, άρα και η $c\leq2d$ . Αυτό όμως σημαίνει, λόγω των a^q+b^q=q^c

και

, ότι ισχύει και η ανισότητα

$a^q+b^q\leq(a+b)^2$ .

Η ανισότητα αυτή δεν ισχύει για $q\geq4$ , εκτός και αν a=b=1

. Πράγματι, αν a>1

και

τότε προφανώς $a^4+b^4>a^3+b^3\geq 2a^2+2b^2\geq(a+b)^2$ . Αν πάλι a=1

και

, τότε

, άρα

.

Για

... έχουμε ήδη δείξει παραπάνω ότι η ανισότητα μπορεί να ισχύει μόνο αν a=1

(ή

). Παρατηρούμε ότι η $1+b^3\leq(1+b)^2$ είναι ισοδύναμη προς την $(b-2)(b+1)\geq0$ , ισχύει επομένως μόνο για b=2

. Και πράγματι για a=1

,

, η

ισχύει.

[Η παραπάνω απόδειξη δεν είναι καθοριστικά δυσκολότερη από την απόδειξη της ειδικής περίπτωσης που δόθηκε ως θέμα.]

Θέμα Εισαγωγικών Scuola Normale Superiore 2014-15 (1)

Θέμα Εισαγωγικών Scuola Normale Superiore 2014-15 (1)

Re: Θέμα Εισαγωγικών Scuola Normale Superiore 2014-15 (1)

Re: Θέμα Εισαγωγικών Scuola Normale Superiore 2014-15 (1)

Re: Θέμα Εισαγωγικών Scuola Normale Superiore 2014-15 (1)

Re: Θέμα Εισαγωγικών Scuola Normale Superiore 2014-15 (1)

Re: Θέμα Εισαγωγικών Scuola Normale Superiore 2014-15 (1)

Μέλη σε σύνδεση