ΠΡΟΒΛΗΜΑ 1
Πρέπει να προγραμματίσετε τη λειτουργία μίας μηχανής που χρησιμοποιείται στη βιομηχανική παραγωγή πλακακιών για πατώματα. Τα πλακάκια είναι σχήματος τετραγώνου και τα βήματα της διαδικασίας είναι τα ακόλουθα:
- Επιλέγεται μία συνάρτηση
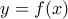 συνεχής στο
συνεχής στο ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) που ικανοποιεί τις συνθήκες:
που ικανοποιεί τις συνθήκες:(α)

(β)

(γ)
 για
για 
- Η μηχανή διαγράφει το γράφημα
 της συνάρτησης
της συνάρτησης 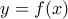 καθώς και τα συμμετρικά του ως προς τον άξονα
καθώς και τα συμμετρικά του ως προς τον άξονα  , τον άξονα
, τον άξονα  και την τομή των αξόνων
και την τομή των αξόνων  , σχηματίζοντας έτσι μία κλειστή καμπύλη
, σχηματίζοντας έτσι μία κλειστή καμπύλη 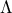 που διέρχεται από τα σημεία
που διέρχεται από τα σημεία 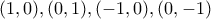 , συμμετρική ως προς τους καρτεσιανούς άξονες και την τομή τους και περιεχόμενη στο τετράγωνο
, συμμετρική ως προς τους καρτεσιανούς άξονες και την τομή τους και περιεχόμενη στο τετράγωνο  με κορυφές τα σημεία
με κορυφές τα σημεία  .
. - Η μηχανή κατασκευάζει το πλακάκι χρωματίζοντας το εσωτερικό της κλειστής καμπύλης
 και αφήνοντας λευκό το υπόλοιπο του τετραγώνου
και αφήνοντας λευκό το υπόλοιπο του τετραγώνου  .
. Το εγχειρίδιο οδηγιών χρήσης δίνει ένα παράδειγμα κατασκευής ενός απλού πλακακιού: 1. Με αναφορά στο παράδειγμα, δώστε τον τύπο της συνάρτησης
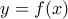 και της κλειστής καμπύλης
και της κλειστής καμπύλης 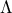 , ώστε να μπορέσει να γίνει μία δοκιμή της σωστής λειτουργίας της μηχανής.
, ώστε να μπορέσει να γίνει μία δοκιμή της σωστής λειτουργίας της μηχανής.Σας ζητείται να κατασκευάσετε ένα πλακάκι με ένα σχέδιο πιο λεπτομερές το οποίο, εκτός από τις τρεις προαναφερθείσες συνθήκες, ικανοποιεί και την
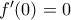 και το εμβαδόν της χρωματισμένης επιφάνειας ισούται με το
και το εμβαδόν της χρωματισμένης επιφάνειας ισούται με το  του συνολικού εμβαδού του πλακακιού. Για αυτόν τον σκοπό, θεωρήστε πολυωνυμικές συναρτήσεις δευτέρου και τρίτου βαθμού.
του συνολικού εμβαδού του πλακακιού. Για αυτόν τον σκοπό, θεωρήστε πολυωνυμικές συναρτήσεις δευτέρου και τρίτου βαθμού.2. Αφού αποδείξετε ότι δεν είναι δυνατόν να ικανοποιηθούν οι συνθήκες με πολυωνυμική συνάρτηση δευτέρου βαθμού, προσδιορίστε τους συντελεστές
 της πολυωνυμικής συνάρτησης τρίτου βαθμού που ικανοποιεί τις συνθήκες. Αναπαραστήστε στη συνέχεια στο καρτεσιανό επίπεδο το πλακάκι που προκύπτει.
της πολυωνυμικής συνάρτησης τρίτου βαθμού που ικανοποιεί τις συνθήκες. Αναπαραστήστε στη συνέχεια στο καρτεσιανό επίπεδο το πλακάκι που προκύπτει.Σε έναν πελάτη προτείνονται δύο διαφορετικά σχέδια, που προκύπτουν από τις συναρτήσεις
 ,
,  , στο διάστημα
, στο διάστημα ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) και με
και με  θετικό ακέραιο.
θετικό ακέραιο.3. Αποδείξτε ότι, για κάθε
 , όλες αυτές οι συναρτήσεις ικανοποιούν τις προαναφερθείσες συνθήκες (α), (β), (γ). Ορίζοντας
, όλες αυτές οι συναρτήσεις ικανοποιούν τις προαναφερθείσες συνθήκες (α), (β), (γ). Ορίζοντας  τα εμβαδά των χρωματισμένων περιοχών των πλακακιών που προκύπτουν αντίστοιχα από τις συναρτήσεις
τα εμβαδά των χρωματισμένων περιοχών των πλακακιών που προκύπτουν αντίστοιχα από τις συναρτήσεις  , υπολογίστε τα
, υπολογίστε τα  και ερμηνεύστε γεωμετρικά το αποτέλεσμα.
και ερμηνεύστε γεωμετρικά το αποτέλεσμα.Ο πελάτης αποφασίζει να παραγγείλει
 πλακάκια με το σχέδιο
πλακάκια με το σχέδιο  και
και  πλακάκια με το σχέδιο
πλακάκια με το σχέδιο 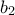 . Ο χρωματισμός γίνεται με έναν μηχανικό βραχίονα ο οποίος, αφού τελειώσει τον χρωματισμό, επανέρχεται στην αρχική του θέση διασχίζοντας μια διαγώνιο του πλακακιού. Λόγω μίας βλάβης, κατά την παραγωγή των
. Ο χρωματισμός γίνεται με έναν μηχανικό βραχίονα ο οποίος, αφού τελειώσει τον χρωματισμό, επανέρχεται στην αρχική του θέση διασχίζοντας μια διαγώνιο του πλακακιού. Λόγω μίας βλάβης, κατά την παραγωγή των 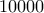 πλακακιών, υπάρχει μια πιθανότητα
πλακακιών, υπάρχει μια πιθανότητα  ο βραχίονας να αφήσει να πέσει μία σταγόνα χρώματος σε ένα τυχαίο σημείο επί της διαγωνίου, λεκιάζοντας το πλακάκι.
ο βραχίονας να αφήσει να πέσει μία σταγόνα χρώματος σε ένα τυχαίο σημείο επί της διαγωνίου, λεκιάζοντας το πλακάκι.4. Υπολογίστε χονδρικά, δικαιολογώντας την απάντησή σας, τον αριθμό των πλακακιών που θα έχουν σταγόνα χρώματος στη λευκή περιοχή τους και, κατά συνέπεια, θα πρέπει να απορριφθούν από την παραγωγή.

![\displaystyle [0,1] \displaystyle [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/3c768608c76c88b7847dbf1ec30ec3d4.png) καταλήγουμε στην
καταλήγουμε στην ![\displaystyle f(x)=1-x,x\in [0,1] \displaystyle f(x)=1-x,x\in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/7c090b09e1ed8dd1d1461d1c3de57f92.png)
![\displaystyle x\in [0,1] \displaystyle x\in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ebfe1b7a80ef118488d36735091887dd.png) και
και 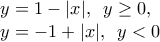
 , τότε :
, τότε : ,
,  ,
, 
![\displaystyle f(x)=-{{x}^{2}}+1\ge 0,x\in [0,1] \displaystyle f(x)=-{{x}^{2}}+1\ge 0,x\in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/807a7192fcf8b3bce3f7196fce31a2ca.png)
![\displaystyle \int\limits_0^1 {( - {x^2} + 1)dx = \left[ {\frac{{ - {x^3}}}{3} + x} \right]_0^1} = \frac{2}{3} > 0,55 \displaystyle \int\limits_0^1 {( - {x^2} + 1)dx = \left[ {\frac{{ - {x^3}}}{3} + x} \right]_0^1} = \frac{2}{3} > 0,55](/forum/ext/geomar/texintegr/latexrender/pictures/488a1ad83fb345132a1fefbe1b6f4459.png) ,
, 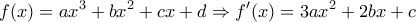 , τότε :
, τότε : ,
,  ,
, 
![\displaystyle f(x)=a{{x}^{3}}-(a+1){{x}^{2}}+1\ge 0,x\in [0,1] \displaystyle f(x)=a{{x}^{3}}-(a+1){{x}^{2}}+1\ge 0,x\in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/1f9242c38a55e631977d29b35fd6ebc9.png)

 , οπότε:
, οπότε: 

 . Τότε :
. Τότε : 

 . Τότε :
. Τότε : 

![\displaystyle \int\limits_0^1 {(1 - {x^n}} )dx = \left[ {x - \frac{{{x^{n + 1}}}}{{n + 1}}} \right]_0^1 = 1 - \frac{1}{{n + 1}} \displaystyle \int\limits_0^1 {(1 - {x^n}} )dx = \left[ {x - \frac{{{x^{n + 1}}}}{{n + 1}}} \right]_0^1 = 1 - \frac{1}{{n + 1}}](/forum/ext/geomar/texintegr/latexrender/pictures/bc36c8ae199db9e68eaae7f0270119b7.png)

![\displaystyle \int\limits_0^1 {(1 - x} {)^n}dx = \left[ {\frac{{{{(1 - x)}^{n + 1}}}}{{ - n - 1}}} \right]_0^1 = \frac{1}{{n + 1}} \displaystyle \int\limits_0^1 {(1 - x} {)^n}dx = \left[ {\frac{{{{(1 - x)}^{n + 1}}}}{{ - n - 1}}} \right]_0^1 = \frac{1}{{n + 1}}](/forum/ext/geomar/texintegr/latexrender/pictures/99280c9d4d4dcec36c0ee4d7af4005b0.png) , άρα
, άρα 
 και
και 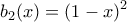 έχουν κέντρο συμμετρίας το σημείο
έχουν κέντρο συμμετρίας το σημείο 
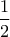 της διαγωνίου .
της διαγωνίου . για κάθε πλακάκι , έχουμε ότι η πιθανότητα για ελαττωματικό πλακάκι ,
για κάθε πλακάκι , έχουμε ότι η πιθανότητα για ελαττωματικό πλακάκι , 
 ελαττωματικά πλακάκια
ελαττωματικά πλακάκια