1. Να βρείτε τις πραγματικές λύσεις του συστήματος των εξισώσεων
![\displaystyle{\left\{\begin{matrix}
3\sqrt[3]{x^2y^5} = 4 \left (y^2-x^2) ,
\\
5\sqrt[3]{x^4y} = x^2+y^2 .
\end{matrix}\right.} \displaystyle{\left\{\begin{matrix}
3\sqrt[3]{x^2y^5} = 4 \left (y^2-x^2) ,
\\
5\sqrt[3]{x^4y} = x^2+y^2 .
\end{matrix}\right.}](/forum/ext/geomar/texintegr/latexrender/pictures/f22d4a60b13363695aaaa3653f091aec.png)
2. Να λύσετε την εξίσωση
 .
.3. Να λύσετε την ανίσωση
 .
.4. Το τρίγωνο
 είναι εγγεγραμμένο σε κύκλο
είναι εγγεγραμμένο σε κύκλο  ακτίνας
ακτίνας  και τα σημεία
και τα σημεία  ,
,  και
και  είναι τα μέσα των τμημάτων
είναι τα μέσα των τμημάτων  ,
,  και
και  αντίστοιχα. Οι κύκλοι
αντίστοιχα. Οι κύκλοι  ,
,  και
και  διέρχονται από τα σημεία
διέρχονται από τα σημεία  και
και  αντίστοιχα, εφάπτονται με τον κύκλο
αντίστοιχα, εφάπτονται με τον κύκλο  και ο καθένας έχει με το τρίγωνο
και ο καθένας έχει με το τρίγωνο  μοναδικό κοινό σημείο. Να βρείτε την ακτίνα του κύκλου
μοναδικό κοινό σημείο. Να βρείτε την ακτίνα του κύκλου  , αν οι ακτίνες των κύκλων
, αν οι ακτίνες των κύκλων  και
και  είναι ίσες με
είναι ίσες με  και
και 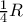 αντίστοιχα.
αντίστοιχα.5. Για κάθε τιμή της παραμέτρου
![a \in [0, \pi] a \in [0, \pi]](/forum/ext/geomar/texintegr/latexrender/pictures/77b5de5fb0d5a3b71e4d55c39c4f253b.png) να βρείτε την μέγιστη τιμή
να βρείτε την μέγιστη τιμή  της συνάρτησης
της συνάρτησης  στο σύνολο των σημείων
στο σύνολο των σημείων  τέτοιων, ώστε
τέτοιων, ώστε  . Να βρείτε τις τιμές της παραμέτρου
. Να βρείτε τις τιμές της παραμέτρου ![a \in [0, \pi] a \in [0, \pi]](/forum/ext/geomar/texintegr/latexrender/pictures/77b5de5fb0d5a3b71e4d55c39c4f253b.png) για τις οποίες η
για τις οποίες η  λαμβάνει την ελάχιστη τιμή της.
λαμβάνει την ελάχιστη τιμή της.6. Δίνεται τετράεδρο
 και σφαίρα που εφάπτεται των εδρών
και σφαίρα που εφάπτεται των εδρών  και
και  στα σημεία
στα σημεία  και
και  , που σποτελούν βάσεις υψών του τετράεδρου και τέμνει την ακμή
, που σποτελούν βάσεις υψών του τετράεδρου και τέμνει την ακμή  στα σημεία
στα σημεία  και
και  . Είναι γνωστό ότι
. Είναι γνωστό ότι  ,
,  ,
,  ,
,  . Να βρείτε την απόσταση μεταξύ των ακμών
. Να βρείτε την απόσταση μεταξύ των ακμών  και
και  , την ακτίνα του κύκλου που αποτελεί την τομή του επιπέδου
, την ακτίνα του κύκλου που αποτελεί την τομή του επιπέδου  με την σφαίρα και τον όγκο του τετράεδρου
με την σφαίρα και τον όγκο του τετράεδρου  .
.
 τότε
τότε  κ.λπ.
κ.λπ.

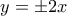 κ.λπ.
κ.λπ. στα
στα  αντίστοιχα.
αντίστοιχα.
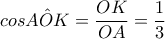
 προκύπτει ότι
προκύπτει ότι 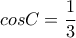


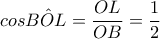
 προκύπτει ότι
προκύπτει ότι 
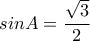
![cosB=cos\left [ 180^{0}-\left ( A+C \right ) \right ]=-cos\left ( A+C \right )=-\left ( cosAcosC-sinAsinC \right )= cosB=cos\left [ 180^{0}-\left ( A+C \right ) \right ]=-cos\left ( A+C \right )=-\left ( cosAcosC-sinAsinC \right )=](/forum/ext/geomar/texintegr/latexrender/pictures/b7384d624156682bff949fabd7904309.png)




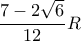
 του εγγεγραμμένου κύκλου του τριγώνου
του εγγεγραμμένου κύκλου του τριγώνου 



