Al.Koutsouridis έγραψε: ↑Δευ Ιούλ 26, 2021 10:08 pm
(1) Έστω

πολυώνυμο με πραγματικούς συντελεστές,

φυσικός αριθμός και

. Να αποδέιξετε ότι αν ισχύει η ταυτότητα

, τότε υπάρχει πολυώνυμο

τέτοιο, ώστε

.
(2) Λέμε ότι η

είναι ρητή συνάρτηση αν μπορεί να γραφεί στην μορφή

, όπου

πολυώνυμα με πραγματικούς συντελεστές. Να αποδείξετε ότι αν μια ρητή συνάρτηση

ικανοποιεί την ταυτότητα

, τότε υπάρχει ρητή συνάρτηση

τέτοια, ώστε

.
Λήμμα: Για κάθε φυσικό

το

εκφράζεται ως πολυώνυμο του

.
Πράγματι ειδικά για

έχουμε

, που είναι δευτεροβάθμιο πολυώνυμο του

.
Με ισχυρή επαγωγή τώρα, υποθέτοντας το ζητούμενο για όλα tα

έχουμε για το

ότι

,
όπως θέλαμε.
(1). Aν

τότε η υπόθεση

δίνει

που από το Λήμμα είναι άθροισμα πολυωνύμων του

, από όπου το ζητούμενο.
(2). Το (2) είναι βέβαια γενίκευση του (1) και μπορεί να λυθεί με χρήση του. Θα κάνω όμως ανεξάρτητη λύση μια και λύνεται με ουσιαστικά τον ίδιο τρόπο. Υποθέτω ότι το (1) μπήκε για να διευκολύνουν οι εξεταστές τον διαγωνιζόμενο, αλλά μπορούσε και να παραληφθεί.
Έχουμε
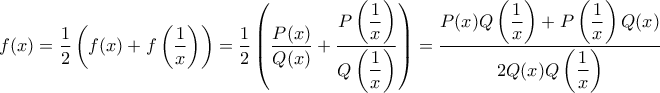
Κοιτάμε τώρα τον αριθμητή

. Αφού τα

είναι πολυώνυμα, έχουμε


που από το Λήμμα είναι πολυώνυμο του

.
Όμοια και ο παρονομαστής

, και λοιπά.
 πολυώνυμο με πραγματικούς συντελεστές,
πολυώνυμο με πραγματικούς συντελεστές,  φυσικός αριθμός και
φυσικός αριθμός και  . Να αποδέιξετε ότι αν ισχύει η ταυτότητα
. Να αποδέιξετε ότι αν ισχύει η ταυτότητα  , τότε υπάρχει πολυώνυμο
, τότε υπάρχει πολυώνυμο  τέτοιο, ώστε
τέτοιο, ώστε  .
. είναι ρητή συνάρτηση αν μπορεί να γραφεί στην μορφή
είναι ρητή συνάρτηση αν μπορεί να γραφεί στην μορφή  , όπου
, όπου  πολυώνυμα με πραγματικούς συντελεστές. Να αποδείξετε ότι αν μια ρητή συνάρτηση
πολυώνυμα με πραγματικούς συντελεστές. Να αποδείξετε ότι αν μια ρητή συνάρτηση  ικανοποιεί την ταυτότητα
ικανοποιεί την ταυτότητα  , τότε υπάρχει ρητή συνάρτηση
, τότε υπάρχει ρητή συνάρτηση  τέτοια, ώστε
τέτοια, ώστε  .
.
 το
το  εκφράζεται ως πολυώνυμο του
εκφράζεται ως πολυώνυμο του  .
. έχουμε
έχουμε  , που είναι δευτεροβάθμιο πολυώνυμο του
, που είναι δευτεροβάθμιο πολυώνυμο του  έχουμε για το
έχουμε για το  ότι
ότι ,
,  τότε η υπόθεση
τότε η υπόθεση 
 , από όπου το ζητούμενο.
, από όπου το ζητούμενο.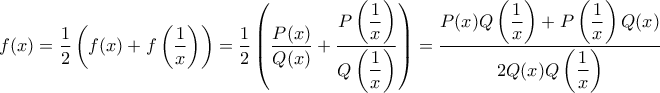
 . Αφού τα
. Αφού τα 

 .
. , και λοιπά.
, και λοιπά.