Οι μαθητές των θεωρητικών επιστημών πρέπει να λύσουν τα θέματα των ενοτήτων 1 και 2 (προβλήματα 1-20, σύνολο 160 μόρια, χρόνος 2 ώρες). Οι μαθητές των θετικών επιστημών πρέπει να λύσουν και τις τρεις ενότητες (προβλήματα 1-23, σύνολο 200 μόρια, χρόνος δυόμιση ώρες).
Ενότητα 1. Συμπληρώστε τα κενά (14 ερωτήσεις, 5 μόρια η καθεμία, σύνολο 70 μόρια).
1. Δίνονται τα σύνολα
 και
και  ,
,  .
.2. Δίνεται ο μιγαδικός αριθμός
 , όπου
, όπου  η μιγαδική μονάδα. Το πραγματικό μέρος του
η μιγαδική μονάδα. Το πραγματικό μέρος του  είναι
είναι  .
.3. Στο καρτεσιανό επίπεδο
 η απόσταση μεταξύ των εστιών της υπερβολής
η απόσταση μεταξύ των εστιών της υπερβολής  είναι
είναι  .
.4. Δεδομένου των δηγμάτων
 η τυπική απόκλιση ισούται με
η τυπική απόκλιση ισούται με  .
.5. Το πεδίο ορισμού της συνάρτησης
 είναι
είναι  .
.6. Δεδομένου του διαγράμματος ροής του παρακάτω αλγορίθμου, η έξοδος είναι ίση με
 .
.
7. Ρίχνουμε ένα αμερόληπτο ζάρι (κύβο με τους αριθμούς
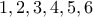 σε κάθε έδρα) δυο φορές. Η πιθανότητα του αθροίσματος των αριθμών της πάνω έδρας να είναι μικρότερο του
σε κάθε έδρα) δυο φορές. Η πιθανότητα του αθροίσματος των αριθμών της πάνω έδρας να είναι μικρότερο του  είναι
είναι  .
.8. Δίνεται η αριθμητική πρόοδος
 ,
,  είναι το άθροισμα των πρώτων
είναι το άθροισμα των πρώτων  όρων της. Αν
όρων της. Αν  ,
,  , τότε η τιμή του
, τότε η τιμή του  είναι
είναι  .
.9. Ο αριθμός των σημείων τομής των γραφικών παραστάσεων των συναρτήσεων
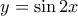 και
και  στο διάστημα
στο διάστημα ![[0, 3 \pi] [0, 3 \pi]](/forum/ext/geomar/texintegr/latexrender/pictures/ba62e9744d80b01cd47a8549721a4cab.png) είναι
είναι  .
.10. Στο παρακάτω σχήμα,
 είναι η δεξιά εστία της έλλειψης
είναι η δεξιά εστία της έλλειψης  ,
,  . Η ευθεία
. Η ευθεία  τέμνει την έλλειψη στα σημεία
τέμνει την έλλειψη στα σημεία  και
και  . Τότε η εκκεντρότητα της έλλειψης ισούται
. Τότε η εκκεντρότητα της έλλειψης ισούται  .
11. Έστω
.
11. Έστω  περιοδική συνάρτηση με πεδίο ορισμού το
περιοδική συνάρτηση με πεδίο ορισμού το  και περίοδο
και περίοδο  . Στο διάστημα
. Στο διάστημα 

Όπου
 . Αν
. Αν  , τότε
, τότε  ισούται
ισούται  .
.12. Οι πραγματικοί αριθμοί
 ικανοποιούν το σύστημα
ικανοποιούν το σύστημα
Τότε το εύρος τιμών της παράστασης
 είναι
είναι  .
.13. Στο παρακάτω τρίγωνο
 το σημείο
το σημείο  είναι το μέσο του τμήματος
είναι το μέσο του τμήματος  . Τα σημεία
. Τα σημεία  χωρίζουν το
χωρίζουν το  σε τρία ίσα μέρη.
σε τρία ίσα μέρη. 
 . Τότε
. Τότε  .
.
14. Αν σε ένα οξυγώνιο τρίγωνο
 ισχύει
ισχύει  , τότε η μέγιστη τιμή της παράστασης
, τότε η μέγιστη τιμή της παράστασης  είναι
είναι  .
.Έπεται δημοσίευση με τα θέματα της 2ης ενότητας...

 ,
,  .
. ;
;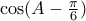 ;
; παρακάτω
παρακάτω  είναι τα μέσα των ακμών
είναι τα μέσα των ακμών  αντίστοιχα. Το σημείο
αντίστοιχα. Το σημείο  ,
,  ,
, 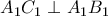 . Να αποδείξετε ότι:
. Να αποδείξετε ότι: παράλληλη στο επίπεδο
παράλληλη στο επίπεδο  .
. είναι κάθετο στο επίπεδο
είναι κάθετο στο επίπεδο  και το κάτω μέρος ένα τετραγωνικό ορθό πρίσμα
και το κάτω μέρος ένα τετραγωνικό ορθό πρίσμα  (όπως στο σχήμα παρακάτω). Το ύψος
(όπως στο σχήμα παρακάτω). Το ύψος  της ορθής τετραγωνικής πυραμίδας πρέπει να είναι τέσσερις φορές μεγαλύτερο από το ύψος
της ορθής τετραγωνικής πυραμίδας πρέπει να είναι τέσσερις φορές μεγαλύτερο από το ύψος  της τετραγωνικής πυραμίδας.
της τετραγωνικής πυραμίδας.  ,
,  πόσο είναι ο όγκος της αποθήκης;
πόσο είναι ο όγκος της αποθήκης; , ποιο είναι το μήκος του
, ποιο είναι το μήκος του  με κέντρο
με κέντρο 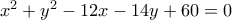 και
και  σημείο του
σημείο του  εφάπτεται του άξονα
εφάπτεται του άξονα  και εξωτερικά του κύκλου
και εξωτερικά του κύκλου  . Ποια η εξίσωση του κύκλου
. Ποια η εξίσωση του κύκλου  ευθεία παράλληλη στο
ευθεία παράλληλη στο  και τέμνει τον
και τέμνει τον 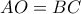 . Ποια είναι η εξίσωση της ευθείας
. Ποια είναι η εξίσωση της ευθείας  ικανοποιεί τις εξής συνθήκες: υπάρχουν σημεία
ικανοποιεί τις εξής συνθήκες: υπάρχουν σημεία  στον
στον  . Ποιο είναι το σύνολο τιμών των τιμών του
. Ποιο είναι το σύνολο τιμών των τιμών του  ;
;  (
( ).
).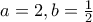 .
. .
.  ισχύει
ισχύει  . Ποια η μέγιστη δυνατή τιμή του
. Ποια η μέγιστη δυνατή τιμή του  ;
; και η συνάρτηση
και η συνάρτηση 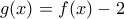 μηδενίζεται σε ένα μόνο σημείο, ποια η τιμή του γινομένου
μηδενίζεται σε ένα μόνο σημείο, ποια η τιμή του γινομένου  ;
; και
και  (
( ) μια ακολουθία. Έστω
) μια ακολουθία. Έστω  ένα υποσύνολο του
ένα υποσύνολο του  . Ορίζουμε
. Ορίζουμε  αν
αν  και
και  αν
αν  . Για παράδειγμα, αν
. Για παράδειγμα, αν  , τότε
, τότε  . Τώρα υποθέστε ότι η ακολουθία
. Τώρα υποθέστε ότι η ακολουθία  . Εξάλλου
. Εξάλλου  για
για  .
.  , αν
, αν  , τότε
, τότε  .
. ,
,  ,
,  . Να αποδείξετε ότι
. Να αποδείξετε ότι  .
. ,
,  .
.  είναι το μέσο της
είναι το μέσο της  .
.
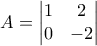 και ο αντίστροφος πίνακας του
και ο αντίστροφος πίνακας του  ,
,  . Πόσο ισούται το γινόμενο
. Πόσο ισούται το γινόμενο  , όπου
, όπου  είναι
είναι  , όπου
, όπου  παράμετρος. Έστω ότι η ευθεία
παράμετρος. Έστω ότι η ευθεία  . Πόσο είναι το μήκος του τμήματος
. Πόσο είναι το μήκος του τμήματος  ;
; ,
,  ,
,  . Αποδείξτε ότι
. Αποδείξτε ότι  .
. και η παραβολή
και η παραβολή  , όπως φαίνεται στο παρακάτω σχήμα.
, όπως φαίνεται στο παρακάτω σχήμα. είναι
είναι  .
. ;
;
 ;
; ,
,  . Να αποδείξετε, ότι
. Να αποδείξετε, ότι .
. πρέπει να γίνει
πρέπει να γίνει 
 , τότε
, τότε  , άρα το πραγματικό μέρος του
, άρα το πραγματικό μέρος του  .
.
 και
και 
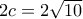 , διότι:
, διότι:  και
και  .
.
![x\in [-3,1] x\in [-3,1]](/forum/ext/geomar/texintegr/latexrender/pictures/080a02c901660db0a1f603fe48bc33b9.png)

 , συνολικά 6 περιπτώσεις.
, συνολικά 6 περιπτώσεις. οπότε η ζητούμενη πιθανότητα είναι:
οπότε η ζητούμενη πιθανότητα είναι:

 οπότε:
οπότε: 
 στο
στο 

 και σχεδιάζοντας τα χωρία, προκύπτει το παρακάτω σχήμα:
και σχεδιάζοντας τα χωρία, προκύπτει το παρακάτω σχήμα: δηλαδή, από τη λύση του συστήματός τους:
δηλαδή, από τη λύση του συστήματός τους:

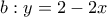 οπότε, το ελάχιστο της
οπότε, το ελάχιστο της  δηλαδή:
δηλαδή: 

![\left [ \dfrac{4}{5},16 \right ] \left [ \dfrac{4}{5},16 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/997228693927a500c13a181a272232af.png)
 και
και 
 , οπότε:
, οπότε: 
 :
: 



 . Η ευθεία
. Η ευθεία  έχω
έχω  άρα
άρα  άρα
άρα 

 έχουμε
έχουμε  οπότε
οπότε 
 και
και 
 .
. . Τότε
. Τότε 

 .
.
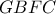 παραλληλόγραμμό, βλέπε σχήμα).
παραλληλόγραμμό, βλέπε σχήμα). 


 μέσο του
μέσο του  ).
).
 .
. . Ποιο είναι το σύνολο τιμών των τιμών του t;
. Ποιο είναι το σύνολο τιμών των τιμών του t;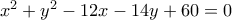 έχω με συμπλήρωση τετραγώνου την εξίσωση
έχω με συμπλήρωση τετραγώνου την εξίσωση  , άρα
, άρα 
 και ακτίνα
και ακτίνα  άρα
άρα  άρα
άρα 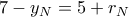
 και τελικά
και τελικά 

 άρα
άρα 

 κάθετο στη χορδή
κάθετο στη χορδή  έχουμε:
έχουμε:



 ή
ή 









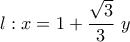




 ή
ή 
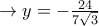
 . Έχουμε ακόμα
. Έχουμε ακόμα 



 ή χάνω κάτι;
ή χάνω κάτι; ανήκει στην ευθεία
ανήκει στην ευθεία  ή
ή 
 οπότε το μέσο του
οπότε το μέσο του 






 .
. 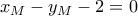 άρα
άρα 

 και ανάμεσα στους δυο κλάδους της παραβολής.
και ανάμεσα στους δυο κλάδους της παραβολής. και
και 
 και
και 
 και
και  ή
ή  ή
ή  ή
ή  ή
ή  .
.