
Λύσεις τράπεζας θεμάτων άλγεβρας σε latex
Συντονιστής: stranton
-
dimitra_gi
- Δημοσιεύσεις: 3
- Εγγραφή: Κυρ Σεπ 11, 2011 7:18 pm
Re: Λύσεις τράπεζας θεμάτων άλγεβρας σε latex
Καταρχήν το μηδέν είναι ακέραιος οπότε το θεωρούμε κι αυτό υποψήφιο για ρίζα. Θα το κοιτάξω να σου πω για τα περαιτέρω πώς λύνεται.
-
dimitra_gi
- Δημοσιεύσεις: 3
- Εγγραφή: Κυρ Σεπ 11, 2011 7:18 pm
Re: Λύσεις τράπεζας θεμάτων άλγεβρας σε latex
Επειδή ζητείται το τριώνυμο να έχει θετική τιμή για κάθε χ μικρότερο ή ισο του μηδενός ,για αυτό ρώτησα αν μπορεί να θεωρηθεί λύση το μηδέν.Αλλιώς η μοναδική περίπτωση είναι οι λύσεις 1,2. Και η επόμενη ερώτηση μου αφορούσε την περίπτωση να είναι διπλή η λύση 1 ή διπλή η λύση 2; Δεν είναι σαφές από την εκφώνηση αν οι λύσεις πρέπει να είναι άνισες ή υπάρχει και η περίπτωση να είναι ίσες.
Re: Λύσεις τράπεζας θεμάτων άλγεβρας σε latex
Είναι σωστές οι σκέψεις σου, αλλα επειδή δε το ξεκαθαρίζει ας θεωρήσουμε ολες τις περιπτώσεις και βλέπουμε. Μάλλον εννοεί να είναι διακριτές αλλα ας δούμε και την περίπτωση να ναι διπλή.
Re: Λύσεις τράπεζας θεμάτων άλγεβρας σε latex
Καλησπέρα. Είναι από το ζόρικα τέταρτα θέματα, αφού ο μαθητής πρέπει να έχει κατανοήσει πολύ καλά τα περί προσήμου τριωνύμου για να κάνει σωστά τη διερεύνηση.dimitra_gi έγραψε:Στο τέταρτο θέμα 7677 στο γ) υποερώτημα το μηδέν μπορεί να θεωρηθεί ως η μία λύση από τις 2 που ψάχνουμε ή η μοναδική περίπτωση είναι οι λύσεις 1 και 2;Επίσης μπορεί και σαν περίπτωση να υπάρχει διπλή λύση η 1 ή διπλή λύση η 2;
Για τις ερωτήσεις της Δήμητρας:
οι ρίζες είναι αναγκαστικά
 και
και  . Το
. Το  δεν μπορεί να είναι ρίζα, αφού τότε το τριώνυμο δεν θα ήταν θετικό στο
δεν μπορεί να είναι ρίζα, αφού τότε το τριώνυμο δεν θα ήταν θετικό στο  , όπως απαιτεί η εκφώνηση, αλλά θα μηδενιζόταν. Επίσης δεν μπορεί να έχω διπλή λύση, αφού και πάλι από εκφώνηση το τριώνυμο θέλουμε να έχει ρίζες δύο από τις ακέραιες λύσεις.
, όπως απαιτεί η εκφώνηση, αλλά θα μηδενιζόταν. Επίσης δεν μπορεί να έχω διπλή λύση, αφού και πάλι από εκφώνηση το τριώνυμο θέλουμε να έχει ρίζες δύο από τις ακέραιες λύσεις.Re: Λύσεις τράπεζας θεμάτων άλγεβρας σε latex
Άσκηση 4_7677
Λύση
α)
β) Προφανώς οι ακέραιες λύσεις είναι το σύνολο
γ) το τριώνυμο είναι θετικό για κάθε
είναι θετικό για κάθε  και άρα
και άρα  .
.
Αλλά από τους τύπους του Vieta για τις ρίζες του τριωνύμου είναι για το δεδομένο τριώνυμο
είναι για το δεδομένο τριώνυμο  συνεπώς οι ρίζες που θα επιλέξουμε από το
συνεπώς οι ρίζες που θα επιλέξουμε από το  θα πρέπει να είναι ομόσημες
θα πρέπει να είναι ομόσημες
( αυτόματα αποκλείεται η τιμή ).
).
Δεν γίνεται να είναι οι ρίζες ίσες και αρνητικές γιατί τότε το τριώνυμο θα γίνεται μηδέν όταν η τιμή του συμπέσει με την ρίζα αυτή.
συμπέσει με την ρίζα αυτή.
Εξετάζουμε τώρα αν γίνεται να είναι ρίζες δύο διακεκριμένες αρνητικές τιμές του .
.
Σε τέτοια περίπτωση, ισχύει ότι και προηγουμένως δηλαδή το τριώνυμο θα μηδενίζεται όταν η τιμή του συμπέσει με μια από τις ρίζες ( Σωστή παρέμβαση του Κ. Κυριαζή)
συμπέσει με μια από τις ρίζες ( Σωστή παρέμβαση του Κ. Κυριαζή)
(Επί πλέον δε οι τιμές του τριωνύμου ανάμεσα στις ρίζες αυτές θα είναι ετερόσημες του που πάλι έρχεται σε αντίφαση με τις προϋποθέσεις της άσκησης).
που πάλι έρχεται σε αντίφαση με τις προϋποθέσεις της άσκησης).
Μετά από τα παραπάνω το τριώνυμο θα έχει για ρίζες είτε τις δύο διακεκριμένες θετικές τιμές του συνόλου , δηλαδή τις
, δηλαδή τις  και
και 
είτε διπλή κάθε μια απ’ αυτές και πράγματι τότε ή
ή  που είναι θετικό για κάθε
που είναι θετικό για κάθε  .
.
Αυτό το τελευταίο με τις διπλές ρίζες που γράφω ελέγχετε. Όμως ο θεματοδότης έπρεπε ρητά να αποκλείει τέτοιο ενδεχόμενο με τη φράση διακεκριμένες
Νίκος
Λύση
α)

β) Προφανώς οι ακέραιες λύσεις είναι το σύνολο

γ) το τριώνυμο
 είναι θετικό για κάθε
είναι θετικό για κάθε  και άρα
και άρα  .
.Αλλά από τους τύπους του Vieta για τις ρίζες του τριωνύμου
 είναι για το δεδομένο τριώνυμο
είναι για το δεδομένο τριώνυμο  συνεπώς οι ρίζες που θα επιλέξουμε από το
συνεπώς οι ρίζες που θα επιλέξουμε από το  θα πρέπει να είναι ομόσημες
θα πρέπει να είναι ομόσημες ( αυτόματα αποκλείεται η τιμή
 ).
). Δεν γίνεται να είναι οι ρίζες ίσες και αρνητικές γιατί τότε το τριώνυμο θα γίνεται μηδέν όταν η τιμή του
 συμπέσει με την ρίζα αυτή.
συμπέσει με την ρίζα αυτή.Εξετάζουμε τώρα αν γίνεται να είναι ρίζες δύο διακεκριμένες αρνητικές τιμές του
 .
.Σε τέτοια περίπτωση, ισχύει ότι και προηγουμένως δηλαδή το τριώνυμο θα μηδενίζεται όταν η τιμή του
 συμπέσει με μια από τις ρίζες ( Σωστή παρέμβαση του Κ. Κυριαζή)
συμπέσει με μια από τις ρίζες ( Σωστή παρέμβαση του Κ. Κυριαζή)(Επί πλέον δε οι τιμές του τριωνύμου ανάμεσα στις ρίζες αυτές θα είναι ετερόσημες του
 που πάλι έρχεται σε αντίφαση με τις προϋποθέσεις της άσκησης).
που πάλι έρχεται σε αντίφαση με τις προϋποθέσεις της άσκησης).Μετά από τα παραπάνω το τριώνυμο θα έχει για ρίζες είτε τις δύο διακεκριμένες θετικές τιμές του συνόλου
 , δηλαδή τις
, δηλαδή τις  και
και 
είτε διπλή κάθε μια απ’ αυτές και πράγματι τότε
 ή
ή  που είναι θετικό για κάθε
που είναι θετικό για κάθε  .
.Αυτό το τελευταίο με τις διπλές ρίζες που γράφω ελέγχετε. Όμως ο θεματοδότης έπρεπε ρητά να αποκλείει τέτοιο ενδεχόμενο με τη φράση διακεκριμένες
Νίκος
τελευταία επεξεργασία από Doloros σε Δευ Ιουν 09, 2014 12:50 am, έχει επεξεργασθεί 1 φορά συνολικά.
- exdx
- Επιμελητής
- Δημοσιεύσεις: 1742
- Εγγραφή: Κυρ Δεκ 21, 2008 6:00 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: Λύσεις τράπεζας θεμάτων άλγεβρας σε latex
GI_A_ALG_4_1868
Σε ένα τμήμα της Α’ Λυκείου κάποιοι μαθητές παρακολουθούν μαθήματα Αγγλικών και κάποιοι Γαλλικών.
Η πιθανότητα ένας μαθητής να μην παρακολουθεί Γαλλικά είναι .
.
Η πιθανότητα ένας μαθητής να παρακολουθεί Αγγλικά είναι τετραπλάσια από την πιθανότητα να παρακολουθεί Γαλλικά.
Τέλος, η πιθανότητα ένας μαθητής να παρακολουθεί μαθήματα τουλάχιστον μιας από τις δύο γλώσσες είναι .
.
α) Επιλέγουμε ένα μαθητή στην τύχη.
i) Ποια είναι η πιθανότητα αυτός να παρακολουθεί μαθήματα και των δύο γλωσσών;
ii) Ποια είναι η πιθανότητα αυτός να παρακολουθεί μαθήματα μόνο μιας από τις δύο γλώσσες;
β) Αν μαθητές παρακολουθούν μόνο Αγγλικά, πόσοι είναι οι μαθητές του τμήματος ;
μαθητές παρακολουθούν μόνο Αγγλικά, πόσοι είναι οι μαθητές του τμήματος ;
Λύση
α) Ορίζουμε τα ενδεχόμενα :
 : Ο μαθητής παρακολουθεί Αγγλικά ,
: Ο μαθητής παρακολουθεί Αγγλικά ,  : Ο μαθητής παρακολουθεί Γαλλικά ,
: Ο μαθητής παρακολουθεί Γαλλικά ,
οπότε το ενδεχόμενο : είναι ο μαθητής να παρακολουθεί μαθήματα τουλάχιστον μιας από τις δύο γλώσσες .
είναι ο μαθητής να παρακολουθεί μαθήματα τουλάχιστον μιας από τις δύο γλώσσες .
Δίνεται ότι
 και
και 
Ακόμα
ι ) Ζητούμε την πιθανότητα

ιι) Ζητούμε την πιθανότητα![\displaystyle{{\rm P}\left[ {({\rm A} - \Gamma ) \cup (\Gamma - {\rm A})} \right]} \displaystyle{{\rm P}\left[ {({\rm A} - \Gamma ) \cup (\Gamma - {\rm A})} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/2e57219209b75de9924c3f385d834cbb.png) και επειδή τα ενδεχόμενα
και επειδή τα ενδεχόμενα  είναι ασυμβίβαστα , έχουμε :
είναι ασυμβίβαστα , έχουμε :
![\displaystyle{\begin{array}{l}
{\rm P}\left[ {({\rm A} - \Gamma ) \cup (\Gamma - {\rm A})} \right] = {\rm P}(\Gamma - {\rm A}) + {\rm P}({\rm A} - \Gamma ) = {\rm P}(\Gamma ) - {\rm P}({\rm A} \cap \Gamma ) + {\rm P}({\rm A}) - {\rm P}({\rm A} \cap \Gamma ) = \\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 0,2 + 0,8 - 2 \cdot 0,1 = 0,8 \\
\end{array}} \displaystyle{\begin{array}{l}
{\rm P}\left[ {({\rm A} - \Gamma ) \cup (\Gamma - {\rm A})} \right] = {\rm P}(\Gamma - {\rm A}) + {\rm P}({\rm A} - \Gamma ) = {\rm P}(\Gamma ) - {\rm P}({\rm A} \cap \Gamma ) + {\rm P}({\rm A}) - {\rm P}({\rm A} \cap \Gamma ) = \\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 0,2 + 0,8 - 2 \cdot 0,1 = 0,8 \\
\end{array}}](/forum/ext/geomar/texintegr/latexrender/pictures/540697dd47ae7bac511a13d679863727.png)
β) Είναι :
και
Σε ένα τμήμα της Α’ Λυκείου κάποιοι μαθητές παρακολουθούν μαθήματα Αγγλικών και κάποιοι Γαλλικών.
Η πιθανότητα ένας μαθητής να μην παρακολουθεί Γαλλικά είναι
 .
. Η πιθανότητα ένας μαθητής να παρακολουθεί Αγγλικά είναι τετραπλάσια από την πιθανότητα να παρακολουθεί Γαλλικά.
Τέλος, η πιθανότητα ένας μαθητής να παρακολουθεί μαθήματα τουλάχιστον μιας από τις δύο γλώσσες είναι
 .
.α) Επιλέγουμε ένα μαθητή στην τύχη.
i) Ποια είναι η πιθανότητα αυτός να παρακολουθεί μαθήματα και των δύο γλωσσών;
ii) Ποια είναι η πιθανότητα αυτός να παρακολουθεί μαθήματα μόνο μιας από τις δύο γλώσσες;
β) Αν
 μαθητές παρακολουθούν μόνο Αγγλικά, πόσοι είναι οι μαθητές του τμήματος ;
μαθητές παρακολουθούν μόνο Αγγλικά, πόσοι είναι οι μαθητές του τμήματος ;Λύση
α) Ορίζουμε τα ενδεχόμενα :
 : Ο μαθητής παρακολουθεί Αγγλικά ,
: Ο μαθητής παρακολουθεί Αγγλικά ,  : Ο μαθητής παρακολουθεί Γαλλικά ,
: Ο μαθητής παρακολουθεί Γαλλικά , οπότε το ενδεχόμενο :
 είναι ο μαθητής να παρακολουθεί μαθήματα τουλάχιστον μιας από τις δύο γλώσσες .
είναι ο μαθητής να παρακολουθεί μαθήματα τουλάχιστον μιας από τις δύο γλώσσες .Δίνεται ότι
 και
και 
Ακόμα

ι ) Ζητούμε την πιθανότητα

ιι) Ζητούμε την πιθανότητα
![\displaystyle{{\rm P}\left[ {({\rm A} - \Gamma ) \cup (\Gamma - {\rm A})} \right]} \displaystyle{{\rm P}\left[ {({\rm A} - \Gamma ) \cup (\Gamma - {\rm A})} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/2e57219209b75de9924c3f385d834cbb.png) και επειδή τα ενδεχόμενα
και επειδή τα ενδεχόμενα  είναι ασυμβίβαστα , έχουμε :
είναι ασυμβίβαστα , έχουμε :![\displaystyle{\begin{array}{l}
{\rm P}\left[ {({\rm A} - \Gamma ) \cup (\Gamma - {\rm A})} \right] = {\rm P}(\Gamma - {\rm A}) + {\rm P}({\rm A} - \Gamma ) = {\rm P}(\Gamma ) - {\rm P}({\rm A} \cap \Gamma ) + {\rm P}({\rm A}) - {\rm P}({\rm A} \cap \Gamma ) = \\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 0,2 + 0,8 - 2 \cdot 0,1 = 0,8 \\
\end{array}} \displaystyle{\begin{array}{l}
{\rm P}\left[ {({\rm A} - \Gamma ) \cup (\Gamma - {\rm A})} \right] = {\rm P}(\Gamma - {\rm A}) + {\rm P}({\rm A} - \Gamma ) = {\rm P}(\Gamma ) - {\rm P}({\rm A} \cap \Gamma ) + {\rm P}({\rm A}) - {\rm P}({\rm A} \cap \Gamma ) = \\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 0,2 + 0,8 - 2 \cdot 0,1 = 0,8 \\
\end{array}}](/forum/ext/geomar/texintegr/latexrender/pictures/540697dd47ae7bac511a13d679863727.png)
β) Είναι :

και

Kαλαθάκης Γιώργης
- exdx
- Επιμελητής
- Δημοσιεύσεις: 1742
- Εγγραφή: Κυρ Δεκ 21, 2008 6:00 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: Λύσεις τράπεζας θεμάτων άλγεβρας σε latex
GI_A_ALG_4_1874
Δίνεται η εξίσωση: , με παράμετρο
, με παράμετρο  .
.
α) Να δείξετε ότι η διακρίνουσα της εξίσωσης είναι:
είναι: 
β) Να βρείτε τις τιμές του , ώστε η εξίσωση να έχει δύο ρίζες πραγματικές και άνισες.
, ώστε η εξίσωση να έχει δύο ρίζες πραγματικές και άνισες.
γ) Αν η εξίσωση έχει ρίζες τους αριθμούς και
και  είναι η απόσταση των
είναι η απόσταση των  στον άξονα των πραγματικών αριθμών, να βρείτε για ποιες τιμές του ισχύει:
στον άξονα των πραγματικών αριθμών, να βρείτε για ποιες τιμές του ισχύει: 
Λύση
α) Είναι :
β) Η εξίσωση θα έχει δύο ρίζες πραγματικές και άνισες αν και μόνο αν :
 .
.
Το τριώνυμο έχει :
έχει :  , ρίζες τις
, ρίζες τις  και
και 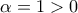 .
.
Επομένως :
γ) Εφόσον η εξίσωση έχει δυο ρίζες , έχουμε ότι : ή
ή  . Τότε :
. Τότε :

Από τους τύπους Vieta και από την έχουμε ότι :
έχουμε ότι :
 , οπότε η
, οπότε η  γίνεται :
γίνεται :

Οι ρίζες αυτές είναι και οι δύο δεκτές .
Εdit : Μετά την παρέμβαση του Stopjohn (παρακάτω στην ίδια σελίδα ) και μόνο για να καλύψω την παράλειψη του θεματοδότη συμπληρώνω το (γ) ερώτημα :
Στην περίπτωση που οι ρίζες είναι ίσες τότε άτοπο.
άτοπο.
Επίσης
Επομένως οι τιμές που βρέθηκαν στο (γ) ερώτημα εξακολουθούν να είναι δεκτές .
ΥΓ : Όπως λέει κι ο Γιάννης παρακάτω , δεν απαιτούμε τέτοια διερεύνηση από τους μαθητές
Δίνεται η εξίσωση:
 , με παράμετρο
, με παράμετρο  .
.α) Να δείξετε ότι η διακρίνουσα της εξίσωσης
 είναι:
είναι: 
β) Να βρείτε τις τιμές του
 , ώστε η εξίσωση να έχει δύο ρίζες πραγματικές και άνισες.
, ώστε η εξίσωση να έχει δύο ρίζες πραγματικές και άνισες.γ) Αν η εξίσωση έχει ρίζες τους αριθμούς
 και
και  είναι η απόσταση των
είναι η απόσταση των  στον άξονα των πραγματικών αριθμών, να βρείτε για ποιες τιμές του ισχύει:
στον άξονα των πραγματικών αριθμών, να βρείτε για ποιες τιμές του ισχύει: 
Λύση
α) Είναι :

β) Η εξίσωση θα έχει δύο ρίζες πραγματικές και άνισες αν και μόνο αν :
 .
.Το τριώνυμο
 έχει :
έχει :  , ρίζες τις
, ρίζες τις  και
και 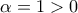 .
. Επομένως :

γ) Εφόσον η εξίσωση έχει δυο ρίζες , έχουμε ότι :
 ή
ή  . Τότε :
. Τότε :
Από τους τύπους Vieta και από την
 έχουμε ότι :
έχουμε ότι :  , οπότε η
, οπότε η  γίνεται :
γίνεται :
Οι ρίζες αυτές είναι και οι δύο δεκτές .
Εdit : Μετά την παρέμβαση του Stopjohn (παρακάτω στην ίδια σελίδα ) και μόνο για να καλύψω την παράλειψη του θεματοδότη συμπληρώνω το (γ) ερώτημα :
Στην περίπτωση που οι ρίζες είναι ίσες τότε
 άτοπο.
άτοπο.Επίσης

Επομένως οι τιμές που βρέθηκαν στο (γ) ερώτημα εξακολουθούν να είναι δεκτές .
ΥΓ : Όπως λέει κι ο Γιάννης παρακάτω , δεν απαιτούμε τέτοια διερεύνηση από τους μαθητές
τελευταία επεξεργασία από exdx σε Τετ Ιουν 11, 2014 9:17 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Kαλαθάκης Γιώργης
- exdx
- Επιμελητής
- Δημοσιεύσεις: 1742
- Εγγραφή: Κυρ Δεκ 21, 2008 6:00 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: Λύσεις τράπεζας θεμάτων άλγεβρας σε latex
GI_A_ALG_4_1880
Δίνεται η συνάρτηση , με
, με 
α) Να βρείτε το πεδίο ορισμού της συνάρτησης .
.
β) Να βρείτε τα σημεία τομής της γραφικής παράστασης της συνάρτησης με τους άξονες.
γ) Αν είναι τα σημεία τομής της γραφικής παράστασης της συνάρτησης με τους άξονες αντίστοιχα,
αντίστοιχα,
να βρείτε την εξίσωση της ευθείας που ορίζεται από τα
Λύση
α) Η ορίζεται αν και μόνο αν :
ορίζεται αν και μόνο αν :  ,
,
επομένως είναι :
β) Για , είναι
, είναι  , επομένως τέμνει τον
, επομένως τέμνει τον  στο
στο 
Για , είναι
, είναι  , επομένως τέμνει τον
, επομένως τέμνει τον  στο
στο 
γ) Έστω η εξίσωση της ευθείας (ε) . Τα σημεία
η εξίσωση της ευθείας (ε) . Τα σημεία  , ανήκουν στην ευθεία , οπότε αντικαθιστώντας τις συντεταγμένες τους σχηματίζουμε το σύστημα :
, ανήκουν στην ευθεία , οπότε αντικαθιστώντας τις συντεταγμένες τους σχηματίζουμε το σύστημα :

Επομένως είναι η
Δίνεται η συνάρτηση
 , με
, με 
α) Να βρείτε το πεδίο ορισμού της συνάρτησης
 .
. β) Να βρείτε τα σημεία τομής της γραφικής παράστασης της συνάρτησης με τους άξονες.
γ) Αν είναι τα σημεία τομής της γραφικής παράστασης της συνάρτησης με τους άξονες
 αντίστοιχα,
αντίστοιχα, να βρείτε την εξίσωση της ευθείας που ορίζεται από τα

Λύση
α) Η
 ορίζεται αν και μόνο αν :
ορίζεται αν και μόνο αν :  ,
,επομένως είναι :

β) Για
 , είναι
, είναι  , επομένως τέμνει τον
, επομένως τέμνει τον  στο
στο 
Για
 , είναι
, είναι  , επομένως τέμνει τον
, επομένως τέμνει τον  στο
στο 
γ) Έστω
 η εξίσωση της ευθείας (ε) . Τα σημεία
η εξίσωση της ευθείας (ε) . Τα σημεία  , ανήκουν στην ευθεία , οπότε αντικαθιστώντας τις συντεταγμένες τους σχηματίζουμε το σύστημα :
, ανήκουν στην ευθεία , οπότε αντικαθιστώντας τις συντεταγμένες τους σχηματίζουμε το σύστημα :
Επομένως είναι η

Kαλαθάκης Γιώργης
Re: Λύσεις τράπεζας θεμάτων άλγεβρας σε latex
Άσκηση 4542
α) Να λύσετε την ανίσωση: στο σύνολο των πραγματικών αριθμών.
στο σύνολο των πραγματικών αριθμών.
(Μονάδες 8)
β) Δίνεται ένας πραγματικός αριθμός με
με 
i) Να βάλετε στη σειρά, από τον μικρότερο στον μεγαλύτερο και να τοποθετήσετε
πάνω στον άξονα των πραγματικών αριθμών, τους αριθμούς:
 Να αιτιολογήσετε την απάντησή σας με τη βοήθεια και του ερωτήματος α). (Mονάδες 10)
Να αιτιολογήσετε την απάντησή σας με τη βοήθεια και του ερωτήματος α). (Mονάδες 10)
ii) Να αποδείξετε ότι ισχύει η ανισότητα: (Mονάδες 7)
(Mονάδες 7)
Λύση
α) (1)
(1)
θα βρούμε τις ρίζες της εξίσωσης
Όταν έχουμε ανίσωση 2ου βαθμού κάνουμε το πινακάκι: Άρα η (1) .
.
β) i. Από το α) αφού
Σύμφωνα με εφαρμογή του βιβλίου
 ( και αφού
( και αφού  )
) 
Επίσης
Επομένως
ii. Αφού θετικοί αριθμοί
θετικοί αριθμοί



 που ισχύει για κάθε
που ισχύει για κάθε  .
.
Άσκηση 4545
Δίνεται η συνάρτηση
α) Να βρείτε το πεδίο ορισμού Α της συνάρτησης . (Μονάδες 6)
. (Μονάδες 6)
β) Να αποδείξετε ότι για κάθε ισχύει:
ισχύει:  (Μονάδες 9)
(Μονάδες 9)
γ) Για , να λύσετε την εξίσωση:
, να λύσετε την εξίσωση: 
(Μονάδες 10)
Λύση
α) Θα πρέπει
Αρα το πεδίο ορισμού
β)
Αν στον αριθμητή θέσουμε τότε προκύπτει το τριώνυμο
τότε προκύπτει το τριώνυμο 
με και ρίζες που δίνονται από τον τύπο
και ρίζες που δίνονται από τον τύπο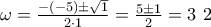
Άρα
Επομένως
Η εξίσωση με την βοήθεια της σχέσης
με την βοήθεια της σχέσης  γράφεται
γράφεται 

Αν θέσουμε τότε προκύπτει η εξίσωση
τότε προκύπτει η εξίσωση 
με και ρίζες που δίνονται από τον τύπο
και ρίζες που δίνονται από τον τύπο
Επομένως ( που απορρίπτεται λόγω του πεδίου ορισμού της
( που απορρίπτεται λόγω του πεδίου ορισμού της  )
)
ή που αποτελούν τις ρίζες της εξίσωσης.
που αποτελούν τις ρίζες της εξίσωσης.
α) Να λύσετε την ανίσωση:
 στο σύνολο των πραγματικών αριθμών.
στο σύνολο των πραγματικών αριθμών. (Μονάδες 8)
β) Δίνεται ένας πραγματικός αριθμός
 με
με 
i) Να βάλετε στη σειρά, από τον μικρότερο στον μεγαλύτερο και να τοποθετήσετε
πάνω στον άξονα των πραγματικών αριθμών, τους αριθμούς:
 Να αιτιολογήσετε την απάντησή σας με τη βοήθεια και του ερωτήματος α). (Mονάδες 10)
Να αιτιολογήσετε την απάντησή σας με τη βοήθεια και του ερωτήματος α). (Mονάδες 10)ii) Να αποδείξετε ότι ισχύει η ανισότητα:
 (Mονάδες 7)
(Mονάδες 7)Λύση
α)
 (1)
(1)θα βρούμε τις ρίζες της εξίσωσης

Όταν έχουμε ανίσωση 2ου βαθμού κάνουμε το πινακάκι: Άρα η (1)
 .
.β) i. Από το α) αφού

Σύμφωνα με εφαρμογή του βιβλίου
 ( και αφού
( και αφού  )
) 
Επίσης

Επομένως

ii. Αφού
 θετικοί αριθμοί
θετικοί αριθμοί


 που ισχύει για κάθε
που ισχύει για κάθε  .
.Άσκηση 4545
Δίνεται η συνάρτηση

α) Να βρείτε το πεδίο ορισμού Α της συνάρτησης
 . (Μονάδες 6)
. (Μονάδες 6)β) Να αποδείξετε ότι για κάθε
 ισχύει:
ισχύει:  (Μονάδες 9)
(Μονάδες 9)γ) Για
 , να λύσετε την εξίσωση:
, να λύσετε την εξίσωση: 
(Μονάδες 10)
Λύση
α) Θα πρέπει

Αρα το πεδίο ορισμού

β)

Αν στον αριθμητή θέσουμε
 τότε προκύπτει το τριώνυμο
τότε προκύπτει το τριώνυμο 
με
 και ρίζες που δίνονται από τον τύπο
και ρίζες που δίνονται από τον τύπο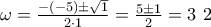
Άρα

Επομένως

Η εξίσωση
 με την βοήθεια της σχέσης
με την βοήθεια της σχέσης  γράφεται
γράφεται 

Αν θέσουμε
 τότε προκύπτει η εξίσωση
τότε προκύπτει η εξίσωση 
με
 και ρίζες που δίνονται από τον τύπο
και ρίζες που δίνονται από τον τύπο
Επομένως
 ( που απορρίπτεται λόγω του πεδίου ορισμού της
( που απορρίπτεται λόγω του πεδίου ορισμού της  )
)ή
 που αποτελούν τις ρίζες της εξίσωσης.
που αποτελούν τις ρίζες της εξίσωσης.- Συνημμένα
-
- 4542-4545.doc
- (161.5 KiB) Μεταφορτώθηκε 153 φορές
ΠΑΠΑΣΤΑΘΟΠΟΥΛΟΣ ΘΑΝΑΣΗΣ
Re: Λύσεις τράπεζας θεμάτων άλγεβρας σε latex
Άσκηση491
Δίνονται οι ανισώσεις: και
και
α) Να βρείτε τις λύσεις τους. (Μονάδες 15)
β) Να βρείτε το σύνολο των κοινών τους λύσεων. (Μονάδες 10)
Λύση
α) •
•

β) Άρα οι κοινές τους λύσεις είναι ή
ή  .
.
Άσκηση 492
Δίνεται η συνάρτηση .
.
α) Να υπολογίσετε το άθροισμα . (Μονάδες 10)
. (Μονάδες 10)
β) Να βρείτε τα κοινά σημεία της γραφικής της παράστασης της με τους άξονες.
με τους άξονες.
(Μονάδες 15)
Λύση
α)![\displaystyle{f\text{ }\left( -1 \right)+f\left( 0 \right)+f\left( 1 \right)=\left[ {{\left( -1 \right)}^{2}}+2\left( -1 \right)-15 \right]+\left[ {{0}^{2}}+2\cdot 0-15
\right]+\left[ {{1}^{2}}+2\cdot 1-15 \right]}
=\left \displaystyle{f\text{ }\left( -1 \right)+f\left( 0 \right)+f\left( 1 \right)=\left[ {{\left( -1 \right)}^{2}}+2\left( -1 \right)-15 \right]+\left[ {{0}^{2}}+2\cdot 0-15
\right]+\left[ {{1}^{2}}+2\cdot 1-15 \right]}
=\left](/forum/ext/geomar/texintegr/latexrender/pictures/571cee57c5ef5b830dd491a8855a1a4e.png)
![\left[ 1+2\left( -1 \right)-15 \right]+\left( -15 \right)+\left[ 1+2\cdot 1-15 \right]\
=\left( 1-2-15 \right)-15+\left( 1+2-15 \right)= \left[ 1+2\left( -1 \right)-15 \right]+\left( -15 \right)+\left[ 1+2\cdot 1-15 \right]\
=\left( 1-2-15 \right)-15+\left( 1+2-15 \right)=](/forum/ext/geomar/texintegr/latexrender/pictures/cdbfc6471ffc9231cb76db2afc055d1d.png)

Για να βρούμε τα κοινά σημεία της γραφικής της παράστασης της με τον άξονα
με τον άξονα βάζουμε όπου
βάζουμε όπου  .
.

Επομένως το κοινό σημείο είναι το
Για να βρούμε τα κοινά σημεία της γραφικής της παράστασης της με τον άξονα
με τον άξονα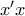 βάζουμε όπου
βάζουμε όπου  δηλαδή:
δηλαδή:

αφού
και οι ρίζες ,
,
Επμένως τα κοινά σημεία είναι τα και
και 
Άσκηση 493
α) Να λύσετε την εξίσωση . (Μονάδες 10)
. (Μονάδες 10)
β) Να σχηματίσετε εξίσωση δευτέρου βαθμού με ρίζες, τις ρίζες της εξίσωσης του α)
ερωτήματος. (Μονάδες 15)
Λύση
α)
β) Για να βρούμε μια δευτεροβάβμια αεξίσωση ενώ ξέρουμε τις ρίζες της χρησιμοποιούμε τον τύπο
όπου
και
Άρα .
.
Άσκηση 494
Οι διαστάσεις (σε m) του πατώματος του εργαστήριου της πληροφορικής ενός
σχολείου είναι και
και  , με
, με  .
.
α) Να γράψετε με τη βοήθεια του την περίμετρο και το εμβαδόν του πατώματος. (Μονάδες 10)
την περίμετρο και το εμβαδόν του πατώματος. (Μονάδες 10)
β) Αν το εμβαδόν του πατώματος του εργαστηρίου είναι , να βρείτε τις
, να βρείτε τις
διαστάσεις του. (Μονάδες 15)
Λύση
Προφανώς το πάτωμα του εργαστηρίου είναι Ορθογώνιο Παραλληλόγραμμο.
α) Η περίμετρος
Το Εμβαδόν: Ε
β) Ε ή
ή 
αφού και ρίζες
και ρίζες  ,
,
Όμως άρα
άρα  . Επομένως διαστάσεις του πατώματος του εργαστηρίου είναι
. Επομένως διαστάσεις του πατώματος του εργαστηρίου είναι  και
και .
.
Δίνονται οι ανισώσεις:
 και
και
α) Να βρείτε τις λύσεις τους. (Μονάδες 15)
β) Να βρείτε το σύνολο των κοινών τους λύσεων. (Μονάδες 10)
Λύση
α) •

•


β) Άρα οι κοινές τους λύσεις είναι
 ή
ή  .
.Άσκηση 492
Δίνεται η συνάρτηση
 .
.α) Να υπολογίσετε το άθροισμα
 . (Μονάδες 10)
. (Μονάδες 10)β) Να βρείτε τα κοινά σημεία της γραφικής της παράστασης της
 με τους άξονες.
με τους άξονες.(Μονάδες 15)
Λύση
α)
![\displaystyle{f\text{ }\left( -1 \right)+f\left( 0 \right)+f\left( 1 \right)=\left[ {{\left( -1 \right)}^{2}}+2\left( -1 \right)-15 \right]+\left[ {{0}^{2}}+2\cdot 0-15
\right]+\left[ {{1}^{2}}+2\cdot 1-15 \right]}
=\left \displaystyle{f\text{ }\left( -1 \right)+f\left( 0 \right)+f\left( 1 \right)=\left[ {{\left( -1 \right)}^{2}}+2\left( -1 \right)-15 \right]+\left[ {{0}^{2}}+2\cdot 0-15
\right]+\left[ {{1}^{2}}+2\cdot 1-15 \right]}
=\left](/forum/ext/geomar/texintegr/latexrender/pictures/571cee57c5ef5b830dd491a8855a1a4e.png)
![\left[ 1+2\left( -1 \right)-15 \right]+\left( -15 \right)+\left[ 1+2\cdot 1-15 \right]\
=\left( 1-2-15 \right)-15+\left( 1+2-15 \right)= \left[ 1+2\left( -1 \right)-15 \right]+\left( -15 \right)+\left[ 1+2\cdot 1-15 \right]\
=\left( 1-2-15 \right)-15+\left( 1+2-15 \right)=](/forum/ext/geomar/texintegr/latexrender/pictures/cdbfc6471ffc9231cb76db2afc055d1d.png)

Για να βρούμε τα κοινά σημεία της γραφικής της παράστασης της
 με τον άξονα
με τον άξονα βάζουμε όπου
βάζουμε όπου  .
.
Επομένως το κοινό σημείο είναι το

Για να βρούμε τα κοινά σημεία της γραφικής της παράστασης της
 με τον άξονα
με τον άξονα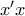 βάζουμε όπου
βάζουμε όπου  δηλαδή:
δηλαδή: 
αφού

και οι ρίζες
 ,
,Επμένως τα κοινά σημεία είναι τα
 και
και 
Άσκηση 493
α) Να λύσετε την εξίσωση
 . (Μονάδες 10)
. (Μονάδες 10)β) Να σχηματίσετε εξίσωση δευτέρου βαθμού με ρίζες, τις ρίζες της εξίσωσης του α)
ερωτήματος. (Μονάδες 15)
Λύση
α)

β) Για να βρούμε μια δευτεροβάβμια αεξίσωση ενώ ξέρουμε τις ρίζες της χρησιμοποιούμε τον τύπο

όπου

και

Άρα
 .
.Άσκηση 494
Οι διαστάσεις (σε m) του πατώματος του εργαστήριου της πληροφορικής ενός
σχολείου είναι
 και
και  , με
, με  .
.α) Να γράψετε με τη βοήθεια του
 την περίμετρο και το εμβαδόν του πατώματος. (Μονάδες 10)
την περίμετρο και το εμβαδόν του πατώματος. (Μονάδες 10)β) Αν το εμβαδόν του πατώματος του εργαστηρίου είναι
 , να βρείτε τις
, να βρείτε τιςδιαστάσεις του. (Μονάδες 15)
Λύση
Προφανώς το πάτωμα του εργαστηρίου είναι Ορθογώνιο Παραλληλόγραμμο.
α) Η περίμετρος

Το Εμβαδόν: Ε

β) Ε
 ή
ή 
αφού
 και ρίζες
και ρίζες  ,
,Όμως
 άρα
άρα  . Επομένως διαστάσεις του πατώματος του εργαστηρίου είναι
. Επομένως διαστάσεις του πατώματος του εργαστηρίου είναι  και
και .
.- Συνημμένα
-
- 491 -494.doc
- (195 KiB) Μεταφορτώθηκε 168 φορές
ΠΑΠΑΣΤΑΘΟΠΟΥΛΟΣ ΘΑΝΑΣΗΣ
Re: Λύσεις τράπεζας θεμάτων άλγεβρας σε latex
Άσκηση 485
Δίνεται η εξίσωση , με παράμετρο
, με παράμετρο  .
.
α) Να αποδείξετε ότι η παραπάνω εξίσωση γράφεται ισοδύναμα:
 (Μονάδες 8)
(Μονάδες 8)
β) Να βρείτε τις τιμές του λ για τις οποίες η παραπάνω εξίσωση έχει ακριβώς μία λύση την οποία και να βρείτε. (Μονάδες 8)
γ) Για ποια τιμή του η παραπάνω εξίσωση είναι ταυτότητα στο σύνολο των πραγματικών αριθμών; Να αιτιολογήσετε την απάντησή σας. (Μονάδες 9)
ΠΡΟΤΕΙΝΟΜΕΝΗ ΛΥΣΗ
α)



β)
Για να έχει η εξίσωση ακριβώς μία λύση πρέπει και αρκεί:
ακριβώς μία λύση πρέπει και αρκεί: 
Για την μοναδική λύση, έχουμε:
γ) Για να είναι η εξίσωση ταυτότητα στο σύνολο των πραγματικών αριθμών πρέπει και αρκεί :
ταυτότητα στο σύνολο των πραγματικών αριθμών πρέπει και αρκεί :

Δίνεται η εξίσωση
 , με παράμετρο
, με παράμετρο  .
.α) Να αποδείξετε ότι η παραπάνω εξίσωση γράφεται ισοδύναμα:
 (Μονάδες 8)
(Μονάδες 8) β) Να βρείτε τις τιμές του λ για τις οποίες η παραπάνω εξίσωση έχει ακριβώς μία λύση την οποία και να βρείτε. (Μονάδες 8)
γ) Για ποια τιμή του η παραπάνω εξίσωση είναι ταυτότητα στο σύνολο των πραγματικών αριθμών; Να αιτιολογήσετε την απάντησή σας. (Μονάδες 9)
ΠΡΟΤΕΙΝΟΜΕΝΗ ΛΥΣΗ
α)



β)
Για να έχει η εξίσωση
 ακριβώς μία λύση πρέπει και αρκεί:
ακριβώς μία λύση πρέπει και αρκεί: 
Για την μοναδική λύση, έχουμε:

γ) Για να είναι η εξίσωση
 ταυτότητα στο σύνολο των πραγματικών αριθμών πρέπει και αρκεί :
ταυτότητα στο σύνολο των πραγματικών αριθμών πρέπει και αρκεί :
Ποτε δεν κάνω λάθος! Μια φορά νομιζα πως είχα κάνει, αλλά τελικά έκανα λάθος!
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Re: Λύσεις τράπεζας θεμάτων άλγεβρας σε latex
Άσκηση 486
Αν , τότε
, τότε
α) να αποδείξετε ότι: (Μονάδες 13)
(Μονάδες 13)
β) να διατάξετε από το μικρότερο προς το μεγαλύτερο τους αριθμούς :
(Μονάδες 12)
ΠΡΟΤΕΙΝΟΜΕΝΗ ΛΥΣΗ
α) Είναι
Άρα:
β) Είναι άρα
άρα  και από το προηγούμενο ερώτημα έχουμε ότι
και από το προηγούμενο ερώτημα έχουμε ότι  , επομένως
, επομένως  . Από την υπόθεση ισχύει
. Από την υπόθεση ισχύει  και τα μέλη της ανισότητας είναι θετικά, άρα
και τα μέλη της ανισότητας είναι θετικά, άρα  .
.
Συνεπώς:
Αν
 , τότε
, τότεα) να αποδείξετε ότι:
 (Μονάδες 13)
(Μονάδες 13)β) να διατάξετε από το μικρότερο προς το μεγαλύτερο τους αριθμούς :

(Μονάδες 12)
ΠΡΟΤΕΙΝΟΜΕΝΗ ΛΥΣΗ
α) Είναι

Άρα:

β) Είναι
 άρα
άρα  και από το προηγούμενο ερώτημα έχουμε ότι
και από το προηγούμενο ερώτημα έχουμε ότι  , επομένως
, επομένως  . Από την υπόθεση ισχύει
. Από την υπόθεση ισχύει  και τα μέλη της ανισότητας είναι θετικά, άρα
και τα μέλη της ανισότητας είναι θετικά, άρα  .
. Συνεπώς:

Ποτε δεν κάνω λάθος! Μια φορά νομιζα πως είχα κάνει, αλλά τελικά έκανα λάθος!
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Re: Λύσεις τράπεζας θεμάτων άλγεβρας σε latex
Άσκηση 487
α) Να αποδείξετε ότι για οποιουσδήποτε πραγματικούς αριθμούς ισχύει:
ισχύει:
 (Μονάδες 12)
(Μονάδες 12)
β) Να βρείτε τους αριθμούς ώστε:
ώστε:  (Μονάδες 13)
(Μονάδες 13)
ΠΡΟΤΕΙΝΟΜΕΝΗ ΛΥΣΗ
α) Για οποιουσδήποτε πραγματικούς αριθμούς έχουμε:
έχουμε:



β) Είναι




α) Να αποδείξετε ότι για οποιουσδήποτε πραγματικούς αριθμούς
 ισχύει:
ισχύει: (Μονάδες 12)
(Μονάδες 12)β) Να βρείτε τους αριθμούς
 ώστε:
ώστε:  (Μονάδες 13)
(Μονάδες 13)ΠΡΟΤΕΙΝΟΜΕΝΗ ΛΥΣΗ
α) Για οποιουσδήποτε πραγματικούς αριθμούς
 έχουμε:
έχουμε:


β) Είναι




Ποτε δεν κάνω λάθος! Μια φορά νομιζα πως είχα κάνει, αλλά τελικά έκανα λάθος!
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Απ' τα τσακάλια δεν γλυτώνεις μ' ευχές η παρακάλια. Κ. Βάρναλης
Aπέναντι στις αξίες σου να είσαι ανυποχώρητος
Ενεργό μέλος από 23-12-2008 ως και 17-8-2014 (δεν θα απαντήσω σε πμ)
Re: Λύσεις τράπεζας θεμάτων άλγεβρας σε latex
Kαλησπέρα σε όλους
Το ΘΕΜΑ που κληρώθηκε σήμερα στο σχολείο μου μας δημιουργησε μια απορία στη λύση στο τελευταίο ερώτημα :
που κληρώθηκε σήμερα στο σχολείο μου μας δημιουργησε μια απορία στη λύση στο τελευταίο ερώτημα :
Χρειάζεται η μελέτη της απόστασης των ριζών όταν είναι ίσες ; Δηλαδή μηδενική απόσταση ; εννοείται ότι οι ρίζες μπορεί να είναι άνισες η να είναι ίσες
Γιάννης
ΥΓ Η λύση έχει γραφτεί παραπάνω χωρίς διερεύνηση......
Το ΘΕΜΑ
 που κληρώθηκε σήμερα στο σχολείο μου μας δημιουργησε μια απορία στη λύση στο τελευταίο ερώτημα :
που κληρώθηκε σήμερα στο σχολείο μου μας δημιουργησε μια απορία στη λύση στο τελευταίο ερώτημα :Χρειάζεται η μελέτη της απόστασης των ριζών όταν είναι ίσες ; Δηλαδή μηδενική απόσταση ; εννοείται ότι οι ρίζες μπορεί να είναι άνισες η να είναι ίσες
Γιάννης
ΥΓ Η λύση έχει γραφτεί παραπάνω χωρίς διερεύνηση......
α. Η δυσκολία με κάνει δυνατότερο.
β. Όταν πέφτεις να έχεις τη δύναμη να σηκώνεσαι.
β. Όταν πέφτεις να έχεις τη δύναμη να σηκώνεσαι.
- Christos.N
- Δημοσιεύσεις: 2105
- Εγγραφή: Πέμ Νοέμ 26, 2009 2:28 pm
- Τοποθεσία: Ίλιον
Re: Λύσεις τράπεζας θεμάτων άλγεβρας σε latex
Αφού ορίζεται ξεκάθαρα ότι οι ρίζες είναι άνισες, η απόσταση είναι μη μηδενική.STOPJOHN έγραψε:Kαλησπέρα σε όλους
Το ΘΕΜΑπου κληρώθηκε σήμερα στο σχολείο μου μας δημιουργησε μια απορία στη λύση στο τελευταίο ερώτημα :
Χρειάζεται η μελέτη της απόστασης των ριζών όταν είναι ίσες ; Δηλαδή μηδενική απόσταση ; εννοείται ότι οι ρίζες μπορεί να είναι άνισες η να είναι ίσες
Γιάννης
ΥΓ Η λύση έχει γραφτεί παραπάνω χωρίς διερεύνηση......
Χρήστος Ντάβας
Wir müssen wissen — wir werden wissen! D.Hilbert
Wir müssen wissen — wir werden wissen! D.Hilbert
Re: Λύσεις τράπεζας θεμάτων άλγεβρας σε latex
ΔΕΝ ΕΙΝΑΙ ΞΕΚΑΘΑΡΟ ΔΗΛΑΔΉ Ο ΣΥΣΧΕΤΙΣΜΟΣ ΤΩΝ ΕΡΩΤΗΜΑΤΩΝ
Γιάννης
Γιάννης
α. Η δυσκολία με κάνει δυνατότερο.
β. Όταν πέφτεις να έχεις τη δύναμη να σηκώνεσαι.
β. Όταν πέφτεις να έχεις τη δύναμη να σηκώνεσαι.
- Christos.N
- Δημοσιεύσεις: 2105
- Εγγραφή: Πέμ Νοέμ 26, 2009 2:28 pm
- Τοποθεσία: Ίλιον
Re: Λύσεις τράπεζας θεμάτων άλγεβρας σε latex
Αφού το ερώτημα υποθέτει ξεκάθαρα ότιexdx έγραψε:GI_A_ALG_4_1874
γ) Αν η εξίσωση έχει ρίζες τους αριθμούςκαι
είναι η απόσταση των
στον άξονα των πραγματικών αριθμών, να βρείτε για ποιες τιμές του ισχύει:
 , προφανώς αν είχαμε μια ρίζα διπλή δεν καλύπτεται η υπόθεση του ερωτήματος και απορρίπτεται ως λύση, αφού έχουμε μη μηδενική απόσταση.
, προφανώς αν είχαμε μια ρίζα διπλή δεν καλύπτεται η υπόθεση του ερωτήματος και απορρίπτεται ως λύση, αφού έχουμε μη μηδενική απόσταση.Εννοείς ότι πρέπει να γίνει διερεύνηση για να απορριφθεί η περίπτωση αυτή;
Χρήστος Ντάβας
Wir müssen wissen — wir werden wissen! D.Hilbert
Wir müssen wissen — wir werden wissen! D.Hilbert
- exdx
- Επιμελητής
- Δημοσιεύσεις: 1742
- Εγγραφή: Κυρ Δεκ 21, 2008 6:00 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: Λύσεις τράπεζας θεμάτων άλγεβρας σε latex
Εύλογη η απορία σου (και δική μου)
Υπέθεσα ότι είναι άνισες λόγω του προηγούμενου ερωτήματος
Πιστεύω ότι είναι άλλη μια ασάφεια - παράλειψη του θεματοδότη
Θα το δώ πάλι .
Υπέθεσα ότι είναι άνισες λόγω του προηγούμενου ερωτήματος
Πιστεύω ότι είναι άλλη μια ασάφεια - παράλειψη του θεματοδότη
Θα το δώ πάλι .
Kαλαθάκης Γιώργης
Re: Λύσεις τράπεζας θεμάτων άλγεβρας σε latex
Εννοώ για τη διερεύνηση και δεν είχαμε την απαίτηση οι μαθητές να το μελετήσουν
Γιάννης
Γιάννης
α. Η δυσκολία με κάνει δυνατότερο.
β. Όταν πέφτεις να έχεις τη δύναμη να σηκώνεσαι.
β. Όταν πέφτεις να έχεις τη δύναμη να σηκώνεσαι.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες
