 (
( , και η διχοτόμος του
, και η διχοτόμος του  . Από το
. Από το 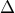
φέρνουμε την
 κάθετη στην
κάθετη στην  και ονομάζουμε
και ονομάζουμε  το σημείο στο οποίο η ευθεία
το σημείο στο οποίο η ευθεία  τέμνει την προέκταση της
τέμνει την προέκταση της 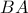 .
.Nα αποδείξετε ότι:
(α) Το τρίγωνο
 είναι ισοσκελές
είναι ισοσκελές(β) Τα τρίγωνα
 και
και  είναι ίσα
είναι ίσα(γ) Η ευθεία
 είναι μεσοκάθετη των τμημάτων
είναι μεσοκάθετη των τμημάτων  και
και 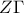
(δ) Το τετράπλευρο
 είναι ισοσκελές τραπέζιο
είναι ισοσκελές τραπέζιοΛΥΣΗ
(α) Τα ορθογώνια τρίγωνα
 και
και 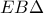 έχουν την υποτείνουσα
έχουν την υποτείνουσα  κοινή και
κοινή και 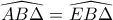 . Άρα
. Άρα είναι ίσα και άρα θα έχουν και
 , δηλαδή το τρίγωνο
, δηλαδή το τρίγωνο  είναι ισοσκελές.
είναι ισοσκελές.(β) Τα ορθογώνια τρίγωνα
 και
και  έχουν:
έχουν:  (όπως είδαμε στο (α) ερώτημα) και την γωνία
(όπως είδαμε στο (α) ερώτημα) και την γωνία  κοινή. Άρα είναι ίσα.
κοινή. Άρα είναι ίσα. (γ) Αφού το τρίγωνο
 είναι ισοσκελές και η
είναι ισοσκελές και η  είναι διχοτόμος της γωνίας
είναι διχοτόμος της γωνίας  , άρα η
, άρα η  είναι μεσοκάθετος του
είναι μεσοκάθετος του  ,
, διότι σε κάθε ισοσκελές τρίγωνο, η διχοτόμος που άγεται από την κορυφή του είναι και διάμεσος και ύψος.
Eπίσης αφού και τα τρίγωνα
 και
και  είναι ίσα (όπως δείξαμε στο (β) ερώτημα), θα έχουμε ότι
είναι ίσα (όπως δείξαμε στο (β) ερώτημα), θα έχουμε ότι 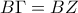 και άρα και το
και άρα και το τρίγωνο
 είναι ισοσκελές με κορυφή το
είναι ισοσκελές με κορυφή το  . Συνεπώς η διχοτόμος που άγεται από την κορυφή
. Συνεπώς η διχοτόμος που άγεται από την κορυφή  θα είναι η μεσοκάθετος του
θα είναι η μεσοκάθετος του 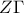
(δ) Οι ευθείες
 είναι παράλληλες ως κάθετες στην ίδια ευθεία
είναι παράλληλες ως κάθετες στην ίδια ευθεία  . Kαι εφόσον οι ευθείες
. Kαι εφόσον οι ευθείες  τέμνονται (στο
τέμνονται (στο  )
)συμπεραίνουμε ότι το τετράπλευρο
 είναι τραπέζιο. Επίσης από τα προηγούμενα ερωτήματα έχουμε ότι:
είναι τραπέζιο. Επίσης από τα προηγούμενα ερωτήματα έχουμε ότι: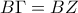

Με αφαίρεση αυτών κατά μέλη παίρνουμε :
 , οπότε το πιο πάνω τραπέζιο είναι ισοσκελές.
, οπότε το πιο πάνω τραπέζιο είναι ισοσκελές.
 (
( ) και η διχοτόμος του
) και η διχοτόμος του  . Φέρουμε από το
. Φέρουμε από το  κάθετη στην
κάθετη στην  και την πλευρά
και την πλευρά  στο
στο .
. είναι το μέσο της πλευράς
είναι το μέσο της πλευράς  , να αποδείξετε ότι:
, να αποδείξετε ότι:  είναι ισοσκελές. (Μονάδες 9)
είναι ισοσκελές. (Μονάδες 9)  (Μονάδες 8)
(Μονάδες 8)  (Μονάδες 8
(Μονάδες 8 είναι ύψος και διχοτόμος, οπότε είναι ισοσκελές.
είναι ύψος και διχοτόμος, οπότε είναι ισοσκελές. .Έτσι, από το τρίγωνο
.Έτσι, από το τρίγωνο  προκύπτει ότι
προκύπτει ότι  , διότι
, διότι  , αφού το τρίγωνο
, αφού το τρίγωνο  με
με  και το ύψος του
και το ύψος του  . Αν
. Αν  ,
,  είναι τα μέσα των
είναι τα μέσα των  ,
, και
και  αντίστοιχα, να αποδείξετε ότι :
αντίστοιχα, να αποδείξετε ότι :  είναι ισοσκελές τραπέζιο. (Μονάδες 8)
είναι ισοσκελές τραπέζιο. (Μονάδες 8) και
και  είναι ίσες . (Μονάδες 8)
είναι ίσες . (Μονάδες 8) και
και  είναι ίσες. (Μονάδες 9)
είναι ίσες. (Μονάδες 9) . Άρα
. Άρα  . Όμοια με πριν
. Όμοια με πριν  .
.  τέμνει
τέμνει  . Συνεπώς
. Συνεπώς  . Πράγματι,
. Πράγματι,  διάμεσος ορθογωνίου τριγώνου
διάμεσος ορθογωνίου τριγώνου  , άρα
, άρα  . Δηλαδή
. Δηλαδή  . Επομένως
. Επομένως  .
. ως εντός και επι τα αυτά (...).
ως εντός και επι τα αυτά (...). και
και  .
. με γωνία
με γωνία  . Φέρνουμε τα ύψη
. Φέρνουμε τα ύψη  που τέμνονται στο
που τέμνονται στο  . Φέρνουμε
. Φέρνουμε  διχοτόμο της γωνίας
διχοτόμο της γωνίας  και
και  κάθετο στο ύψος
κάθετο στο ύψος  . Να αποδείξετε ότι :
. Να αποδείξετε ότι : ισχύει
ισχύει  . (μ 9)
. (μ 9) είναι ισόπλευρο . (μ8)
είναι ισόπλευρο . (μ8) είναι ισοσκελές τραπέζιο . (μ8)
είναι ισοσκελές τραπέζιο . (μ8) είναι κάθετες στην
είναι κάθετες στην  . Στο ορθογώνιο τρίγωνο
. Στο ορθογώνιο τρίγωνο  το άθροισμα των οξειών του είναι
το άθροισμα των οξειών του είναι  , συνεπώς
, συνεπώς  . Όμως
. Όμως  γιατί έχουν κάθετες πλευρές και άρα και
γιατί έχουν κάθετες πλευρές και άρα και  . Επειδή όμως το ορθογώνιο τρίγωνο
. Επειδή όμως το ορθογώνιο τρίγωνο  έχει την οξεία του γωνία
έχει την οξεία του γωνία  η άλλη οξεία του γωνία θα είναι
η άλλη οξεία του γωνία θα είναι  και συνεπώς κάθε μια από τις ίσες , λόγω διχοτόμου, γωνίες
και συνεπώς κάθε μια από τις ίσες , λόγω διχοτόμου, γωνίες  θα είναι από
θα είναι από  , δηλαδή :
, δηλαδή :  .
. η γωνία
η γωνία  είναι εξωτερική του και άρα
είναι εξωτερική του και άρα 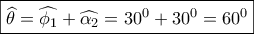 . Μετά απ αυτά αβίαστα προκύπτουν:
. Μετά απ αυτά αβίαστα προκύπτουν:  κάθετη πλευρά ορθογωνίου τριγώνου με απέναντι γωνία
κάθετη πλευρά ορθογωνίου τριγώνου με απέναντι γωνία 
 είναι ισόπλευρα γιατί έχουν από 2 γωνίες ίσες με
είναι ισόπλευρα γιατί έχουν από 2 γωνίες ίσες με  είναι ίσες, από
είναι ίσες, από  και
και  τα ύψη του. Να αποδείξετε ότι:
τα ύψη του. Να αποδείξετε ότι: 



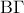 του ισοσκελούς τριγώνου είναι και διάμεσος, δηλαδή το
του ισοσκελούς τριγώνου είναι και διάμεσος, δηλαδή το  το
το  είναι διάμεσος στην υποτείνουσα
είναι διάμεσος στην υποτείνουσα  .
.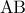 φαίνεται από τις απέναντι κορυφές
φαίνεται από τις απέναντι κορυφές  υπό ορθή γωνία.
υπό ορθή γωνία.
 ως οξείες γωνίες με κάθετες πλευρές και επειδή
ως οξείες γωνίες με κάθετες πλευρές και επειδή 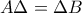 θα ισχύει για τις γωνίες
θα ισχύει για τις γωνίες  άρα
άρα 
 .
. στα χίλια να σου ζητήσουν το λόγο, το γιατί, προφανές.
στα χίλια να σου ζητήσουν το λόγο, το γιατί, προφανές.
 και δύο ομόκεντροι κύκλοι
και δύο ομόκεντροι κύκλοι  και
και  με
με  , που τέμνουν την
, που τέμνουν την  στα σημεία
στα σημεία  ,
,
 στα
στα  αντίστοιχα. Να αποδείξετε ότι:
αντίστοιχα. Να αποδείξετε ότι: . (Μονάδες 8)
. (Μονάδες 8) είναι ισοσκελές, όπου
είναι ισοσκελές, όπου  το σημείο τομής των
το σημείο τομής των  και
και  . (Μονάδες 8)
. (Μονάδες 8)  διχοτομεί την γωνία
διχοτομεί την γωνία  (Μονάδες 9)
(Μονάδες 9)
 και
και  . Έχουν:
. Έχουν:  (ΠΓΠ). Άρα,
(ΠΓΠ). Άρα,  (1)
(1) και
και  . Έχουν:
. Έχουν: 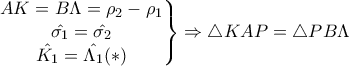 (ΓΠΓ)
(ΓΠΓ) ισχύει λόγω (1),
ισχύει λόγω (1),  (κατακορυφήν) και άθροισμα γωνιών τριγώνου
(κατακορυφήν) και άθροισμα γωνιών τριγώνου 
 (2), δηλ.
(2), δηλ. 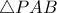 ισοσκελές.
ισοσκελές. και
και  . Έχουν:
. Έχουν:  (ΠΠΠ). Άρα,
(ΠΠΠ). Άρα,  δηλ. ΟΡ διχοτόμος
δηλ. ΟΡ διχοτόμος  .
. .
. μόνο και
μόνο και 
 , και τυχαίο σημείο
, και τυχαίο σημείο  της πλευράς
της πλευράς  .
.  και
και 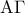 στα σημεία
στα σημεία  και
και 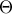 αντίστοιχα.
αντίστοιχα. 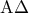 και
και  τα ύψη των τριγώνων
τα ύψη των τριγώνων  και
και αντίστοιχα, να αποδείξετε ότι:
αντίστοιχα, να αποδείξετε ότι:  (Μονάδες 8)
(Μονάδες 8)  (Μονάδες 9)
(Μονάδες 9) είναι ορθογώνιο αφού έχει τρεις ορθές γωνίες.
είναι ορθογώνιο αφού έχει τρεις ορθές γωνίες.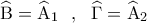 κι αφού
κι αφού  έχουμε ότι η
έχουμε ότι η  είναι διχοτόμος της
είναι διχοτόμος της 
 είναι ταυτόχρονα διχοτόμος και ύψος .
είναι ταυτόχρονα διχοτόμος και ύψος . .
.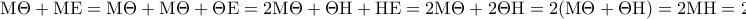
 και δυο μη αντιδιαμετρικά σημεία του
και δυο μη αντιδιαμετρικά σημεία του  και
και  .
.  .
.  του τριγώνου
του τριγώνου  είναι ισοσκελές.
είναι ισοσκελές.  είναι ρόμβος.
είναι ρόμβος.  είναι συνευθειακά.
είναι συνευθειακά.  ως εφαπτόμενα τμήματα, δηλαδή το τρίγωνο
ως εφαπτόμενα τμήματα, δηλαδή το τρίγωνο  είναι ισοσκελές.
είναι ισοσκελές. και
και  είναι ίσα αφού έχουν την πλευρά
είναι ίσα αφού έχουν την πλευρά 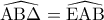 ως προσκείμενες στη βάση του ισοσκελούς τριγώνου
ως προσκείμενες στη βάση του ισοσκελούς τριγώνου  , οπότε το τρίγωνο
, οπότε το τρίγωνο 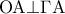 και
και  έτσι
έτσι 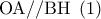
 ως κάθετες στην
ως κάθετες στην  .
. ως ακτίνες του κύκλου.
ως ακτίνες του κύκλου.
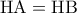 από το ισοσκελές τρίγωνο
από το ισοσκελές τρίγωνο  και
και 
 και στην προέκταση της
και στην προέκταση της  (προς το
(προς το  ενώ στην προέκταση της
ενώ στην προέκταση της  .
.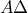 και
και 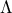 αντίστοιχα, και η
αντίστοιχα, και η  τέμνει τις
τέμνει τις  αντίστοιχα να αποδείξετε ότι:
αντίστοιχα να αποδείξετε ότι: )
) και
και  είναι ισοσκελή (Μονάδες
είναι ισοσκελή (Μονάδες  )
) (Μονάδες
(Μονάδες  είναι ισοσκελή οι διχοτόμοι
είναι ισοσκελή οι διχοτόμοι  των γωνιών
των γωνιών  αντίστοιχα, θα είναι και διάμεσοι.
αντίστοιχα, θα είναι και διάμεσοι. του τριγώνου
του τριγώνου  , άρα
, άρα  .
. και
και  (ως εντός εκτός και επί τα αυτά)
(ως εντός εκτός και επί τα αυτά) και
και  .
. και
και  , δηλαδή τα τρίγωνα
, δηλαδή τα τρίγωνα  θα διέρχεται από τα μέσα των πλευρών
θα διέρχεται από τα μέσα των πλευρών 
 είναι τα μέσα των
είναι τα μέσα των 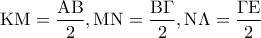 .
.

 και
και  . Φέρνουμε κάθετη στην
. Φέρνουμε κάθετη στην  στο σημείο της
στο σημείο της  .
.
 είναι ισοσκελές.
είναι ισοσκελές.
 και
και  είναι ίσα γιατι η
είναι ίσα γιατι η  αφου το
αφου το  και
και 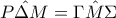 ώς εντός εναλλάξ και
ώς εντός εναλλάξ και  ώς κατακορυφήν. Άρα
ώς κατακορυφήν. Άρα 
 άρα το τρίγωνο
άρα το τρίγωνο  όμως
όμως 