
2. α) Να αποδειχθεί ότι κάθε ν-οστή ρίζα της μονάδας είναι της μορφής
 .
.β) Να λυθεί η εξίσωση στο σύνολο
 των μιγαδικών
των μιγαδικών .
.3. α) Να αποδειχθεί ότι αν η συνάρτηση
 είναι παραγωγίσιμη σε ένα διάστημα
είναι παραγωγίσιμη σε ένα διάστημα 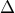
και για κάθε
 είναι
είναι  τότε η συνάρτηση
τότε η συνάρτηση  είναι σταθερή στο
είναι σταθερή στο 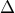 .
.β) Έστω
 συναρτήσεις με πεδίο ορισμού ένα διάστημα
συναρτήσεις με πεδίο ορισμού ένα διάστημα 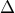 για τις οποίες υποθέτουμε ότι :
για τις οποίες υποθέτουμε ότι : είναι δυο φορές παραγωγίσιμες στο
είναι δυο φορές παραγωγίσιμες στο 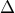

 και
και 
 και
και 
Να δειχθεί ότι :
i) Για κάθε
 όπου
όπου 
ii) Αν η
 έχει δυο ρίζες ετερόσημες
έχει δυο ρίζες ετερόσημες  τότε η
τότε η  έχει τουλάχιστον μία ρίζα στο κλειστό διάστημα
έχει τουλάχιστον μία ρίζα στο κλειστό διάστημα ![\left[ {{\rho }_{1}},{{\rho }_{2}} \right] \left[ {{\rho }_{1}},{{\rho }_{2}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/a48e7024b3c145e04e3c7a5656704479.png) .
.4. Δίνεται η συνάρτηση
 με
με  και πεδίο ορισμού το διάστημα
και πεδίο ορισμού το διάστημα ![\displaystyle{\left[ -\frac{\pi }{4},\frac{\pi }{4} \right]} \displaystyle{\left[ -\frac{\pi }{4},\frac{\pi }{4} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/62defcfc53c3d8e2993ebbe17319ab89.png) .
.α) Να βρεθεί η εξίσωση της εφαπτομένης της γραφικής παράστασης της
 στο σημείο
στο σημείο  .
.β) Να υπολογιστεί το εμβαδόν του χωρίου που περικλείεται από την παραπάνω εφαπτομένη,
τη γραφική παράσταση της
 και τους θετικούς ημιάξονες
και τους θετικούς ημιάξονες  .
.


 η
η  ισοδυναμεί με την :
ισοδυναμεί με την :

 (απορρίπτεται) ,
(απορρίπτεται) ,  (απορρίπτεται )
(απορρίπτεται ) 
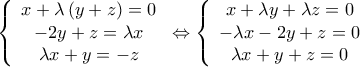


 .
. , το σύστημα έχει μοναδική λύση , τη μηδενική .
, το σύστημα έχει μοναδική λύση , τη μηδενική . , τότε γίνεται :
, τότε γίνεται :

 , γίνεται :
, γίνεται :

 , για κάθε
, για κάθε  . Άρα
. Άρα  και άρα
και άρα , για κάθε
, για κάθε 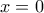 , έχουμε
, έχουμε 
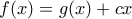 , για κάθε
, για κάθε  και
και  , όπου
, όπου 
 , τότε θα είναι και
, τότε θα είναι και  και άρα
και άρα  , δηλαδή η
, δηλαδή η  έχει ρίζες τις
έχει ρίζες τις
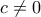 , τότε
, τότε  . Άρα από το θεώρημα Bolzano, έχουμε ότι
. Άρα από το θεώρημα Bolzano, έχουμε ότι  .
.![\displaystyle{[p_1 , p_2 ]} \displaystyle{[p_1 , p_2 ]}](/forum/ext/geomar/texintegr/latexrender/pictures/3ab3934e289a11ce33a145bd0256ff66.png) .
. η οποία είναι συνεχής, έχουμε:
η οποία είναι συνεχής, έχουμε: ![f(x)=sin(\frac{\pi }{2}+2x)=sin(\frac{\pi }{2}-(-2x))=cos(-2x)=cos2x, x\in [-\frac{\pi }{4},\frac{\pi }{4}] f(x)=sin(\frac{\pi }{2}+2x)=sin(\frac{\pi }{2}-(-2x))=cos(-2x)=cos2x, x\in [-\frac{\pi }{4},\frac{\pi }{4}]](/forum/ext/geomar/texintegr/latexrender/pictures/f60aaed2c09eb3037fece5111100713d.png)
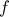 έχουμε:
έχουμε:  σχέση
σχέση 




 όπου
όπου  και
και  είναι τα σημεία τομής της εφαπτομένης με τον άξονα
είναι τα σημεία τομής της εφαπτομένης με τον άξονα  και
και  αντιστοίχως.
αντιστοίχως.![E=\frac{1}{2}(O\Gamma ).(O\Delta )-\int_{0}^{\frac{\pi }{4}}cos(2x)dx=\frac{1}{2}(\frac{\pi }{8}+\frac{1}{2}).(\frac{\pi \sqrt{2}}{8}+\frac{\sqrt{2}}{2})-[\frac{1}{2}sin(2x)]=\frac{\sqrt{2}}{2}(\frac{\pi }{8}+\frac{1}{2})^2-\frac{1}{2} E=\frac{1}{2}(O\Gamma ).(O\Delta )-\int_{0}^{\frac{\pi }{4}}cos(2x)dx=\frac{1}{2}(\frac{\pi }{8}+\frac{1}{2}).(\frac{\pi \sqrt{2}}{8}+\frac{\sqrt{2}}{2})-[\frac{1}{2}sin(2x)]=\frac{\sqrt{2}}{2}(\frac{\pi }{8}+\frac{1}{2})^2-\frac{1}{2}](/forum/ext/geomar/texintegr/latexrender/pictures/e3adee3a223f3ff19adee4e26c185314.png)



 το σύστημα έχει μοναδική λύση την
το σύστημα έχει μοναδική λύση την 
 το σύστημα έχει φανερά την απειρία λύσεων
το σύστημα έχει φανερά την απειρία λύσεων 
 το σύστημα έχει φανερά την απειρία λύσεων
το σύστημα έχει φανερά την απειρία λύσεων 