θα ανεβάσω τα υπόλοιπα της Α΄ Δέσμης με την σειρά (μένουν τα 1996-2001),
ώστε να μην υπάρχουν αρκετά άλυτα στο Ευρετήριο Θεμάτων Πανελλαδικών Εξετάσεων .
1. α) Να αποδείξετε ότι αν υπάρχει μια αρχική συνάρτηση
 της
της  σ’ ένα διάστημα
σ’ ένα διάστημα 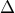 τότε υπάρχουν άπειρες
τότε υπάρχουν άπειρες και μάλιστα είναι όλες οι συναρτήσεις της μορφής
 και μόνο αυτές.
και μόνο αυτές.β) Να βρείτε την εξίσωση της ευθείας που διέρχεται από το κέντρο του κύκλου

και είναι κάθετη στην ευθεία
 .
.2. Δίνεται η συνάρτηση
 όπου η παράμετρος
όπου η παράμετρος  είναι ένας πραγματικός αριθμός.
είναι ένας πραγματικός αριθμός.Μια επιχείρηση έχει έσοδα
 που δίνονται σε εκατομμύρια δραχμές από τον τύπο
που δίνονται σε εκατομμύρια δραχμές από τον τύπο 
όπου
 συμβολίζει το χρόνο σε έτη.
συμβολίζει το χρόνο σε έτη.Το κόστος λειτουργίας
 της επιχείρησης δίνεται επίσης σε εκατομμύρια δραχμές σύμφωνα με τον τύπο
της επιχείρησης δίνεται επίσης σε εκατομμύρια δραχμές σύμφωνα με τον τύπο  .
.α) Να βρείτε τη συνάρτηση κέρδους
 για
για  όταν γνωρίζουμε ότι κατά το πρώτο έτος λειτουργίας
όταν γνωρίζουμε ότι κατά το πρώτο έτος λειτουργίας η επιχείρηση παρουσίασε ζημιά δώδεκα εκατομμύρια δραχμές.
β) Ποια χρονική στιγμή θα αρχίσει η επιχείρηση να παρουσιάζει κέρδη;
γ) Ποιος θα είναι ο ρυθμός μεταβολής της συνάρτησης κέρδους στο τέλος του δεύτερου έτους;
δ) Να υπολογίσετε την τιμή του ολοκληρώματος
 .
.3. Δίνεται η συνάρτηση
 όπου
όπου 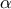 πραγματικός αριθμός μεγαλύτερος του
πραγματικός αριθμός μεγαλύτερος του 
α) Να δείξετε ότι

β) Να μελετήσετε ως προς τα ακρότατα τη συνάρτηση

γ) Αν
 είναι ρίζα της πρώτης παραγώγου και
είναι ρίζα της πρώτης παραγώγου και  είναι ρίζα της δευτέρας παραγώγου της
είναι ρίζα της δευτέρας παραγώγου της  να βρείτε τη σχέση που συνδέει τα
να βρείτε τη σχέση που συνδέει τα 
δ) Να υπολογίσετε το ολοκλήρωμα
 όταν
όταν 
4. Δίνεται ο πίνακας
![\displaystyle{A=\left[ \begin{matrix}
3 & 2 & 3 \\
0 & \lambda +1 & 2 \\
0 & \lambda -1 & \lambda +2 \\
\end{matrix} \right]} \displaystyle{A=\left[ \begin{matrix}
3 & 2 & 3 \\
0 & \lambda +1 & 2 \\
0 & \lambda -1 & \lambda +2 \\
\end{matrix} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/2597b2567a21827a2092a648079a4095.png) και οι πολυωνυμικές συναρτήσεις
και οι πολυωνυμικές συναρτήσεις 
και
 όπου
όπου  και
και  πραγματικοί αριθμοί.
πραγματικοί αριθμοί.α) Ο δειγματικός χώρος ενός πειράματος τύχης είναι
 με
με  όπου
όπου  είναι οι ρίζες της εξίσωσης
είναι οι ρίζες της εξίσωσης 
Οι πιθανότητες των στοιχειωδών ενδεχομένων ικανοποιούν τις σχέσεις

Να υπολογίσετε τις πιθανότητες των στοιχειωδών ενδεχομένων του
 .
.β) Θεωρούμε το ενδεχόμενο
 το σύστημα
το σύστημα  έχει και μη μηδενικές λύσεις
έχει και μη μηδενικές λύσεις 
όπου
 ένας
ένας  άγνωστος πίνακας και
άγνωστος πίνακας και  ο δειγματικός χώρος του (α) ερωτήματος.
ο δειγματικός χώρος του (α) ερωτήματος. Να υπολογίσετε την πιθανότητα
 .
.γ) Να δείξετε ότι για το ενδεχόμενο
 του
του  όπου
όπου  η
η  παρουσιάζει ακρότατο στο
παρουσιάζει ακρότατο στο 
και
 ο δειγματικός χώρος του (α) ερωτήματος ισχύει
ο δειγματικός χώρος του (α) ερωτήματος ισχύει  .
.δ) Να βρείτε τις πιθανότητες των ενδεχομένων
 και
και 

 άρα ο κύκλος έχει κέντρο το
άρα ο κύκλος έχει κέντρο το  . Η δοσμένη ευθεία έχει συντελεστή διεύθυνσης
. Η δοσμένη ευθεία έχει συντελεστή διεύθυνσης άρα η κάθετη σε αυτήν θα έχει
άρα η κάθετη σε αυτήν θα έχει  και εξίσωση
και εξίσωση 








 και
και 
![X = \left[ {\begin{array}{*{20}{c}}
x\\
y\\
z
\end{array}} \right] X = \left[ {\begin{array}{*{20}{c}}
x\\
y\\
z
\end{array}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/9f80bf691e800dbc87582010a1aa72d5.png) τότε:
τότε:![AX = 2X \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
3&2&3\\
0&{\lambda + 1}&2\\
0&{\lambda - 1}&{\lambda + 2}
\end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}}
x\\
y\\
z
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{2x}\\
{2y}\\
{2z}
\end{array}} \right] \Leftrightarrow AX = 2X \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
3&2&3\\
0&{\lambda + 1}&2\\
0&{\lambda - 1}&{\lambda + 2}
\end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}}
x\\
y\\
z
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{2x}\\
{2y}\\
{2z}
\end{array}} \right] \Leftrightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/974f44dad3e60174aebb3339a898b87d.png)



 οπότε
οπότε 
 , αφού είναι τριώνυμο με
, αφού είναι τριώνυμο με  , παρουσιάζει ελάχιστο για
, παρουσιάζει ελάχιστο για 
 οπότε
οπότε 

 δηλαδή
δηλαδή 
 δηλαδή
δηλαδή 
 όπου
όπου 


 την τιμή για
την τιμή για  τότε μας δίνει
τότε μας δίνει  συνεπώς
συνεπώς 
![\displaystyle{h'(x)=[2^{12}(e^{-4x}-e^{\alpha x})]' = 2^{12}[(e^{-4x})'-(e^{-\alpha x})']=2^{12}(\alpha e^{-\alpha x}-4e^{-4x})} \displaystyle{h'(x)=[2^{12}(e^{-4x}-e^{\alpha x})]' = 2^{12}[(e^{-4x})'-(e^{-\alpha x})']=2^{12}(\alpha e^{-\alpha x}-4e^{-4x})}](/forum/ext/geomar/texintegr/latexrender/pictures/214c27a22811dadd8053ad0083f8dec6.png)




![\displaystyle{\alpha > 4\xrightarrow[gn afksousa]{ln}ln\alpha > ln4} \displaystyle{\alpha > 4\xrightarrow[gn afksousa]{ln}ln\alpha > ln4}](/forum/ext/geomar/texintegr/latexrender/pictures/e2942ffaec5e5df085d33cf881feecee.png) οπότε
οπότε 


![\displaystyle{[0,\frac{ln\alpha -ln4}{\alpha -4}]} \displaystyle{[0,\frac{ln\alpha -ln4}{\alpha -4}]}](/forum/ext/geomar/texintegr/latexrender/pictures/acedda321374c3ad531f6335c52d9b64.png) και γνησίως φθίνουσα στο
και γνησίως φθίνουσα στο  συνεπώς η συνάρτηση
συνεπώς η συνάρτηση 





 που είναι και η ζητούμενη σχέση.
που είναι και η ζητούμενη σχέση.
![\displaystyle{\frac{334}{75}.2^{12}\int_{0}^{ln2}(e^{-4x}-e^{-8x})dx = \frac{334}{75}.2^{12}[-\frac{1}{4}e^{-4x}-(-\frac{1}{8}e^{-8x})]_{0}^{ln2}=...=2004} \displaystyle{\frac{334}{75}.2^{12}\int_{0}^{ln2}(e^{-4x}-e^{-8x})dx = \frac{334}{75}.2^{12}[-\frac{1}{4}e^{-4x}-(-\frac{1}{8}e^{-8x})]_{0}^{ln2}=...=2004}](/forum/ext/geomar/texintegr/latexrender/pictures/9453d64c88f552f2cc4966f842af2a67.png)

 Η συνάρτηση εσόδων είναι:
Η συνάρτηση εσόδων είναι:

 είναι :
είναι : 




 η μόνη δεκτή λύση μεταξύ των δύο είναι η
η μόνη δεκτή λύση μεταξύ των δύο είναι η 
 εφόσον
εφόσον  Δηλαδή
Δηλαδή ![\displaystyle{P'(t)=[2(t^{2}-t-6)]' = 2(2t-1)} \displaystyle{P'(t)=[2(t^{2}-t-6)]' = 2(2t-1)}](/forum/ext/geomar/texintegr/latexrender/pictures/11c804613bf849317b52824e2177867e.png) Οπότε
Οπότε που είναι και ο ζητούμενος ρυθμός μεταβολής.
που είναι και ο ζητούμενος ρυθμός μεταβολής.
![\displaystyle{111[\frac{t^{3}}{3}-\frac{t^{2}}{2}-6t]^{6}_{0}=111(\frac{6^{3}}{3}-\frac{6^{2}}{2}-36)=111.36(2-\frac{1}{2}-1)=111.36.\frac{1}{2}=1998} \displaystyle{111[\frac{t^{3}}{3}-\frac{t^{2}}{2}-6t]^{6}_{0}=111(\frac{6^{3}}{3}-\frac{6^{2}}{2}-36)=111.36(2-\frac{1}{2}-1)=111.36.\frac{1}{2}=1998}](/forum/ext/geomar/texintegr/latexrender/pictures/9f538cecd9146eb8e83d80083cd23d46.png)