Όταν σχεδόν λυθούν τα θέματα της Δ΄Δέσμης θα συνεχίσω με τα εναπομείναντα της Α΄Δέσμης (1996-2001).
1. α) Να αποδείξετε ότι, αν μία συνάρτηση
 είναι συνεχής στο κλειστό διάστημα
είναι συνεχής στο κλειστό διάστημα ![\displaystyle{[\alpha,\beta]} \displaystyle{[\alpha,\beta]}](/forum/ext/geomar/texintegr/latexrender/pictures/376cdf5202face25e8fbeaa3c1f64531.png) και
και  ,
, τότε για κάθε αριθμό
 μεταξύ των
μεταξύ των  και
και  υπάρχει τουλάχιστον ένας
υπάρχει τουλάχιστον ένας  τέτοιος ώστε να ισχύει
τέτοιος ώστε να ισχύει  .
.β) Να αποδείξετε ότι:
i ) Η συνάρτηση
 είναι γνησίως αύξουσα.
είναι γνησίως αύξουσα.ii) Η εξίσωση
 έχει μία μόνο ρίζα στο διάστημα
έχει μία μόνο ρίζα στο διάστημα  .
.2. α) Δίνεται το σύστημα
 με
με 
i. Να βρείτε την τιμή του
 για την οποία το σύστημα έχει δύο τουλάχιστον διαφορετικές λύσεις.
για την οποία το σύστημα έχει δύο τουλάχιστον διαφορετικές λύσεις.ii. Αν
 και
και  είναι δύο διαφορετικές λύσεις του συστήματος, να αποδείξετε ότι
είναι δύο διαφορετικές λύσεις του συστήματος, να αποδείξετε ότι  .
.β) Θεωρούμε στο καρτεσιανό επίπεδο
 τη γραμμή με εξίσωση
τη γραμμή με εξίσωση 
i) Να αποδείξετε ότι η προηγούμενη εξίσωση παριστάνει κύκλο και να προσδιορίσετε το κέντρο και την ακτίνα του.
ii) Να αποδείξετε ότι τα σημεία
 και
και  είναι τα άκρα μιας διαμέτρου του κύκλου.
είναι τα άκρα μιας διαμέτρου του κύκλου.3. α) Η συνάρτηση
 έχει συνεχή παράγωγο και ικανοποιεί την ισότητα
έχει συνεχή παράγωγο και ικανοποιεί την ισότητα  όπου
όπου  με
με  .
. Να αποδείξετε ότι:
i)

ii) Η εξίσωση
 έχει μία τουλάχιστον ρίζα στο διάστημα
έχει μία τουλάχιστον ρίζα στο διάστημα  .
.β) Έστω η συνάρτηση

i) Να αποδείξετε ότι το εμβαδόν
 του χωρίου που περικλείεται από τη γραφική παράσταση της συνάρτησης
του χωρίου που περικλείεται από τη γραφική παράσταση της συνάρτησης  ,
, τον άξονα
 και τις ευθείες
και τις ευθείες  , όπου
, όπου  , είναι
, είναι 
ii) Να προσδιορίσετε την τιμή του
 για την οποία το εμβαδόν
για την οποία το εμβαδόν  γίνεται ελάχιστο.
γίνεται ελάχιστο.4. α) Δίνεται η συνάρτηση

i) Να αποδείξετε ότι
 .
.ii) Να βρείτε την εξίσωση της εφαπτομένης της γραφικής παράστασης της συνάρτησης
 στο σημείο
στο σημείο  .
.β) Έστω η συνάρτηση
 όπου
όπου  .
.i) Αν η ευθεία
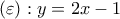 είναι ασύμπτωτη της γραφικής παράστασης της
είναι ασύμπτωτη της γραφικής παράστασης της  στο
στο  , ποιες είναι οι τιμές των
, ποιες είναι οι τιμές των  ;
;ii) Έστω
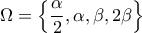 είναι ένας δειγματικός χώρος με ισοπίθανα απλά ενδεχόμενα,
είναι ένας δειγματικός χώρος με ισοπίθανα απλά ενδεχόμενα, όπου οι
 έχουν τις τιμές που προκύπτουν στο προηγούμενο ερώτημα.
έχουν τις τιμές που προκύπτουν στο προηγούμενο ερώτημα.Θεωρούμε τη συνάρτηση

και το ενδεχόμενο
 η συνάρτηση
η συνάρτηση  είναι κυρτή στο
είναι κυρτή στο 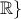
Να βρείτε την πιθανότητα του ενδεχομένου
 .
.
 έχουμε
έχουμε![\displaystyle{f^\prime(x)=3x^2+2-2\,\sigma \upsilon \nu\,2x=3x^2+2\left[1-\sigma \upsilon \nu\,\left(2x\right)\right]=3x^2+4\,\eta \mu^2\,x\geq 0} \displaystyle{f^\prime(x)=3x^2+2-2\,\sigma \upsilon \nu\,2x=3x^2+2\left[1-\sigma \upsilon \nu\,\left(2x\right)\right]=3x^2+4\,\eta \mu^2\,x\geq 0}](/forum/ext/geomar/texintegr/latexrender/pictures/7149427e1a29a51db3a812776883476f.png)
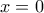

![\displaystyle{x\in\left[0,1\right]} \displaystyle{x\in\left[0,1\right]}](/forum/ext/geomar/texintegr/latexrender/pictures/3c1b4eb4b37cab2818a774ee2e10818c.png) είναι,
είναι,
![\displaystyle{\left[0,1\right]} \displaystyle{\left[0,1\right]}](/forum/ext/geomar/texintegr/latexrender/pictures/8a9ad5969c392fbad7e61ac2ad452bbe.png) και
και  ,
, , από το Θεώρημα του Bolzano, έπεται ότι υπάρχει
, από το Θεώρημα του Bolzano, έπεται ότι υπάρχει τέτοιο, ώστε
τέτοιο, ώστε  , που είναι και μοναδικό, λόγω μονοτονίας
, που είναι και μοναδικό, λόγω μονοτονίας![\displaystyle{g(x)=\int_{0}^{x}x\,\sigma \upsilon \nu\,t\,dt=x\int_{0}^{x}\sigma \upsilon \nu\,t\,dt=x\left[\eta \mu\,t\right]_{0}^{x}=x\,\eta \mu\,x} \displaystyle{g(x)=\int_{0}^{x}x\,\sigma \upsilon \nu\,t\,dt=x\int_{0}^{x}\sigma \upsilon \nu\,t\,dt=x\left[\eta \mu\,t\right]_{0}^{x}=x\,\eta \mu\,x}](/forum/ext/geomar/texintegr/latexrender/pictures/cc88c48bd49b5372badc577ad1aea4dc.png)

 είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο 
 , δίνεται από τη σχέση,
, δίνεται από τη σχέση,
 είναι η ασύμπτωτη του γραφήματος της συνάρτησης
είναι η ασύμπτωτη του γραφήματος της συνάρτησης 




 .
.![\displaystyle{\begin{aligned} g''(x)=x^2-2\left(\lambda-1\right)x+4&=\left[x-\left(\lambda-1\right)\right]^2+4-\left(\lambda-1\right)^2\\&=\left[x-\left(\lambda-1\right)\right]^2+\left[2-\left(\lambda-1\right)\right]\left[2+\left(\lambda-1\right)\right]\\&=\left[x-\left(\lambda-1\right)\right]^2+\left(3-\lambda\right)\left(1+\lambda\right)\end{aligned}} \displaystyle{\begin{aligned} g''(x)=x^2-2\left(\lambda-1\right)x+4&=\left[x-\left(\lambda-1\right)\right]^2+4-\left(\lambda-1\right)^2\\&=\left[x-\left(\lambda-1\right)\right]^2+\left[2-\left(\lambda-1\right)\right]\left[2+\left(\lambda-1\right)\right]\\&=\left[x-\left(\lambda-1\right)\right]^2+\left(3-\lambda\right)\left(1+\lambda\right)\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/19c0e0c6ef1beb513fdc75bc76cfa4dd.png)
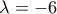 , τότε
, τότε ![\displaystyle{g''(x)=\left(x+7\right)^2-45=\left(x+7-\sqrt{45}\right)\left(x+7+\sqrt{45}\right)<0\ \forall x\in\left[-7-\sqrt{45},\sqrt{45}-7\right]} \displaystyle{g''(x)=\left(x+7\right)^2-45=\left(x+7-\sqrt{45}\right)\left(x+7+\sqrt{45}\right)<0\ \forall x\in\left[-7-\sqrt{45},\sqrt{45}-7\right]}](/forum/ext/geomar/texintegr/latexrender/pictures/12c2d937cd4f661300c69cea05a59bb9.png)
 , τότε
, τότε ![\displaystyle{g''(x)=\left(x+4\right)^2-12=\left(x+4+2\sqrt{3}\right)\left(x+4-2\sqrt{3}\right)<0\ \forall x\in\left[-4-2\sqrt{3},2\sqrt{3}-4\right]} \displaystyle{g''(x)=\left(x+4\right)^2-12=\left(x+4+2\sqrt{3}\right)\left(x+4-2\sqrt{3}\right)<0\ \forall x\in\left[-4-2\sqrt{3},2\sqrt{3}-4\right]}](/forum/ext/geomar/texintegr/latexrender/pictures/0efd3966ef151ec24cc20ba50e25ecea.png)
 , τότε
, τότε 
 , τότε
, τότε 
 και άρα
και άρα 
![\displaystyle{\begin{aligned} \forall x\in\mathbb{R}:g''(x)>0&\Leftrightarrow \forall x\in\mathbb{R}:\left[x-\left(\lambda-1\right)\right]^2+\left(3-\lambda\right)\left(1+\lambda\right)>0\\&\Leftrightarrow \left(3-\lambda\right)\left(\lambda+1\right)>0\\&\Leftrightarrow \left[3-\lambda>0\ \land \lambda+1>0\right]\ \lor \left[3-\lambda<0\ \land \lambda+1<0\right]\\&\Leftrightarrow \left[\lambda<3\ \land \lambda>-1\right]\ \lor \left[\lambda>3\ \land \lambda<-1\right]\\&\Leftrightarrow \lambda\in\left(-1,3\right)\cup \varnothing\\&\Leftrightarrow \lambda\in\left(-1,3\right)\\&\Leftrightarrow \lambda\in\left\{1,2\right\}\end{aligned}} \displaystyle{\begin{aligned} \forall x\in\mathbb{R}:g''(x)>0&\Leftrightarrow \forall x\in\mathbb{R}:\left[x-\left(\lambda-1\right)\right]^2+\left(3-\lambda\right)\left(1+\lambda\right)>0\\&\Leftrightarrow \left(3-\lambda\right)\left(\lambda+1\right)>0\\&\Leftrightarrow \left[3-\lambda>0\ \land \lambda+1>0\right]\ \lor \left[3-\lambda<0\ \land \lambda+1<0\right]\\&\Leftrightarrow \left[\lambda<3\ \land \lambda>-1\right]\ \lor \left[\lambda>3\ \land \lambda<-1\right]\\&\Leftrightarrow \lambda\in\left(-1,3\right)\cup \varnothing\\&\Leftrightarrow \lambda\in\left(-1,3\right)\\&\Leftrightarrow \lambda\in\left\{1,2\right\}\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/fa3b0d91babe15d3f08b41e3dfef49cb.png)
 είναι ένα τριώνυμο του
είναι ένα τριώνυμο του  με θετικό συντελεστή του
με θετικό συντελεστή του  ,
,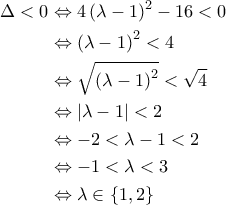
 :
: 

![\displaystyle{\Leftrightarrow [e^{f(x)}]_{\alpha }^{\beta } = 0 \Leftrightarrow e^{f(\beta )}-e^{f(\alpha )} = 0 \Leftrightarrow e^{f(\beta )} = e^{f(\alpha )}\overset{e^{f}>0}{\rightarrow} } \displaystyle{\Leftrightarrow [e^{f(x)}]_{\alpha }^{\beta } = 0 \Leftrightarrow e^{f(\beta )}-e^{f(\alpha )} = 0 \Leftrightarrow e^{f(\beta )} = e^{f(\alpha )}\overset{e^{f}>0}{\rightarrow} }](/forum/ext/geomar/texintegr/latexrender/pictures/b86e9b76f648ff3d8d9c5de9ff9e03fc.png)

![\displaystyle{[\alpha ,\beta ]} \displaystyle{[\alpha ,\beta ]}](/forum/ext/geomar/texintegr/latexrender/pictures/495a1910d13927c0bd1cea021aee0023.png)

 από το προηγούμενο ερώτημα
από το προηγούμενο ερώτημα  δηλαδή
δηλαδή  ρίζα της
ρίζα της 
 .
.


![\displaystyle{\int_{\lambda }^{\lambda +1}(x^{2})'dx + 4\int_{\lambda }^{\lambda +1}(lnx)'dx = [x^{2}+4lnx]_{\lambda } ^{\lambda +1} =} \displaystyle{\int_{\lambda }^{\lambda +1}(x^{2})'dx + 4\int_{\lambda }^{\lambda +1}(lnx)'dx = [x^{2}+4lnx]_{\lambda } ^{\lambda +1} =}](/forum/ext/geomar/texintegr/latexrender/pictures/26d412cab8e0556c434632805d6693f5.png)


 έτσι ώστε το εμβαδόν να ελαχιστοποιείται.
έτσι ώστε το εμβαδόν να ελαχιστοποιείται. ,
, 


 και έχουμε
και έχουμε ![\displaystyle{E'(\lambda )=0\xrightarrow[\lambda >0]{\lambda (\lambda +1)>0} 2\lambda ^{2} + 2\lambda - 4 = 0 \Leftrightarrow \lambda = 1 \vee \lambda = - 2} \displaystyle{E'(\lambda )=0\xrightarrow[\lambda >0]{\lambda (\lambda +1)>0} 2\lambda ^{2} + 2\lambda - 4 = 0 \Leftrightarrow \lambda = 1 \vee \lambda = - 2}](/forum/ext/geomar/texintegr/latexrender/pictures/c8133483662fd7ea735cb2e588146d65.png)
 οπότε δεκτή είναι μόνο η
οπότε δεκτή είναι μόνο η 


 και έχουμε
και έχουμε
 , τότε το σύστημα έχει μοναδική λύση την
, τότε το σύστημα έχει μοναδική λύση την 
 , τότε το σύστημα γράφεται
, τότε το σύστημα γράφεται

 και αντικαθιστώντας στην τρίτη παίρνουμε,
και αντικαθιστώντας στην τρίτη παίρνουμε, 

 είναι δύο διαφορετικές λύσεις του συστήματος, τότε βρισκόμαστε στην
είναι δύο διαφορετικές λύσεις του συστήματος, τότε βρισκόμαστε στην και
και

 είναι,
είναι,
 και ακτίνας
και ακτίνας 
 ανήκουν στον κύκλο διότι
ανήκουν στον κύκλο διότι  και
και
 είναι μια χορδή του παραπάνω κύκλου και επειδή
είναι μια χορδή του παραπάνω κύκλου και επειδή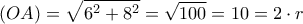 , έπεται ότι το
, έπεται ότι το