Σελίδα 4 από 4
Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ
Δημοσιεύτηκε: Τετ Νοέμ 26, 2014 11:17 pm
από exdx
ΘΕΜΑ 2_17664
( Η λύση του Γ. Λέκκα σε Latex )
Δίνονται οι γωνίες

και

, για τις οποίες ισχύει:

Να αποδείξετε ότι:
α)

(Μονάδες 10)
β)

(Μονάδες 15)
ΛΥΣΗ
α) Είναι

β) Από τον τύπο

και το (α) παίρνουμε:


Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ
Δημοσιεύτηκε: Κυρ Νοέμ 30, 2014 9:47 pm
από rek2
pap65 έγραψε:ΘΕΜΑ 17652
Δίνεται γωνία

που ικανοποιεί τη σχέση:

α) Να αποδείξετε ότι είτε

είτε

. (Μονάδες 13)
β) Να βρείτε τις δυνατές τιμές της γωνίας

. (Μονάδες 12)
ΛΥΣΗ
Α) Είναι



ή

Β) Αν

ή

,

.
Γενικά

,

(Δη λαδή τα ακέραια πολλαπλάσια του

)
Αν

,

.
Γενικά

,

( Το σύνολο των δυνατών τιμών της γωνίας

θα μπορούσε να εκφραστεί γενικά από την σχέση

,

. )
Ας δούμε το σημείο αυτό της εκφώνησης:
α) Να αποδείξετε ότι είτε

είτε

Αυτό το ... "είτε".... " είτε"..., δεν παραπέμπει σε αποκλειστική διάζευξη;
Αν απαντήσουμε ναι, τότε πρέπει να συμπληρωθεί η λύση. Αν απαντήσουμε όχι, τότε τι εξυπηρετεί αυτή η διατύπωση;
Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ
Δημοσιεύτηκε: Κυρ Νοέμ 30, 2014 10:53 pm
από exdx
rek2 έγραψε:pap65 έγραψε:ΘΕΜΑ 17652
Αυτό το ... "είτε".... " είτε"..., δεν παραπέμπει σε αποκλειστική διάζευξη;
Νομίζω ότι είναι ατόπημα της εκφώνησης .
Οι μαθητές , εξάλλου , δεν είναι είναι εξοικειωμένοι πλήρως με την αποκλειστική διάζευξη .
Δεν υπάρχει στο εισαγωγικό κεφάλαιο της Α λυκείου , αλλά μόνο σαν εφαρμογή στις πιθανότητες .
Από την άλλη ο θεματοδότης καλύπτεται από
αυτό
......Αν το "ή", που χρησιμοποιούμε σε μια σύνθετη πρόταση, είναι εγκλειστικό ή αποκλειστικό γίνεται αντιληπτό από το πλαίσιο εντός του οποίου εκφέρεται η πρόταση αυτή.
Υπάρχουν και άλλες λέξεις ή διατάξεις λέξεων που έχουν την ίδια λογική συμπεριφορά με τη λέξη ή, που περιγράφεται από τον ίδιο πίνακα αληθείας, όπως για παράδειγμα η λέξη
είτε. Αυτές μπορεί να έχουν λεπτές σημασιολογικές διαφοροποιήσεις από το σύνδεσμο «...ή...», αλλά έχουν ακριβώς την ίδια λογική συμπεριφορά με αυτόν, η οποία περιγράφεται από τον πίνακα 7. Για το λόγο αυτό θεωρούνται από άποψη λογικής συμπεριφοράς διαζεύξεις .....
Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ
Δημοσιεύτηκε: Δευ Δεκ 01, 2014 10:17 am
από akis_man
Νέα θέματα Άλγεβρας Β Λυκείου από την τράπεζα θεμάτων
GI_V_ALG_2_20329
GI_V_ALG_2_20328
GI_V_ALG_2_19913
Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ
Δημοσιεύτηκε: Δευ Δεκ 01, 2014 11:27 am
από akis_man
ΘΕΜΑ: GI_V_ALG_2_20328
Δίνεται το σύστημα:

, με παράμετρο

.
α) Να αποδείξετε ότι για τις ορίζουσες

του συστήματος ισχύουν:

,

,

(Μονάδες 15)
β) Αν είναι

και

, τότε να λύσετε το σύστημα.
(Μονάδες 10)
ΛΥΣΗ:
α) Οι ορίζουσες είναι:


 β)
β) Για

και

έχουμε ότι

, οπότε το σύστημά μας θα έχει μοναδική λύση

, με

και

.


Άρα

,

.
Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ
Δημοσιεύτηκε: Δευ Δεκ 01, 2014 4:58 pm
από pap65
Ετοιμάζω την 4_20337
Άκυρο. Έχει ήδη γίνει στο σωστό μέρος!
Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ
Δημοσιεύτηκε: Δευ Δεκ 01, 2014 6:02 pm
από ΛΕΚΚΑΣ ΓΙΩΡΓΟΣ
Καλησπέρα σας. Ανεβάζω την 4_20336 σε Word
Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ
Δημοσιεύτηκε: Δευ Δεκ 01, 2014 10:17 pm
από asemarak
GI_V_ALG_2_19913
Έστω η συνάρτηση

,

α) Να αποδείξετε ότι

, για κάθε

Μονάδες 12
β) Να βρείτε την περίοδο καθώς και τη μέγιστη και ελάχιστη τιμή της f. Μονάδες 13
ΛΥΣΗ
α) Για κάθε

:


β) Η συνάρτηση

έχει μέγιστη τιμή

, ελάχιστη τιμή

και περίοδο

,
οπότε και η συνάρτηση

έχει μέγιστη τιμή
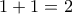
, ελάχιστη τιμή

και περίοδο

.
Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ
Δημοσιεύτηκε: Δευ Δεκ 01, 2014 10:34 pm
από akis_man
Ετοιμάζω την 4_20337
ΛΕΚΚΑΣ ΓΙΩΡΓΟΣ έγραψε:Καλησπέρα σας. Ανεβάζω την 4_20336 σε Word
Κύριε Λέκκα και pap65, αν μου επιτρέπεται, ο χώρος που ανεβάσατε τις λύσεις σας, είναι λάθος, διότι εδώ ανεβαίνουν ασκήσεις από το 2ο θέμα της Άλγεβρας.
Αν μπορείτε να μεταφέρετε την απάντησή σας (με τα αρχεία), στο σωστό σημείο που είναι εδώ:
viewtopic.php?f=147&t=46866&start=40
Σημείωση: Αν και οι ασκήσεις 4_20336 και 4_20337 έχουν λυθεί από τα μέλη george visvikis και Γιώργος Απόκης, δεν πειράζει να τις έχουμε δύο φορές φαντάζομαι...
Ευχαριστώ εκ των προτέρων για τον χρόνο σας...
Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ
Δημοσιεύτηκε: Δευ Δεκ 01, 2014 10:56 pm
από polysot
Ετοιμάζω την GI_V_ALG_2_20329
Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ
Δημοσιεύτηκε: Τρί Δεκ 02, 2014 7:04 am
από ΛΕΚΚΑΣ ΓΙΩΡΓΟΣ
akis_man έγραψε:Ετοιμάζω την 4_20337
ΛΕΚΚΑΣ ΓΙΩΡΓΟΣ έγραψε:Καλησπέρα σας. Ανεβάζω την 4_20336 σε Word
Κύριε Λέκκα και pap65, αν μου επιτρέπεται, ο χώρος που ανεβάσατε τις λύσεις σας, είναι λάθος, διότι εδώ ανεβαίνουν ασκήσεις από το 2ο θέμα της Άλγεβρας.
Αν μπορείτε να μεταφέρετε την απάντησή σας (με τα αρχεία), στο σωστό σημείο που είναι εδώ:
viewtopic.php?f=147&t=46866&start=40
Σημείωση: Αν και οι ασκήσεις 4_20336 και 4_20337 έχουν λυθεί από τα μέλη george visvikis και Γιώργος Απόκης, δεν πειράζει να τις έχουμε δύο φορές φαντάζομαι...
Ευχαριστώ εκ των προτέρων για τον χρόνο σας...
KAΛΗΜΕΡΑ. Έχετε δίκιο, το είδα εκ των υστέρων ότι ήταν σε λάθος σημείο. Επειδή όμως ΌΤΑΝ ΘΈΛΗΣΑ να την μεταφέρω στο 4ο ΑΛΓΕΒΡΑΣ είχε λυθεί, δεν είχε νόημα η μεταφορά.
Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ
Δημοσιεύτηκε: Τρί Δεκ 02, 2014 9:54 am
από Γιώργος Ρίζος
ΛΕΚΚΑΣ ΓΙΩΡΓΟΣ έγραψε:
Ευχαριστώ εκ των προτέρων για τον χρόνο σας...
KAΛΗΜΕΡΑ. Έχετε δίκιο, το είδα εκ των υστέρων ότι ήταν σε λάθος σημείο. Επειδή όμως ΌΤΑΝ ΘΈΛΗΣΑ να την μεταφέρω στο 4ο ΑΛΓΕΒΡΑΣ είχε λυθεί, δεν είχε νόημα η μεταφορά.
Γιώργο καλημέρα. Αν θες, μετάφερε τη λύση σου στη συζήτηση του 4ου θέματος. Ήδη την έχω χρησιμοποιήσει, σε συνδυασμό με την άλλη λύση, στο Δελτίο λύσεων.
Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ
Δημοσιεύτηκε: Τετ Δεκ 03, 2014 11:54 pm
από polysot
20329

- 20329.JPG (31.13 KiB) Προβλήθηκε 5529 φορές
Η

είναι γνησίως φθίνουσα στο
![(-\infty, -2] (-\infty, -2]](/forum/ext/geomar/texintegr/latexrender/pictures/add629699765b31b602c7a1cd0bce7d2.png)
και γνησίως αύξουσα στο

Έχει ολικό ελάχιστο στο

με

.
β) Η

πρέπει να μετατοπιστεί

μονάδες δεξιά και

κάτω, δηλαδή:

.
Ειδικότερα για

έχουμε

.
Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ
Δημοσιεύτηκε: Πέμ Δεκ 04, 2014 2:38 pm
από Γιώργος Απόκης
Μετά από επισήμανση του dimkat, έκανα μια προσθήκη στην άσκηση
17709
Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ
Δημοσιεύτηκε: Σάβ Ιαν 24, 2015 6:31 pm
από exdx
2_22680
Δίνονται τα πολυώνυμα:

και

α) Ένας μαθητής ισχυρίζεται ότι και τα δύο πολυώνυμα είναι 3ου βαθμού.
Συμφωνείτε με την άποψη αυτή; Να δικαιολογήσετε την απάντησή σας. (Μονάδες 13)
β) Να βρείτε την τιμή του

για την οποία τα πολυώνυμα

και

είναι ίσα. (Μονάδες 12)
Λύση
α) Μετά τις πράξεις είναι :

και

Επομένως
Αν

είναι και τα δύο τρίτου βαθμού ενώ αν

είναι και τα δύο δευτέρου βαθμού .
Επομένως ούτε διαφωνώ , ούτε συμφωνώ με την άποψη του μαθητή , αφού άλλοτε είναι σωστή και άλλοτε λάθος .
(Εδώ , λείπει από την εκφώνηση το «για κάθε  » ή το «πάντα» )
» ή το «πάντα» )
β) Πρέπει και αρκεί :

Re: 2o ΘΕΜΑ ΑΛΓΕΒΡΑΣ Β ΛΥΚΕΙΟΥ
Δημοσιεύτηκε: Τετ Ιαν 28, 2015 6:01 pm
από george visvikis
Άσκηση 2_22681
Δίνεται το πολυώνυμο

. Αν το

έχει παράγοντα το

και

, τότε:
α) Να αποδείξετε ότι
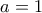
και

(Μονάδες 10)
β) Να λύσετε την εξίσωση:
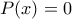
(Μονάδες 8)
γ) Να λύσετε την ανίσωση:

(Μονάδες 7)
Λύση:
α) Από την υπόθεση έχουμε

και

.
Προσθέτουμε κατά μέλη τις δύο τελευταίες εξισώσεις και βρίσκουμε

και αντικαθιστώντας σε μία από τις δύο,

.
β) Η εξίσωση γράφεται


(αφού

για κάθε
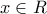
).
γ)

(αφού

για κάθε
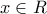
)
...Αν και δεν έχει νόημα αφού καταργείται η Τράπεζα θεμάτων
 και
και  , για τις οποίες ισχύει:
, για τις οποίες ισχύει: 
 (Μονάδες 10)
(Μονάδες 10) (Μονάδες 15)
(Μονάδες 15)
 και το (α) παίρνουμε:
και το (α) παίρνουμε: 

 και
και  , για τις οποίες ισχύει:
, για τις οποίες ισχύει: 
 (Μονάδες 10)
(Μονάδες 10) (Μονάδες 15)
(Μονάδες 15)
 και το (α) παίρνουμε:
και το (α) παίρνουμε: 

 που ικανοποιεί τη σχέση:
που ικανοποιεί τη σχέση:
 είτε
είτε . (Μονάδες 13)
. (Μονάδες 13)

 ή
ή  ή
ή  ,
, .
. ,
,  )
)  ,
, ,
,  ,
,  , με παράμετρο
, με παράμετρο  .
. του συστήματος ισχύουν:
του συστήματος ισχύουν: ,
,  ,
, 
 και
και  , τότε να λύσετε το σύστημα.
, τότε να λύσετε το σύστημα. 


 , οπότε το σύστημά μας θα έχει μοναδική λύση
, οπότε το σύστημά μας θα έχει μοναδική λύση  , με
, με  και
και  .
.

 ,
,  .
. ,
, 
 , για κάθε
, για κάθε 

 έχει μέγιστη τιμή
έχει μέγιστη τιμή  , ελάχιστη τιμή
, ελάχιστη τιμή  και περίοδο
και περίοδο  ,
, έχει μέγιστη τιμή
έχει μέγιστη τιμή 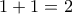 , ελάχιστη τιμή
, ελάχιστη τιμή 
 είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο ![(-\infty, -2] (-\infty, -2]](/forum/ext/geomar/texintegr/latexrender/pictures/add629699765b31b602c7a1cd0bce7d2.png) και γνησίως αύξουσα στο
και γνησίως αύξουσα στο 
 με
με  .
. μονάδες δεξιά και
μονάδες δεξιά και  κάτω, δηλαδή:
κάτω, δηλαδή:  .
. έχουμε
έχουμε  .
. και
και 
 για την οποία τα πολυώνυμα
για την οποία τα πολυώνυμα  και
και  είναι ίσα. (Μονάδες 12)
είναι ίσα. (Μονάδες 12)

 είναι και τα δύο τρίτου βαθμού ενώ αν
είναι και τα δύο τρίτου βαθμού ενώ αν  είναι και τα δύο δευτέρου βαθμού .
είναι και τα δύο δευτέρου βαθμού . » ή το «πάντα» )
» ή το «πάντα» )
 . Αν το
. Αν το  έχει παράγοντα το
έχει παράγοντα το  και
και  , τότε:
, τότε: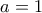 και
και (Μονάδες 10)
(Μονάδες 10)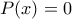 (Μονάδες 8)
(Μονάδες 8) (Μονάδες 7)
(Μονάδες 7) και
και  .
. και αντικαθιστώντας σε μία από τις δύο,
και αντικαθιστώντας σε μία από τις δύο,  .
.
 (αφού
(αφού  για κάθε
για κάθε 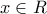 ).
). (αφού
(αφού  για κάθε
για κάθε