ΘΕΜΑ 17842
Δίνεται η συνάρτηση:

με

θετικές σταθερές, η γραφική παράσταση της οποίας διέρχεται από τα σημεία
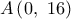
και

.
α) Με βάση τα δεδομένα, να κατασκευάσετε ένα σύστημα δύο εξισώσεων με αγνώστους τους

και να υπολογίσετε την τιμή τους. (Μονάδες 10)
β) Θεωρώντας γνωστό ότι
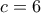
και
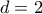
,
i. να βρείτε τα σημεία τομής της γραφικής παράστασης της συνάρτησης

με τους
άξονες. (Μονάδες 3)
ii. να μεταφέρετε στην κόλα σας το σύστημα συντεταγμένων που ακολουθεί, να
σχεδιάσετε τη γραφική παράσταση της συνάρτησης

και να εξηγήσετε πώς αυτή
σχετίζεται με τη γραφική παράσταση της συνάρτησης

(Μονάδες 6)
iii. με βάση την παραπάνω γραφική παράσταση, να βρείτε το ακρότατο της συνάρτησης

, τα διαστήματα στα οποία η

είναι μονότονη, καθώς και το είδος της μονοτονίας της σε καθένα από αυτά τα διαστήματα. (Μονάδες 6 )
ΛΥΣΗ
Α) Η γραφική παράσταση της συνάρτησης

διέρχεται από τα σημεία
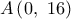
και

, επομένως οι συντεταγμένες των σημείων θα επαληθεύουν την εξίσωσή της .
Δηλαδή

και

Άρα

και

Με αντικατάσταση της σχέσης (1) στην σχέση (2) παίρνουμε:

Αντικαθιστώντας στην σχέση ( 1)

Β) Αφού
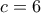
και
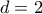
τότε

.
iv. Για να βρούμε τα σημεία τομής της

με τον άξονα
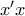
λύνουμε
Το σύστημα

Είναι

Επομένως τα κοινά σημεία της

με τον άξονα
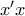
είναι

και

Αντίστοιχα για το σημείο τομής της

με τον άξονα βρίσκουμε το

δηλαδή το δοσμένο σημείο

.
v. Η συνάρτηση

είναι της μορφής

που η γραφική της παράσταση
αποτελεί καμπύλη που την ονομάζουμε παραβολή με κορυφή το σημείο Ο(0,0), το οποίο αποτελεί και το ελάχιστο αυτής.

- 17842.png (45.96 KiB) Προβλήθηκε 11139 φορές
Η γραφική παράσταση της συνάρτησης

αποτελεί μετατόπισης της

, όπως φαίνεται και στο σχήμα ,
κατά

μονάδες στον άξονα

και κατά

μονάδες στον άξονα
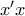
.
vi. Η συνάρτηση

παρουσιάζει ελάχιστο για

που είναι το

.
Στο διάστημα
![\left( -\infty ,6 \right] \left( -\infty ,6 \right]](/forum/ext/geomar/texintegr/latexrender/pictures/a32140f7916af12b197937b2b9ce2b4a.png)
η

είναι γνησίως φθίνουσα.
Στο διάστημα
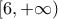
η

είναι γνησίως αύξουσα.
.

 και προαιρετικά μπορεί η δημοσίεση να περιλαμβάνει τη λύση γραμμένη και σε Mathtype.
και προαιρετικά μπορεί η δημοσίεση να περιλαμβάνει τη λύση γραμμένη και σε Mathtype. όπου
όπου  πραγματικές σταθερές.
πραγματικές σταθερές.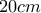 και το μέγιστο είναι
και το μέγιστο είναι  . Τη χρονική στιγμή
. Τη χρονική στιγμή  το ύψος παίρνει την ελάχιστη τιμή του και ο χρόνος μίας πλήρους ταλάντωσης (θέσεις: ελάχιστο - ηρεμία - μέγιστο - ηρεμία ελάχιστο ) είναι
το ύψος παίρνει την ελάχιστη τιμή του και ο χρόνος μίας πλήρους ταλάντωσης (θέσεις: ελάχιστο - ηρεμία - μέγιστο - ηρεμία ελάχιστο ) είναι  .
. (Μονάδες 5)
(Μονάδες 5) μετά την έναρξη της ταλάντωσης. (Μονάδες 8)
μετά την έναρξη της ταλάντωσης. (Μονάδες 8) για
για 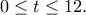 (Μονάδες 6)
(Μονάδες 6) .
. θα ισχύει ότι:
θα ισχύει ότι: 
 , οπότε θα ισχύει ότι:
, οπότε θα ισχύει ότι: 

 είναι περιοδική με περίοδο
είναι περιοδική με περίοδο 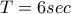 έχουμε:
έχουμε: 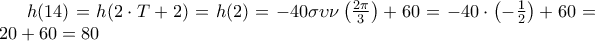
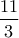 .
. χρόνια.
χρόνια.
 οι ηλικίες πατέρα , μητέρας και παιδιού , αντίστοιχα .
οι ηλικίες πατέρα , μητέρας και παιδιού , αντίστοιχα .

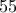 , η μητέρα
, η μητέρα 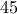 και το παιδί
και το παιδί 
 .
. . (Μονάδες 5)
. (Μονάδες 5) και
και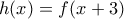 δεν είναι ούτε άρτιες ούτε περιττές . (Μονάδες 5)
δεν είναι ούτε άρτιες ούτε περιττές . (Μονάδες 5)
![\displaystyle{\begin{array}{l}
\,\,A = [ - 8,8] \\
\, \\
\end{array}} \displaystyle{\begin{array}{l}
\,\,A = [ - 8,8] \\
\, \\
\end{array}}](/forum/ext/geomar/texintegr/latexrender/pictures/ac7ae2fef2814bb2763963cbe3adeae6.png)
 και
και 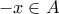 .
.![\displaystyle{x \in [ - 8,8]} \displaystyle{x \in [ - 8,8]}](/forum/ext/geomar/texintegr/latexrender/pictures/a4f886307430512805ff08c8770dcddf.png) , είναι :
, είναι :  , οπότε η
, οπότε η 
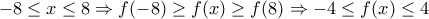 , διότι η
, διότι η 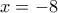 , μέγιστο το
, μέγιστο το  και για
και για  , ελάχιστο το
, ελάχιστο το 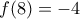
 έχει πεδίο ορισμού επίσης το
έχει πεδίο ορισμού επίσης το ![\displaystyle{A = [ - 8,8]} \displaystyle{A = [ - 8,8]}](/forum/ext/geomar/texintegr/latexrender/pictures/6076cf2009efd292626765c6fdffbc53.png) και η γραφική της παράσταση
και η γραφική της παράσταση  μονάδες προς τα κάτω .
μονάδες προς τα κάτω . . Έτσι δεν είναι συμμετρική ως προς το
. Έτσι δεν είναι συμμετρική ως προς το  , ούτε ως προς τον y΄y άξονα .
, ούτε ως προς τον y΄y άξονα .  έχει τύπο
έχει τύπο  και ορίζεται αν και μόνο αν :
και ορίζεται αν και μόνο αν :
![\displaystyle{{\,D = [ - 11,5]}} \displaystyle{{\,D = [ - 11,5]}}](/forum/ext/geomar/texintegr/latexrender/pictures/b736b3bc517a83dc382de444fe1e0fc9.png) και δεν είναι ούτε άρτια ούτε περιττή αφού δεν ικανοποιείται η συνθήκη :
και δεν είναι ούτε άρτια ούτε περιττή αφού δεν ικανοποιείται η συνθήκη : 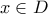 και
και  , αφού π.χ. είναι
, αφού π.χ. είναι  και
και  .
. και
και  με εξισώσεις
με εξισώσεις 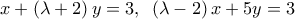 αντίστοιχα με
αντίστοιχα με 

 ενώ έχουμε και
ενώ έχουμε και
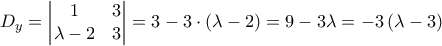
 τότε οι ευθείες τέμνονται σε ένα σημείο Α.
τότε οι ευθείες τέμνονται σε ένα σημείο Α.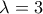 τότε έχουμε, αντικαθιστώντας στο αρχικό μας σύστημα:
τότε έχουμε, αντικαθιστώντας στο αρχικό μας σύστημα:  ,δηλαδή οι ευθείες ταυτίζονται.
,δηλαδή οι ευθείες ταυτίζονται. τότε αντικαθιστώντας στο αρχικό μας σύστημα λαμβάνουμε:
τότε αντικαθιστώντας στο αρχικό μας σύστημα λαμβάνουμε:  επομένως το σύστημα είναι αδύνατο δηλαδή τότε οι ευθείες είναι παράλληλες.
επομένως το σύστημα είναι αδύνατο δηλαδή τότε οι ευθείες είναι παράλληλες. Δηλαδή
Δηλαδή 
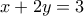 πρέπει και αρκεί οι συντεταγμένες του να επαληθεύουν την εξίσωση της ευθείας. Από το ερώτημα Β έχουμε:
πρέπει και αρκεί οι συντεταγμένες του να επαληθεύουν την εξίσωση της ευθείας. Από το ερώτημα Β έχουμε: 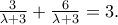


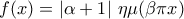 με
με  και
και 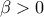 , η οποία έχει μέγιστη τιμή
, η οποία έχει μέγιστη τιμή  .
. ή
ή 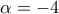 και
και  . (Μονάδες 7)
. (Μονάδες 7) (Μονάδες 10)
(Μονάδες 10)![\displaystyle{\left[ {0\,,\,8} \right]} \displaystyle{\left[ {0\,,\,8} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/7a9a9f1c3ec7e113601cb220b552507c.png) . (Μονάδες 8)
. (Μονάδες 8) , με
, με  και
και 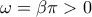 .
.
 ή
ή 
 και
και

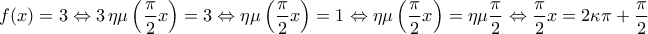

 .
.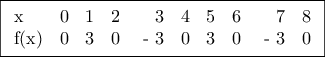
 ισχύει ότι
ισχύει ότι 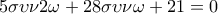 .
.
 , τότε:
, τότε: και
και 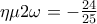 .
.![\Pi = \frac{{13 \cdot \left[ {\eta {\mu ^2}2\omega + \sigma \upsilon {\nu ^2}2\omega } \right] + 12}}{{18 \cdot \varepsilon \varphi 2\omega \cdot \sigma \varphi 2\omega + 25\left[ {\eta \mu 2\omega + \sigma \upsilon \nu 2\omega } \right]}} \Pi = \frac{{13 \cdot \left[ {\eta {\mu ^2}2\omega + \sigma \upsilon {\nu ^2}2\omega } \right] + 12}}{{18 \cdot \varepsilon \varphi 2\omega \cdot \sigma \varphi 2\omega + 25\left[ {\eta \mu 2\omega + \sigma \upsilon \nu 2\omega } \right]}}](/forum/ext/geomar/texintegr/latexrender/pictures/865a82f63623aab750899a528166a077.png)
 (2).
(2).
 με
με ![y \in \left[ { - 1,1} \right] y \in \left[ { - 1,1} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/cf6a8314c97dab267b34126a9aee9635.png) .
.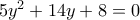 που παριστάνει τριώνυμο με
που παριστάνει τριώνυμο με  και διακρίνουσα
και διακρίνουσα  .
. 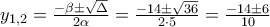 .
. που είναι δεκτή
που είναι δεκτή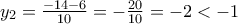 απορρίπτεται.
απορρίπτεται.
 και επομένως η γωνία είναι στο 2ο τεταρτημόριο ενώ η διπλάσια της βρίσκεται στο 3ο ή στο 4ο τεταρτημόριο.
και επομένως η γωνία είναι στο 2ο τεταρτημόριο ενώ η διπλάσια της βρίσκεται στο 3ο ή στο 4ο τεταρτημόριο. 
 .
.

![\displaystyle{\begin{array}{l}
\Pi = \frac{{13 \cdot \left[ {\eta {\mu ^2}2\omega + \sigma \upsilon {\nu ^2}2\omega } \right] + 12}}{{18 \cdot \varepsilon \varphi 2\omega \cdot \sigma \varphi 2\omega + 25\left[ {\eta \mu 2\omega + \sigma \upsilon \nu 2\omega } \right]}} = \frac{{13 \cdot 1 + 12}}{{18 \cdot 1 + 25\left( {\frac{7}{{25}} - \frac{{24}}{{25}}} \right)}} = \\
\frac{{25}}{{18 + 25\left( { - \frac{{17}}{{25}}} \right)}} = \frac{{25}}{{18 - 17}} = 25
\end{array}} \displaystyle{\begin{array}{l}
\Pi = \frac{{13 \cdot \left[ {\eta {\mu ^2}2\omega + \sigma \upsilon {\nu ^2}2\omega } \right] + 12}}{{18 \cdot \varepsilon \varphi 2\omega \cdot \sigma \varphi 2\omega + 25\left[ {\eta \mu 2\omega + \sigma \upsilon \nu 2\omega } \right]}} = \frac{{13 \cdot 1 + 12}}{{18 \cdot 1 + 25\left( {\frac{7}{{25}} - \frac{{24}}{{25}}} \right)}} = \\
\frac{{25}}{{18 + 25\left( { - \frac{{17}}{{25}}} \right)}} = \frac{{25}}{{18 - 17}} = 25
\end{array}}](/forum/ext/geomar/texintegr/latexrender/pictures/51f1083c26b4a34c3a8e31b36669d39d.png)
 , με παράμετρο
, με παράμετρο  .
.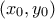 , τότε
, τότε  .
. . (Μονάδες 5)
. (Μονάδες 5)
 και
και , το σύστημα έχει μοναδική λύση την :
, το σύστημα έχει μοναδική λύση την : , οπότε έχουμε άμεσα ότι :
, οπότε έχουμε άμεσα ότι :  , το σύστημα γίνεται :
, το σύστημα γίνεται :

 , το σύστημα γίνεται :
, το σύστημα γίνεται : , το οποίο είναι αδύνατο .
, το οποίο είναι αδύνατο . το σύστημα έχει μοναδική λύση και επομένως οι αντίστοιχες ευθείες έχουν μοναδικό κοινό σημείο , δηλαδή τέμνονται .
το σύστημα έχει μοναδική λύση και επομένως οι αντίστοιχες ευθείες έχουν μοναδικό κοινό σημείο , δηλαδή τέμνονται . , με παράμετρο
, με παράμετρο  .
.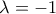 και
και  είναι η αντίστοιχη λύση του συστήματος , να βρείτε γωνία
είναι η αντίστοιχη λύση του συστήματος , να βρείτε γωνία  τέτοια ώστε
τέτοια ώστε  και
και  . (Μονάδες 7)
. (Μονάδες 7) και
και  είναι η αντίστοιχη λύση του συστήματος , να δείξετε ότι δεν υπάρχει γωνία
είναι η αντίστοιχη λύση του συστήματος , να δείξετε ότι δεν υπάρχει γωνία  , τέτοια ώστε
, τέτοια ώστε 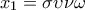 και
και  . (Μονάδες 8)
. (Μονάδες 8)

 Αν
Αν 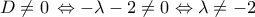 , το
, το 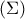 έχει μοναδική λύση το ζεύγος
έχει μοναδική λύση το ζεύγος 
 , τότε:
, τότε:  , προφανώς αδύνατο.
, προφανώς αδύνατο. .
. με
με  και
και  , είναι
, είναι  .
.
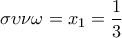 και
και  θα πρέπει:
θα πρέπει:  που είναι άτοπο.
που είναι άτοπο.
 θετικές σταθερές, η γραφική παράσταση της οποίας διέρχεται από τα σημεία
θετικές σταθερές, η γραφική παράσταση της οποίας διέρχεται από τα σημεία 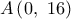 και
και  .
.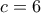 και
και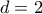 ,
, με τους
με τους (Μονάδες 6)
(Μονάδες 6) και
και 




 .
. με τον άξονα
με τον άξονα 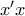 λύνουμε
λύνουμε


 δηλαδή το δοσμένο σημείο
δηλαδή το δοσμένο σημείο  .
. που η γραφική της παράσταση
που η γραφική της παράσταση  αποτελεί μετατόπισης της
αποτελεί μετατόπισης της  , όπως φαίνεται και στο σχήμα ,
, όπως φαίνεται και στο σχήμα ,  μονάδες στον άξονα
μονάδες στον άξονα  και κατά
και κατά  μονάδες στον άξονα
μονάδες στον άξονα  που είναι το
που είναι το  .
.![\left( -\infty ,6 \right] \left( -\infty ,6 \right]](/forum/ext/geomar/texintegr/latexrender/pictures/a32140f7916af12b197937b2b9ce2b4a.png) η
η 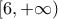 η
η  , με
, με  πραγματικές σταθερές.
πραγματικές σταθερές. της συνάρτησης
της συνάρτησης .
.  και
και , να προσδιορίσετε αλγεβρικά την τετμημένη
, να προσδιορίσετε αλγεβρικά την τετμημένη  του σημείου
του σημείου  και
και 

 είναι θετικοί αριθμοί.
είναι θετικοί αριθμοί. 

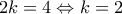
 .
.
 ,
,  .
.  .
.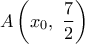 , επομένως οι συντεταγμένες του σημείου θα επαληθεύουν την εξίσωσή της . Δηλαδή
, επομένως οι συντεταγμένες του σημείου θα επαληθεύουν την εξίσωσή της . Δηλαδή  .
.

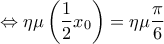
 ή
ή 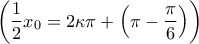
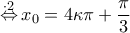 ή
ή 
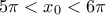
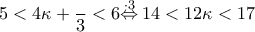
 αδύνατο αφού
αδύνατο αφού 


 έχουμε
έχουμε 

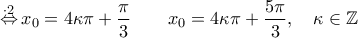
 (Μονάδες 12)
(Μονάδες 12)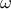 με
με  , που ικανοποιούν τη σχέση
, που ικανοποιούν τη σχέση 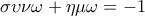

 , ή
, ή 
 ή
ή 
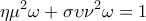 σχηματίζουν το σύστημα :
σχηματίζουν το σύστημα :
 με
με  το σύστημα είναι ισοδύναμο με το :
το σύστημα είναι ισοδύναμο με το :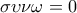 και
και 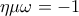 ,κι αφού
,κι αφού  , έχουμε
, έχουμε 
 και
και  κι αφού
κι αφού 


 έως
έως  sec; (Μονάδες 4+2=6)
sec; (Μονάδες 4+2=6) .(Μονάδες 3)
.(Μονάδες 3)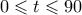 .(Μονάδες 5)
.(Μονάδες 5)
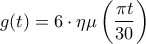 έχουμε ότι:
έχουμε ότι:  και
και  . Συνεπώς
. Συνεπώς και
και  ,δηλαδή το μέγιστο ύψος που φτάνει το κάθισμα είναι
,δηλαδή το μέγιστο ύψος που φτάνει το κάθισμα είναι  και το ελάχιστο
και το ελάχιστο  .
.
 ή
ή  . Όμως
. Όμως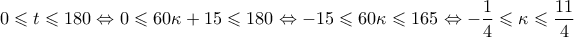 , οπότε
, οπότε ή
ή 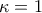 ή
ή  και άρα
και άρα  ή
ή 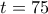 ή
ή 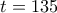 .
.
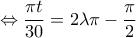 ή
ή 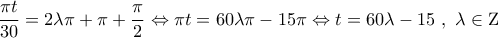 , όμως
, όμως , οπότε
, οπότε ή
ή  ή
ή 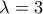 και άρα
και άρα  ή
ή  ή
ή  .
. οπότε η ακτίνα της ρόδας είναι
οπότε η ακτίνα της ρόδας είναι  .
.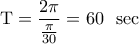 και επομένως οι δύο φίλες έκαναν
και επομένως οι δύο φίλες έκαναν  γύρους.
γύρους.