2_22508
Σε καρτεσιανό επίπεδο

θεωρούμε κύκλο

που διέρχεται από το σημείο

και έχει κέντρο το

.
α) Να αποδείξετε ότι

, και έπειτα να βρείτε την εξίσωση της ευθείας

που διέρχεται από τα σημεία

και

.
(Μονάδες 13)
β) Από τα σημεία του κύκλου

να βρείτε τις συντεταγμένες:
i) του σημείου που απέχει τη μικρότερη απόσταση από την αρχή των αξόνων.
(Μονάδες 6)
ii) του σημείου που απέχει τη μεγαλύτερη απόσταση από την αρχή των αξόνων.
(Μονάδες 6)
ΛΥΣΗ:
α) Ο κύκλος

αφού έχει κέντρο το

, έχει εξίσωση

Αφού διέρχεται από το

, οι συντεταγμένες του

, επαληθεύουν την εξίσωσή του, οπότε

Άρα

Η ευθεία που διέρχεται από τα

έχει συντελεστή διεύθυνσης

και εξίσωση
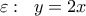

- 27-01-2015 Τράπεζα B Λυκείου.png (14.79 KiB) Προβλήθηκε 5579 φορές
β) Η

τέμνει τον κύκλο στα σημεία με συντεταγμένες που είναι ζεύγη λύσεων του συστήματος
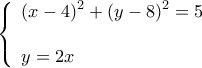
Αντικαθιστώντας την τιμή του

στην πρώτη εξίσωση, έχουμε:
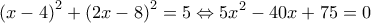

, που έχει ρίζες

και

Οπότε τα σημεία τομής είναι τα

, που απέχει τη μικρότερη απόσταση και το

, που απέχει τη μεγαλύτερη απόσταση από το

.
ΣΧΟΛΙΟ: Δεν απαιτείται η απόδειξη της παραπάνω πρότασης, εφόσον τεκμηριώνεται με την πρόταση που αποδεικνύεται σε άσκηση του βιβλίου Ευκλείδειας Γεωμετρίας Α΄, Β΄ Λυκείου. (η 4 αποδεικτική, παρ 3.12, σελ. 58 ).
Πάντως, εδώ δίνουμε την απόδειξη της ανίσωσης στο παραπάνω θέμα:
Πράγματι, για τυχαίο σημείο

του κύκλου, είναι, από την τριγωνική ανισότητα στο

:



 καθώς και την εξίσωση της ευθείας πάνω στην οποία βρίσκεται αυτό.
καθώς και την εξίσωση της ευθείας πάνω στην οποία βρίσκεται αυτό. 
 έχει συντελεστή
έχει συντελεστή 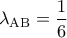 , επομένως η
, επομένως η  ως κάθετη στην
ως κάθετη στην 
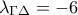 και αφού διέρχεται από το
και αφού διέρχεται από το  θα έχει εξίσωση :
θα έχει εξίσωση :
 είναι ίσο με την απόσταση
είναι ίσο με την απόσταση 
 και
και 
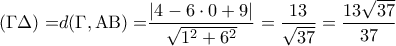

 και προαιρετικά μπορεί η δημοσίεση να περιλαμβάνει τη λύση γραμμένη και σε Mathtype.
και προαιρετικά μπορεί η δημοσίεση να περιλαμβάνει τη λύση γραμμένη και σε Mathtype. ,
,  και
και 
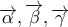 είναι μη συγγραμμικά ανά δύο .
είναι μη συγγραμμικά ανά δύο .  ως γραμμικός συνδυασμός των διανυσμάτων
ως γραμμικός συνδυασμός των διανυσμάτων  και
και  .
. ,
,  και
και  ,
,  και
και  αντίστοιχα.
αντίστοιχα. με
με 


 και
και 
 (1 ) και
(1 ) και  και με αντικατάσταση
και με αντικατάσταση 
 .
. και
και  με
με  και
και  ,
, 

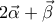 και
και  είναι κάθετα να βρείτε την τιμή του κ.
είναι κάθετα να βρείτε την τιμή του κ.


 .
.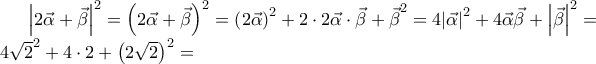


 με τρείς κορυφές τα σημεία
με τρείς κορυφές τα σημεία 
 των διαγωνίων
των διαγωνίων  καθώς και τις συντεταγμένες της κορυφής
καθώς και τις συντεταγμένες της κορυφής 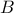 . (Μονάδες 16)
. (Μονάδες 16) .
. 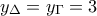 .
.  Οπότε,
Οπότε,  . Συνεπώς
. Συνεπώς  και,
και,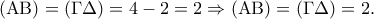
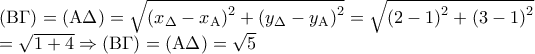
 είναι μέσον του
είναι μέσον του  επομένως οι συντεταγμένες του σημείου είναι:
επομένως οι συντεταγμένες του σημείου είναι: 
 η οποία (από το α))είναι η
η οποία (από το α))είναι η 
 η ευθεία
η ευθεία  . Αφού
. Αφού  , θα είναι της μορφής:
, θα είναι της μορφής: 
 , οπότε η (1)διαμορφώνεται ως εξής:
, οπότε η (1)διαμορφώνεται ως εξής: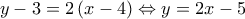 .
.  και
και  .
.  . Άρα
. Άρα 
 και
και  ,
,  για τα οποία ισχύουν:
για τα οποία ισχύουν:  και
και  .
. . (Μονάδες 12)
. (Μονάδες 12) και
και  είναι αντίρροπα και ότι
είναι αντίρροπα και ότι  . (Μονάδες 13)
. (Μονάδες 13)
 .
.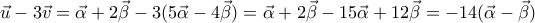
 είναι παράλληλα κι επειδή
είναι παράλληλα κι επειδή  είναι αντίρροπα.
είναι αντίρροπα. .
.  και
και  .
. (1)
(1) και ακτίνα
και ακτίνα 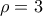 . (Μονάδες 12)
. (Μονάδες 12) , με
, με  ,
,  και
και  .
. . Επομένως η εξίσωση (1) παριστάνει κύκλο με κέντρο
. Επομένως η εξίσωση (1) παριστάνει κύκλο με κέντρο  , δηλαδή
, δηλαδή 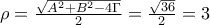 .
.
 , με
, με  ,
,  και
και  .
. δεν εφάπτεται του κύκλου αφού διέρχεται από το κέντρο του.
δεν εφάπτεται του κύκλου αφού διέρχεται από το κέντρο του. έχουν εξίσωση της μορφής
έχουν εξίσωση της μορφής  ,
, 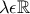 .
.
 ή
ή  .
.  και
και  είναι οι ζητούμενες εφαπτομένες.
είναι οι ζητούμενες εφαπτομένες. θεωρούμε κύκλο
θεωρούμε κύκλο  που διέρχεται από το σημείο
που διέρχεται από το σημείο  και έχει κέντρο το
και έχει κέντρο το  .
. , και έπειτα να βρείτε την εξίσωση της ευθείας
, και έπειτα να βρείτε την εξίσωση της ευθείας  που διέρχεται από τα σημεία
που διέρχεται από τα σημεία  και
και  .
. , έχει εξίσωση
, έχει εξίσωση
 , οι συντεταγμένες του
, οι συντεταγμένες του 
 έχει συντελεστή διεύθυνσης
έχει συντελεστή διεύθυνσης  και εξίσωση
και εξίσωση 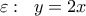
 τέμνει τον κύκλο στα σημεία με συντεταγμένες που είναι ζεύγη λύσεων του συστήματος
τέμνει τον κύκλο στα σημεία με συντεταγμένες που είναι ζεύγη λύσεων του συστήματος 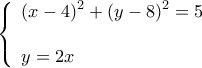
 στην πρώτη εξίσωση, έχουμε:
στην πρώτη εξίσωση, έχουμε: 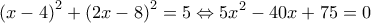
 , που έχει ρίζες
, που έχει ρίζες  και
και 
 , που απέχει τη μικρότερη απόσταση και το
, που απέχει τη μικρότερη απόσταση και το  , που απέχει τη μεγαλύτερη απόσταση από το
, που απέχει τη μεγαλύτερη απόσταση από το  του κύκλου, είναι, από την τριγωνική ανισότητα στο
του κύκλου, είναι, από την τριγωνική ανισότητα στο  :
: 
 και
και 
 και
και  έχουν την ίδια εκκεντρότητα. (Μονάδες 12)
έχουν την ίδια εκκεντρότητα. (Μονάδες 12)  (Μονάδες 13)
(Μονάδες 13)  και
και
 και
και 


 είναι κοινό σημείο των
είναι κοινό σημείο των 
 η έλλειψη
η έλλειψη 

 και την έλλειψη
και την έλλειψη  αντίστοιχα, τότε:
αντίστοιχα, τότε:
 η εξίσωση
η εξίσωση  , επομένως
, επομένως  , άρα
, άρα 
 η εξίσωση
η εξίσωση  , επομένως
, επομένως  , άρα
, άρα 



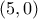
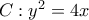 και την κατακόρυφη ευθεία
και την κατακόρυφη ευθεία 
 , όπου
, όπου  είναι η παράμετρος της παραβολής
είναι η παράμετρος της παραβολής  τέμνει την παραβολή
τέμνει την παραβολή  και
και  , τότε:
, τότε: και
και  της παραβολής
της παραβολής  , άρα η εστία είναι
, άρα η εστία είναι 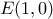 και η διευθετούσα
και η διευθετούσα 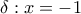
 , έχουμε
, έχουμε  , άρα τα σημεία στα οποία η ευθεία
, άρα τα σημεία στα οποία η ευθεία  και
και  .
. έχει εξίσωση
έχει εξίσωση  . Άρα έχουμε:
. Άρα έχουμε: και
και 
 και
και  , οπότε τέμνονται στο σημείο
, οπότε τέμνονται στο σημείο  , που ανήκει στη διευθετούσα.
, που ανήκει στη διευθετούσα.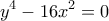 , (1)
, (1) και
και  .
.  είναι οι εστίες των παραβολών
είναι οι εστίες των παραβολών  (Μονάδες 12)
(Μονάδες 12)

 , δηλαδή εστία
, δηλαδή εστία  και διευθετούσα
και διευθετούσα 
 και άξονα συμμετρίας τον
και άξονα συμμετρίας τον  και διευθετούσα
και διευθετούσα 
 με μέσο το
με μέσο το  , οπότε ο κύκλος με διάμετρο το ευθύγραμμο τμήμα
, οπότε ο κύκλος με διάμετρο το ευθύγραμμο τμήμα  .
.